
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные значения и собственные векторы квадратных матрицСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Число Приведенное выше матричное равенство (13) Наличие ненулевого решения Х матричного уравнения Теорема. Собственные значения матрицы суть корни уравнения (14) Если раскрыть этот определитель по правилу вычисления определителей, то получится многочлен степени n относительно Пример. Найти собственные значения матриц: Решение: б) Раздел III. Векторная алгебра и аналитическая геометрия Векторы Все величины, встречающиеся на практике, можно разбить на два класса − скалярные и векторные. Скалярные величины полностью характеризуются задающим их числом (объем, масса, температура, количество студентов в данном ВУЗе, …). Векторные величины характеризуются не только своим численным значением, но и выделенным направлением своего действия (скорость, ускорение, сила…). Вектор – направленный отрезок, у которого обозначены начальная и конечная точки. Обозначение вектора: либо записываются буквы, которыми обозначены начальная и конечная точки вектора, со стрелкой вверху, либо одной буквой со стрелкой, либо одной буквой жирным шрифтом без стрелки: a,
Одной из характеристик вектора является его длина. Векторы
Как видно, некоторые пары коллинеарных векторов направлены в одну сторону, а некоторые − в разные стороны. Коллинеарные векторы Перейдем теперь к понятию равенства двух векторов. Есть несколько различных определений равенства векторов, которые приводят к различным теориям векторов. В зависимости от существа задачи применяются векторы того или иного типа. В теории так называемых жестких векторов два вектора считаются равными, если они совпадают полностью, т.е. если у них совпадают начальные и конечные точки. В теории скользящих векторов можно сдвигать вектор вдоль прямой, на которой он лежит – будут получаться равные векторы. Таким образом, в теории скользящих векторов два вектора будут равными, если они расположены на одной прямой, направлены в одну сторону и имеют одинаковую длину. Например, если груз тянут рукой за привязанную к нему веревку с некоторой силой, направленной вдоль веревки, то характер движения не изменится, если перехватить веревку в другом месте, не меняя величину и направление приложенной силы. Поэтому в этой задаче может быть использована теория скользящих векторов. Мы будем изучать теорию так называемых «свободных» векторов, в которой при переносе вектора параллельно самому себе в любое место пространства будут получаться векторы, равные исходному. При таком переносе сохраняется только длина и направление вектора. Поэтому примем следующее определение. Два вектора называются равными, если они сонаправлены и имеют одинаковую длину. В символьном виде это можно записать так: Следствие. От любой точки пространства можно отложить вектор, равный данному вектору.
Над векторами, оказывается, можно производить некоторые операции, которые мы производим над числами (сложение, вычитание и т. п.). При этом снова будут получаться некоторые векторы. Ниже мы обсудим, по какому правилу эти векторы строятся. Операции над векторами 1. Сумма векторов. Если даны два вектора 1) Правило параллел
Для построения вектора-суммы 2) Правило треугольника. Сложим теперь эти два вектора по правилу треугольника.
Для сложения векторов Если мы построим вектор
3. Умножение числа на вектор. Пусть
Пример. Дан вектор
Как видно из определения, при умножении произвольного ненулевого вектора Теорема. Если Это утверждение часто используется в задачах следующего типа. Требуется найти вектор Вектор Свойства операций над векторами 1. Коммутативность сложения: 2. Ассоциативность сложения: 3. 4. 5. Эти свойства очень похожи на свойства одноименных операций над числами. Первое свойство говорит о том, что векторы можно складывать в любом порядке – будет получаться один и тот же вектор (точнее, два равных вектора – сонаправленные и одной длины). Второе свойство говорит о том, что три вектора можно складывать в любой последовательности. Последние два свойства говорят о том, что при действии с векторами можно раскрывать скобки (или выносить за скобки, если свойство читать справа налево) обычным образом. Эти свойства помогают преобразовывать сложные выражения с векторами механически по привычным правилам (вынесение за скобки, приведение подобных и т.д.). Пример. В Решение. Вектор
Координаты вектора При решении многих математических и практических задач в технических областях часто возникает потребность построения вектора, являющегося достаточно громоздкой комбинацией других векторов, которая включает их многократные сложения, вычитания и умножения на числа. Если выполнять эти операции по их определению, то придется строить соответствующие параллелограммы, треугольники, удлинять и укорачивать вектора, менять их направления и тому подобное. Это достаточно утомительно. Гораздо проще выполнять операции сложения, вычитания и умножения над числами. Нельзя ли заменить одно другим? Этот вопрос касается давней идеи − характеризовать геометрические объекты определенными аналитическими объектами (числами, формулами, алгебраическими выражениями и т.п.), после чего исследование свойств геометрических объектов достаточно громоздкими геометрическими методами можно заменить на определенные манипуляции с этими аналитическими объектами. Первый шаг в этом направлении был сделан, по-видимому, тогда, когда было введено понятие координат точек на плоскости и в пространстве. В этом случае простейший геометрический объект – точка – полностью характеризуется парой (в случае плоскости) или тройкой (в случае пространства) чисел, которые называются координатами этой точки. При этом положение точки однозначно определяет ее координаты и, наоборот, по координатам точки однозначно определяется ее положение. А поскольку единственной характеристикой точки является ее положение в пространстве, то можно сказать, координаты точки полностью ее определяют. Далее введем понятие координат вектора, которые помогут нам достаточно простыми методами исследовать свойства самих векторов и любых их комбинаций. Понятие координат вектора опирается на понятие координат точки, которое будем считать известным.
Теорема. Любой вектор Пример. Найти координаты единичных векторов осей координат Решение. Поскольку эти вектора уже отложены от начала координат, то остается определить координаты их конечных точек, которые (по определению) и будут координатами этих векторов. Глядя на рисунок выше, это несложно сделать: Обозначение координат вектора Оказывается, что координаты вектора полностью определяют все характеристики как самого вектора (длина, направление), так и характер взаимоотношений его с другими векторами (угол, параллельность, перпендикулярность и т.п.). Использование координат вектора значительно облегчает вычисление сложных комбинаций многих векторов, а также решение многих задач, связанных с векторами. Это основано на свойствах координат вектора, приводимых ниже.
Свойства координат вектора Пусть известны координаты вектора 1. Длина вектора определяется по его координатам по следующей формуле: (1) 2. Координаты суммы (разности) векторов получаются сложением (вычитанием) соответствующих координат: (2) 3. При умножении числа на вектор каждая координата умножается на это число: (3) Пример. Даны векторы Как видно из предыдущих свойств и приведенного примера, координаты вектора значительно облегчают операции с ними, позволяя заменить громоздкие геометрические построения обычными действиями с числами. Как же найти координаты вектора? Пока для этого у нас есть только определение. Согласно ему для вычисления координат вектора нужно проделать следующие операции: а) перенести вектор из исходного его положения в начало координат, б) определить координаты конечной точки получившегося вектора. Обе эти операции геометрические, а потому требуют каких-то геометрических построений. Нельзя ли при вычислении координат вектора обойтись без переноса его куда-либо, а использовать исходное положение вектора? Понятно, что можно, иначе этот вопрос даже не озвучивался бы. Но для этого надо знать исходное положение вектора, т.е. положение его начальной и конечной точки. Положение точки определяется ее координатами. Поэтому следующее свойство позволяет по известным координатам начальной и конечной точки вектора находить координаты его самого без тех хлопот, которые предписывает нахождение координат вектора по их определению. 4. Если известны координаты начальной (4) Эти свойства позволяют находить расстояние между точками в пространстве, если определено положение этих точек. Следствие. Расстояние (5) Эта формула легко доказывается, если учесть, что
5. Если (6) Из формулы (1) легко вывести, что для направляющих косинусов всегда выполняется соотношение: Пример. Даны точки Решение. Длина и направляющие косинусы вектора определяются по формулам (1) и (6), которые требуют знания координат вектора. Поэтому прежде всего найдем координаты вектора Как было объявлено выше, координаты должны определять однозначно не только характеристики самого вектора, но и определять взаимное расположение нескольких векторов. Выведем сейчас условие коллинеарности (т.е. параллельности) векторов через соотношения их координат. Пусть векторы Критерий параллельности векторов. Векторы (7) Замечание. Если какие-либо координаты вектора
|
|||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.84.207 (0.011 с.) |

 называется собственным значением квадратной матрицы
называется собственным значением квадратной матрицы  , если существует такой ненулевой n -мерный вектор (т.е. матрица с одним столбцом, не все элементы которой равны нулю)
, если существует такой ненулевой n -мерный вектор (т.е. матрица с одним столбцом, не все элементы которой равны нулю)  , что выполнено:
, что выполнено: 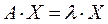 . При этом указанный вектор Х называется собственным вектором матрицы А, отвечающим собственному значению
. При этом указанный вектор Х называется собственным вектором матрицы А, отвечающим собственному значению  .
. . Перенося правые части уравнений в левые части, получим следующую однородную систему уравнений:
. Перенося правые части уравнений в левые части, получим следующую однородную систему уравнений: .
. означает наличие ненулевого решения у однородной системы (13). По Утверждению 2 предыдущего параграфа наличие ненулевого решения однородной системы возможно только в случае, если основной определитель системы равен 0. Таким образом, число
означает наличие ненулевого решения у однородной системы (13). По Утверждению 2 предыдущего параграфа наличие ненулевого решения однородной системы возможно только в случае, если основной определитель системы равен 0. Таким образом, число  .
. . Этот многочлен называется характеристическим многочленом матрицы А. Таким образом, собственные значения матрицы являются корнями ее характеристического многочлена.
. Этот многочлен называется характеристическим многочленом матрицы А. Таким образом, собственные значения матрицы являются корнями ее характеристического многочлена.
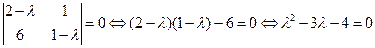 , откуда
, откуда 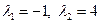 .
. , откуда
, откуда  .
.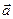 ,
,  . На рисунке изображены некоторые векторы вместе с их обозначением. Векторы, естественно, нарисованы в плоскости страницы, но в принципе их начальные и конечные точки могут располагаться в любом месте трехмерного пространства.
. На рисунке изображены некоторые векторы вместе с их обозначением. Векторы, естественно, нарисованы в плоскости страницы, но в принципе их начальные и конечные точки могут располагаться в любом месте трехмерного пространства.

 Длиной (или модулем) вектора
Длиной (или модулем) вектора  называется длина отрезка АВ. Обозначение длины вектора: |
называется длина отрезка АВ. Обозначение длины вектора: | 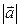 .
.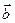 называются коллинеарными (или параллельными), если они расположены на параллельных прямых или на одной прямой. Обозначение коллинеарности векторов:
называются коллинеарными (или параллельными), если они расположены на параллельных прямых или на одной прямой. Обозначение коллинеарности векторов:  ,
, 

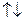
 . Из такого определения равенства векторов следует важный вывод, который в дальнейшем будем использовать.
. Из такого определения равенства векторов следует важный вывод, который в дальнейшем будем использовать.
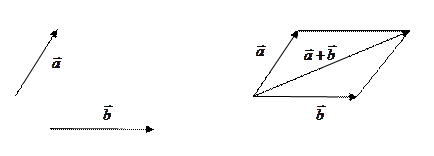 ограмма. Даны два вектора
ограмма. Даны два вектора 

 2. Разность векторов:
2. Разность векторов: 
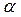 - число,
- число,  на вектор
на вектор  . Для того, чтобы полностью определить вектор, достаточно указать его длину (модуль) и направление. Определим эти характеристики для вектора
. Для того, чтобы полностью определить вектор, достаточно указать его длину (модуль) и направление. Определим эти характеристики для вектора 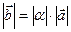 б) если
б) если 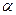 > 0, то
> 0, то 
 Построить векторы
Построить векторы  и
и  .
. , а затем
, а затем  . Найдем длину и направление вектора
. Найдем длину и направление вектора  . Поскольку
. Поскольку 
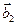 число
число  . Поскольку
. Поскольку 
 на различные числа
на различные числа  все время будут получаться векторы, параллельные вектору
все время будут получаться векторы, параллельные вектору 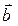 , параллельный вектору
, параллельный вектору  , причем
, причем  , то существует такое число
, то существует такое число  и удовлетворяющий некоторым дополнительным условиям. Тогда понятно, что искомый вектор надо искать в виде
и удовлетворяющий некоторым дополнительным условиям. Тогда понятно, что искомый вектор надо искать в виде 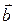 наз. противоположным вектору
наз. противоположным вектору  , если
, если  . Противоположный вектор обозначается:
. Противоположный вектор обозначается:  . Для получения противоположного вектора нужно поменять местами начальную и конечную точки вектора:
. Для получения противоположного вектора нужно поменять местами начальную и конечную точки вектора:  . Действительно, сложив векторы
. Действительно, сложив векторы  , например, по правилу треугольника, получим
, например, по правилу треугольника, получим  . Выполнено естественное равенство:
. Выполнено естественное равенство:  . Действительно, легко по определению проверить, что умножение числа
. Действительно, легко по определению проверить, что умножение числа 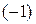 на вектор тоже сводится к смене местами начальной и конечной точки вектора.
на вектор тоже сводится к смене местами начальной и конечной точки вектора. .
.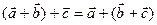 .
.


 даны векторы
даны векторы 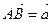 и
и  . Выразить через них векторы
. Выразить через них векторы 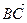 ,
, 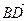 ,
, 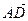 , где
, где 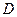 − середина стороны
− середина стороны 
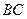 .
. , исходящих из одной и той же точки
, исходящих из одной и той же точки  . Тогда по определению разности векторов вектор
. Тогда по определению разности векторов вектор  . Поскольку вектор
. Поскольку вектор 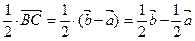 . По правилу треугольника
. По правилу треугольника  .
. Координатами вектора
Координатами вектора  называются координаты конечной его точки, если сам вектор отложить от начала координат (см. рисунок). По этому определению для нахождения координат произвольного вектора
называются координаты конечной его точки, если сам вектор отложить от начала координат (см. рисунок). По этому определению для нахождения координат произвольного вектора  ,
,  и
и 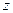 конечной точки
конечной точки 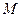
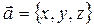 . Таким образом, выражение
. Таким образом, выражение 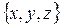 обозначает вектор с координатами
обозначает вектор с координатами  Векторов, конечно же, существует бесчисленное множество. Однако их исследование облегчает тот замечательный факт, что существует тройка таких фиксированных векторов, что любой вектор может быть однозначно представлен в виде линейной комбинации этих трех векторов (под линейной комбинацией векторов понимается сумма этих векторов с какими-либо числовыми коэффициентами перед ними). Любая тройка векторов в пространстве, обладающая таким свойством, называется базисом в пространстве. В качестве такого базиса могут быть взяты, например, так называемые единичные векторы осей координат. Единичные векторы осей координат (орты) – векторы длины 1, направленные по осям координат и имеющие обозначение
Векторов, конечно же, существует бесчисленное множество. Однако их исследование облегчает тот замечательный факт, что существует тройка таких фиксированных векторов, что любой вектор может быть однозначно представлен в виде линейной комбинации этих трех векторов (под линейной комбинацией векторов понимается сумма этих векторов с какими-либо числовыми коэффициентами перед ними). Любая тройка векторов в пространстве, обладающая таким свойством, называется базисом в пространстве. В качестве такого базиса могут быть взяты, например, так называемые единичные векторы осей координат. Единичные векторы осей координат (орты) – векторы длины 1, направленные по осям координат и имеющие обозначение  и
и  (см. рисунок). Оказывается, что любой вектор действительно может быть представлен в виде линейной комбинации векторов
(см. рисунок). Оказывается, что любой вектор действительно может быть представлен в виде линейной комбинации векторов  и
и 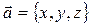 единственным образом представляется в виде линейной комбинации ортов:
единственным образом представляется в виде линейной комбинации ортов: 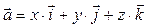 . Обратно, если вектор
. Обратно, если вектор 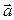 представим в виде
представим в виде  и
и  .
. ,
,  .
.
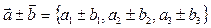

 . Найти длину и координаты вектора
. Найти длину и координаты вектора  .
.  . По формуле (2):
. По формуле (2): 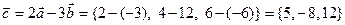 . Наконец, по формуле (1):
. Наконец, по формуле (1):  .
.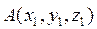 и конечной
и конечной  точек вектора
точек вектора 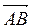 , то координаты самого вектора вычисляются по формуле:
, то координаты самого вектора вычисляются по формуле: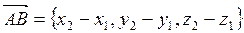
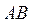 между двумя точками
между двумя точками 
 .
.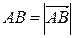 , также формулы (4) и (1).
, также формулы (4) и (1). Первое свойство определяет модуль вектора по его координатам, хотя было обещано, что координаты определяют однозначно все характеристики вектора. Кроме длины, вектор характеризуется и определенным направлением в пространстве. Как же по координатам вектора найти его направление? Для этого нужно сначала договориться, какими величинами может быть определено направление вектора. В качестве таковых могут быть выбраны углы
Первое свойство определяет модуль вектора по его координатам, хотя было обещано, что координаты определяют однозначно все характеристики вектора. Кроме длины, вектор характеризуется и определенным направлением в пространстве. Как же по координатам вектора найти его направление? Для этого нужно сначала договориться, какими величинами может быть определено направление вектора. В качестве таковых могут быть выбраны углы  и
и 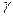 , которые вектор (отложенный от начала координат) составляет с осями координат (см. рисунок). По координатам вектора определяются не сами углы
, которые вектор (отложенный от начала координат) составляет с осями координат (см. рисунок). По координатам вектора определяются не сами углы  , то направляющие косинусы вектора
, то направляющие косинусы вектора  вычисляются по его координатам по формулам:
вычисляются по его координатам по формулам: ,
,  ,
,  .
. .
.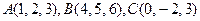 . Найти длину и направляющие косинусы вектора
. Найти длину и направляющие косинусы вектора 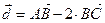 .
. . Для начала по формуле (4) найдем координаты векторов
. Для начала по формуле (4) найдем координаты векторов 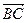 , поскольку известны координаты их конечных и начальных точек:
, поскольку известны координаты их конечных и начальных точек:  ,
,  . Далее, по формуле (3) найдем координаты вектора
. Далее, по формуле (3) найдем координаты вектора 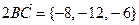 . Наконец, по формуле (2) находим координаты искомого вектора
. Наконец, по формуле (2) находим координаты искомого вектора  . Теперь по формуле (1) длина вектора
. Теперь по формуле (1) длина вектора 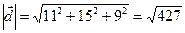 . Теперь, зная координаты и длину вектора
. Теперь, зная координаты и длину вектора 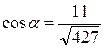 ,
,  ,
,  .
.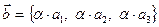 . С другой стороны тот же вектор
. С другой стороны тот же вектор 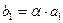 ,
,  и
и  . Отсюда следует, что
. Отсюда следует, что 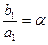 ,
, 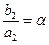 и
и 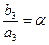 , а потому отношения координат коллинеарных векторов одинаковы. Отсюда следует
, а потому отношения координат коллинеарных векторов одинаковы. Отсюда следует

 .
.


