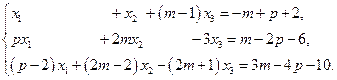Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные значения и собственные векторы матрицыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Комплексное число
Вектор Такой собственный вектор – не единственный, т.к., если
Матричное уравнение (13) эквивалентно однородной системе
Для того чтобы система (14) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю:
Уравнение (15) называется характеристическим для матрицы Если матрица
с разными числами по диагонали ( Как известно из курса алгебры (см, например, ►Пример 14. Найти собственные числа матрицы Решение. Составим характеристическое уравнение
Вычисляем определитель
Уравнение Для того чтобы найти собственный вектор, соответствующий собственному числу ►Пример 15. Найти собственные векторыдля матрицы Решение. Найдем собственный вектор для числа Ранг матрицы этой системы равен двум, на единицу меньше числа неизвестных. Решение найдем через миноры матрицы
Итак, собственный вектор имеет вид Аналогично находятся два других вектора. Советуем студентам найти их самостоятельно. ◄ Упражнения. Найти собственные числа, и для действительных собственных чисел найти собственные векторы матриц: 1) Ответы: 1) 2) 3) 4) 5) 6) 7)
Индивидуальное задание
1. Вычислить определители:
2. Даны матрицы:
Вычислить: a) b)
3. Решить матричное уравнение (найти матрицу
4. Решить системы уравнений двумя способами: по формулам Крамера и с помощью обратной матрицы. а)
5. Исследовать системы уравнений и найти решение, если оно существует. а)
б)
в)
6. Исследовать и решить системы уравнений. а)
б)
в) Приложение В приложении приведены примеры работы с матрицами и примеры решения систем с использованием математического пакета MATHEMATICA Первоначально студент должен ознакомиться с работой интерфейса. Для любой работы необходимо знать операции ввода, вывода результатов; команды для выполнения операций. Ввод данных осуществляется через знак «=». Программа подтверждает ввод строкой «In[1]:=…». Результат выполнения операции находится в строке, начинающейся словом «Out[1]=». Номера в квадратных скобках ввода и вывода совпадают. Выполнение любой операции происходит по команде со строгим выполнением заданного формата. Найти эти форматы можно в справке VIRTUAL BOOK. Там же приведены примеры выполнения операций. Ниже приведен ряд команд для выполнения заданий по теме.
Ввод матрицы. In[4]:= m1 = {{2, -5, 4}, {3, -1, 8}, {2, 6, 1}, {-1, 3, 4}} Имя матрицы m1. Сама матрица вводится построчно с использование фигурных скобок.
Умножение матриц. Команда для умножении «.».
Вычисление определителя. In[10]:= Det[m2] Матрица m2 введена выше.
Нахождение обратной матрицы.
m4 = {{2, 1}, {8, 7}, {3, -5}, {-4, 6}}
Определение ранга матрицы. In[18]:= MatrixRank[m1]
В этом примере система имеет единственное решение. Вместо знака равенства в ответе используется «->». Ниже система, имеющая множество решений и система, не имеющая решений.
Наряду со строчной записью ввода вывода использоваться записью матриц и других математических объектов в привычном виде. Для этого можно использовать команду TraditionalForm
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

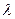 называется собственным числом квадратной матрицы
называется собственным числом квадратной матрицы  , если существует ненулевой вектор (матрица-столбец)
, если существует ненулевой вектор (матрица-столбец)  , такой, что выполнено равенство
, такой, что выполнено равенство . (13)
. (13) - тоже удовлетворяет, где t – любое число, не равное нулю. Следовательно, собственный вектор определяется с точностью до множителя.
- тоже удовлетворяет, где t – любое число, не равное нулю. Следовательно, собственный вектор определяется с точностью до множителя. (14)
(14) (15)
(15) - ой степени относительно
- ой степени относительно  , (16)
, (16) ), то собственные числа совпадают с диагональными элементами матрицы
), то собственные числа совпадают с диагональными элементами матрицы  ), уравнение (15) имеет, по крайней мере, один корень, а пример с матрицей (16) показывает, что у матрицы размера
), уравнение (15) имеет, по крайней мере, один корень, а пример с матрицей (16) показывает, что у матрицы размера  максимум
максимум  .
. .
.
 имеет три действительных корня:
имеет три действительных корня:  , которые и являются собственными числами. ◄
, которые и являются собственными числами. ◄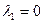 . Для этого решим однородную систему
. Для этого решим однородную систему 
 :
:
 , где
, где  любое число, не равное нулю. Ответ можно писать при t =1, помня замечание, приведенное выше.
любое число, не равное нулю. Ответ можно писать при t =1, помня замечание, приведенное выше.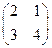 , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  , 6)
, 6) 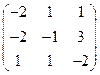 , 7)
, 7) 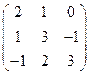 .
. ;
; ;
; ;
; ;
; ;
; ;
; .
. ,
,  ,
,  .
. ,
, 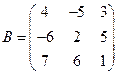 ,
,  ,
,  .
. , где
, где  - единичная матрица.
- единичная матрица. (вычисления проводить, сохраняя три знака после запятой).
(вычисления проводить, сохраняя три знака после запятой). .
. б)
б)