
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема (Кронекера-Капелли).Содержание книги Поиск на нашем сайте Для совместности системы линейных уравнений необходимо и достаточно, чтобы ранг ее основной матрицы ( Пусть Следствие 1. Если ранг матрицы Следствие 2. Если ранг матрицы Метод Гаусса (исключение неизвестных) состоит в том, что с помощью умножения уравнений на ненулевые числа и сложения в первом уравнении оставляем все неизвестные, во втором на одно меньше, в третьем на два меньше и т.д. Эту операцию (назовем ее процедурой Гаусса) удобно проводить, используя матрицы. Составим расширенную матрицу систему и отделим для удобства свободные члены вертикальной линией. С помощью элементарных преобразований приводим матрицу к треугольному виду. Элементарные преобразования матрицы проводим только для строк. Умножая первую строку на соответствующие коэффициенты и прибавляя к лежащим ниже строкам, получим нули в первом столбце. Затем проделываем такую же процедуру со второй строкой, третьей и т.д., до предпоследней строки. В результате преобразований получаем матрицу, по которой можно записать систему, равносильную исходной. Рассмотрим три ситуации, возникающие при исследовании линейных систем. 1) ►Пример 10. Решить систему уравнений методом Гаусса.
Решение. Составим расширенную матрицу и преобразуем ее
Для удобства вычислений переставим четвертую строку на место второй и за счет второй строки получим нули во втором столбце во всех строках ниже второй, а затем за счет третьей строки - в третьем столбце.
В четвертой строке легко было получить нули, умножив третью строку на минус единицу и прибавив ее к четвертой. Мы не упрощали вычислений, чтобы сохранить алгоритм получения нулей в нижележащих строках за один шаг. По преобразованной матрице определяем ранги: . Ответ: система не имеет решений. ◄
2) ►Пример 11. Решить систему уравнений методом Гаусса
Решение.
Ранг основной матрицы равен рангу расширенной матрицы
Полученная система имеет ступенчатый вид и легко решается. Ответ:
3) Рассмотрим запись решения таких систем в матричной форме. Пусть дана система
и известно, что
Минор
Решая эту систему по методу Крамера, имеем
где
Символ:
Тогда множество решений системы можно записать в виде
Для вычисления . Выбор свободных неизвестных, вообще говоря, можно делать по-разному. Однако не всякие ►Пример 12. Решить систему уравнений
Решение. Преобразуем расширенную матрицу системы
Ранг основной матрицы равен рангу расширенной матрицы
Ответ запишем в виде вектора-столбца. Ответ: Получим также решение заданной системы, используя формулу (11). Положим
Положим
Положим
Окончательное решение: Упражнения. Исследовать и решить системы уравнений. 1.
2.
3.
4.
5.
6. 7. 8. 9.
10.
Однородные системы
Система однородных уравнений всегда совместна. Если ранг матрицы коэффициентов равен числу неизвестных, то система имеет единственное нулевое (тривиальное) решение. Если ранг матрицы однородной системы на единицу меньше числа неизвестных, то система имеет одну степень свободы, и ее решение можно записать через миноры матрицы коэффициентов. Для этого в матрице коэффициентов необходимо оставить Так для системы двух линейных однородных уравнений с тремя неизвестными
решение имеет вид
►Пример 13. Решить систему
Решение. Матрица коэффициентов
Ответ запишем в виде вектора Упражнения. Решить системы. 1) Ответы: 1)
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2066; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 ) был равен рангу расширенной матрицы (
) был равен рангу расширенной матрицы ( ).
). . Тогда верны следующие утверждения.
. Тогда верны следующие утверждения. , то система имеет единственное решение.
, то система имеет единственное решение. неизвестных, которые называются свободными, принимают произвольные значения. Говорят, что система имеет
неизвестных, которые называются свободными, принимают произвольные значения. Говорят, что система имеет  . Система несовместна.
. Система несовместна.
 .
.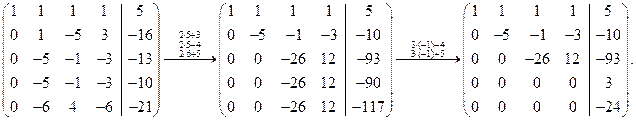
 ,
,  , следовательно, данная система уравнений несовместна.
, следовательно, данная система уравнений несовместна. . Система совместна и имеет единственное решение. В результате преобразований приходим к ступенчатой системе, решение которой легко находится.
. Система совместна и имеет единственное решение. В результате преобразований приходим к ступенчатой системе, решение которой легко находится.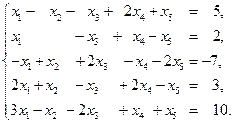

 и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение. По преобразованной матрице составляем систему, равносильную исходной
и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение. По преобразованной матрице составляем систему, равносильную исходной
 .◄
.◄ . Система совместна, но имеет бесконечное множество решений. Это множество решений находим, перенося члены со свободными неизвестными в правую часть уравнений.
. Система совместна, но имеет бесконечное множество решений. Это множество решений находим, перенося члены со свободными неизвестными в правую часть уравнений.
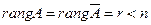 . Тогда система имеет
. Тогда система имеет  :
: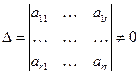 .
. , поэтому строки с номерами
, поэтому строки с номерами  являются линейными комбинациями первых
являются линейными комбинациями первых 
 ,
,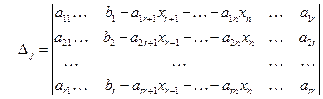 - определитель, полученный из базисного заменой
- определитель, полученный из базисного заменой  го столбца на столбец правой части системы. Пользуясь свойствами определителей, имеем
го столбца на столбец правой части системы. Пользуясь свойствами определителей, имеем . (11)
. (11) ,- означает, что
,- означает, что  . Вектор
. Вектор 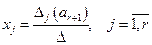 , является решением системы, Главный определитель системы совпадает с базисным минором, а свободные члены равны коэффициентам при неизвестном
, является решением системы, Главный определитель системы совпадает с базисным минором, а свободные члены равны коэффициентам при неизвестном  .
. (12)
(12) полагаем свободные неизвестные равными нулю. Для вычисления
полагаем свободные неизвестные равными нулю. Для вычисления  полагаем свободные члены равными нулю,
полагаем свободные члены равными нулю,  , а остальные свободные неизвестные равными нулю.
, а остальные свободные неизвестные равными нулю.

 .
. , но меньше числа неизвестных. Следовательно, система совместна, но имеет бесконечное множество решений. Число степеней свободы равно двум. Выберем свободными неизвестными
, но меньше числа неизвестных. Следовательно, система совместна, но имеет бесконечное множество решений. Число степеней свободы равно двум. Выберем свободными неизвестными  и выразим
и выразим 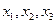 через них.
через них.
 отсюда получаем
отсюда получаем 
 . ◄
. ◄ .
.  Получаем вектор
Получаем вектор  .
. .
. Получаем вектор
Получаем вектор  .
. .
.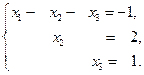 Получаем вектор
Получаем вектор  .
. ◄
◄ Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  линейно независимых строк, а затем вычислить миноры, поочередно вычеркивая столбцы и изменяя знак при каждом переходе.
линейно независимых строк, а затем вычислить миноры, поочередно вычеркивая столбцы и изменяя знак при каждом переходе.
 , где
, где  принимает любое значение.
принимает любое значение.
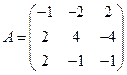 . Определитель
. Определитель  Минор
Минор  Следовательно, ранг матрицы коэффициентов равен двум и на единицу меньше числа неизвестных. Оставив две линейно независимых строки в матрице
Следовательно, ранг матрицы коэффициентов равен двум и на единицу меньше числа неизвестных. Оставив две линейно независимых строки в матрице 
 , получаем
, получаем .
. . ◄
. ◄ 2)
2) 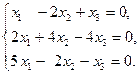 3)
3) 
 ; 2)
; 2)  ; 3)
; 3)  ;
;  .
.


