
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы и действия с матрицами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введение Настоящее пособие предназначено для знакомства с основами линейной алгебры и содержит разделы, посвященные теории матриц и теории систем линейных уравнений. Оно предназначено студентам 1-го курса и может быть полезно всем, кого интересует простое и компактное изучение материала. В каждом параграфе, кроме краткого изложения теории, содержатся примеры с решениями и упражнения для самостоятельного решения. Приведены также типовые индивидуальные задания. Нумерация формул и рисунков в пособии сквозная. Ключевые слова в определениях и формулировках утверждений выделены курсивом. С развитием компьютерной техники появилась возможность решать многие задачи линейной алгебры, не очень доступные в недалеком прошлом ввиду сложности вычислений. Как известно, для решения математических задач существует много различных программных пакетов. Универсальным пакетом является пакет MATHEMATICA. Примеры вычислений в пакете MATHEMATICA в приложении. Освоив предложенные в пособии методы вручную, рекомендуем проделать вычисления с использованием компьютера.
Литература.
1. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1977. 2. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. – СПб.: Издательство «Лань», 1998. 3. Краснов М.Л., Киселев А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И., Соболев С.К. Вся высшая математика: Учебник. Т. 1. – М.: Эдиториал УРСС, 2000. 4. Данко П.Е, Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.: Высшая школа, 1999. Ч.1.- 304 с. - Ч.2. - 416 с. 5. Фридман Г. Н., Леора С.Н. Математика & Mathematica. Избранные задачи для избранных студентов. – Невский Диалект, БХВ-Петербург, 2010, 299 с.
Упражнения. Даны матрицы: Выполнить действия: 1) Ответы: 1)
6. Вычислить 7. Найти 8. Вычислить
Определители
Определителем (детерминантом) n -го порядка называется числовая характеристика квадратной матрицы A размера Определитель первого порядка – определитель для матрицы размера
Минором В общем случае минором прямоугольной матрицы называется любой определитель, полученный из нее в результате вычеркивания каких-то строк или столбцов. Алгебраическим дополнением к элементу
Для вычисления определителя
или
Формулы (1)-(2) представляют разложение определителя по элементам строки (столбца) и в частности показывают, что определитель не изменяется при перестановке строк со столбцами, т.е. определители исходной матрицы и транспонированной к ней равны. Для определителей второго и третьего порядков тогда имеем:
При вычислении определителя третьего порядка удобно пользоваться следующей схемой (схема Саррюса):
Определитель равен алгебраической сумме произведений элементов, соединенных одной непрерывной линией. Для определителей порядка выше третьего подобных схем не составлено.
Свойства определителей. Так как определитель не меняется при транспонировании матрицы, свойства, приведенные ниже для строк, справедливы и для столбцов. 1. Определитель, имеющий нулевую строку равен нулю. 2. Определитель, у которого две строки равны или пропорциональны, равен нулю. 3. Общий множитель строки можно выносить за знак определителя. 4. Перестановка двух строк определителя изменяет знак определителя. 5. Если строку определителя умножить на постоянное число и прибавить к другой строке, то определитель не изменится. 6. Сумма произведений элементов строки на соответствующие алгебраические дополнения к элементам другой строки равна нулю. 7. Определитель можно представить в виде суммы определителей согласно формуле
8. Определитель То есть определитель треугольной матрицы равен произведению ее диагональных элементов. 9. Определитель произведения квадратных матриц равен произведению определителей этих матриц: ►Пример 2. Разложить по элементам третьей строки и вычислить определитель
Решение. Воспользуемся формулой (1), а определители третьего порядка вычислим по схеме Саррюса
►Пример 3. Решить уравнение Решение. По формуле (3) раскроем определитель, а затем решим уравнение
►Пример 4. Найти определитель Решение. Все столбцы, начиная со второго, прибавим к первому столбцу, вынесем общий множитель из вновь полученного первого столбца, а затем первую строку вычтем из всех остальных
Упражнения.
1. Вычислить определители. а) д) и) Ответы: а) -12; б)29; в)87; г) 2. Найти значение 3. Найти положительное значение 4. Доказать: а) в)
5. Упростить определитель, разложив его на слагаемые Ответ: 6. Вычислить определители. а) в) Ответы: а) -1487600; б) -29 400 000; в)
7. Найти сумму всех алгебраических дополнений определителя 8. Известно, что числа 20604, 53227, 25755, 20927, 289 делятся на 17. Не вычисляя определителя 9. Пусть
Упражнения. 1. Для заданных матриц найти обратную матрицу. а) Ответы: а) д) 2. Найти неизвестную матрицу из уравнений.
а)
г)
Ответы: а)
Ранг матрицы
Рангом матрицы К элементарным преобразованиям матрицы относятся: - транспонирование; - удаление или добавление строки (столбца), состоящей из нулей; - умножение строки (столбца) на число, отличное от нуля; - перестановка строк (столбцов); -прибавление к элементам какой-либо строки элементов другой строки, умноженных на постоянное число (тоже для столбцов). Выполняя элементарные преобразования над матрицей, получаем другую матрицу, называемую эквивалентной. Переход от исходной матрицы к эквивалентной обычно обозначается символом Используя перечисленные действия, матрицу можно преобразовать к треугольному виду, что позволяет легко определить ее ранг.
►Пример 7. Найти ранг матрицы Решение.
Минор При преобразовании матрицы мы проводили операции только со строками и по определенному алгоритму. Этот метод стандартный, но не является обязательным. С рангом матрицы связано понятие линейно зависимых (независимых) векторов. Пусть в пространстве
Линейной комбинацией векторов
где Если Векторы Векторы Если система из Ранг матрицы определяет наибольшее число линейно независимых строк (столбцов), рассматриваемых как векторы. Так в матрице
Матрица
Упражнения. 1. Найти ранг матриц: а) г) 2. Для матрицы примера 7 получить линейную комбинацию первых трех строк, равную пятой строке. Ответ:
Системы линейных уравнений. Основные понятия.
Системой
где Линейная система называется однородно й, если все свободные члены равны нулю.
В противном случае линейная система называется неоднородной. Решением системы (7) называется упорядоченная совокупность
при подстановке которых вместо Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения, - несовместной. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Однородная система (8) всегда совместна, так как она имеет очевидное решение: Две системы называются равносильными или эквивалентными, если любое решение одной из них является также решением и другой, и обратно, т.е. они имеют одно и то же множество решений. В частности, любые две несовместные системы являются эквивалентными. Линейную систему можно записать в матричной форме. Введем матрицы
Тогда систему (7) можно записать в виде матричного уравнения
а решение (9) в виде матрицы-столбца
Матрица коэффициентов
называется основной матрицей системы. Матрица, составленная из коэффициентов и свободных членов,
называется расширенной матрицей системы. Выражение «решить систему» означает: выяснить, совместна или несовместна система, а в случае совместности – найти все ее решения.
Теорема Крамера.
Дана система, в которой число уравнений совпадает с числом неизвестных
Определитель, составленный из коэффициентов системы
называется главным определителем системы. Если главный определитель системы не равен нулю, то система имеет единственное решение и
Определители
►Пример 8. По формулам Крамера найти решение системы уравнений Решение. Вычислим определители и найдем решение
Ответ: Упражнения. Решить системы по формулам Крамера. 1) Ответы: 1)
Упражнения. Найти решение систем с помощью обратной матрицы.
а) г)
Упражнения. Исследовать и решить системы уравнений. 1.
2.
3.
4.
5.
6. 7. 8. 9.
10.
Однородные системы
Система однородных уравнений всегда совместна. Если ранг матрицы коэффициентов равен числу неизвестных, то система имеет единственное нулевое (тривиальное) решение. Если ранг матрицы однородной системы на единицу меньше числа неизвестных, то система имеет одну степень свободы, и ее решение можно записать через миноры матрицы коэффициентов. Для этого в матрице коэффициентов необходимо оставить Так для системы двух линейных однородных уравнений с тремя неизвестными
решение имеет вид
►Пример 13. Решить систему
Решение. Матрица коэффициентов
Ответ запишем в виде вектора Упражнения. Решить системы. 1) Ответы: 1)
Упражнения. Найти собственные числа, и для действительных собственных чисел найти собственные векторы матриц: 1) Ответы: 1) 2) 3) 4) 5) 6) 7)
Индивидуальное задание
1. Вычислить определители:
2. Даны матрицы:
Вычислить: a) b)
3. Решить матричное уравнение (найти матрицу
4. Решить системы уравнений двумя способами: по формулам Крамера и с помощью обратной матрицы. а)
5. Исследовать системы уравнений и найти решение, если оно существует. а)
б)
в)
6. Исследовать и решить системы уравнений. а)
б)
в) Приложение В приложении приведены примеры работы с матрицами и примеры решения систем с использованием математического пакета MATHEMATICA Первоначально студент должен ознакомиться с работой интерфейса. Для любой работы необходимо знать операции ввода, вывода результатов; команды для выполнения операций. Ввод данных осуществляется через знак «=». Программа подтверждает ввод строкой «In[1]:=…». Результат выполнения операции находится в строке, начинающейся словом «Out[1]=». Номера в квадратных скобках ввода и вывода совпадают. Выполнение любой операции происходит по команде со строгим выполнением заданного формата. Найти эти форматы можно в справке VIRTUAL BOOK. Там же приведены примеры выполнения операций. Ниже приведен ряд команд для выполнения заданий по теме.
Ввод матрицы. In[4]:= m1 = {{2, -5, 4}, {3, -1, 8}, {2, 6, 1}, {-1, 3, 4}} Имя матрицы m1. Сама матрица вводится построчно с использование фигурных скобок.
Умножение матриц. Команда для умножении «.».
Вычисление определителя. In[10]:= Det[m2] Матрица m2 введена выше.
Нахождение обратной матрицы.
m4 = {{2, 1}, {8, 7}, {3, -5}, {-4, 6}}
Определение ранга матрицы. In[18]:= MatrixRank[m1]
В этом примере система имеет единственное решение. Вместо знака равенства в ответе используется «->». Ниже система, имеющая множество решений и система, не имеющая решений.
Наряду со строчной записью ввода вывода использоваться записью матриц и других математических объектов в привычном виде. Для этого можно использовать команду TraditionalForm
Введение Настоящее пособие предназначено для знакомства с основами линейной алгебры и содержит разделы, посвященные теории матриц и теории систем линейных уравнений. Оно предназначено студентам 1-го курса и может быть полезно всем, кого интересует простое и компактное изучение материала. В каждом параграфе, кроме краткого изложения теории, содержатся примеры с решениями и упражнения для самостоятельного решения. Приведены также типовые индивидуальные задания. Нумерация формул и рисунков в пособии сквозная. Ключевые слова в определениях и формулировках утверждений выделены курсивом. С развитием компьютерной техники появилась возможность решать многие задачи линейной алгебры, не очень доступные в недалеком прошлом ввиду сложности вычислений. Как известно, для решения математических задач существует много различных программных пакетов. Универсальным пакетом является пакет MATHEMATICA. Примеры вычислений в пакете MATHEMATICA в приложении. Освоив предложенные в пособии методы вручную, рекомендуем проделать вычисления с использованием компьютера.
Литература.
1. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1977. 2. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. – СПб.: Издательство «Лань», 1998. 3. Краснов М.Л., Киселев А.И., Макаренко Г.И., Шикин Е.В., Заляпин В.И., Соболев С.К. Вся высшая математика: Учебник. Т. 1. – М.: Эдиториал УРСС, 2000. 4. Данко П.Е, Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.: Высшая школа, 1999. Ч.1.- 304 с. - Ч.2. - 416 с. 5. Фридман Г. Н., Леора С.Н. Математика & Mathematica. Избранные задачи для избранных студентов. – Невский Диалект, БХВ-Петербург, 2010, 299 с.
Матрицы и действия с матрицами.
Матрицей размера
либо При необходимости указать размер матрицы будем использовать запись Элементы матрицы, имеющие одинаковые индексы, называются диагональными. Матрица, у которой ниже главной диагонали стоят нули, называется треугольной. Матрица, состоящая из одной строки, называется матрицей-строкой, а матрица, состоящая из одного столбца – матрицей-столбцом. Обе такие матрицы называют также вектором. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается Если число строк матрицы равно числу столбцов, то матрица называется квадратной, а число строк (столбцов) порядком матрицы. Квадратная матрица, у которой только диагональные элементы могут быть не равны нулю, называется диагональной матрицей Диагональная матрица, у которой все диагональные элементы равны единице, называется е диничной матрицей и обозначается Матрица, полученная из исходной перестановкой строк со столбцами, называется транспонированной по отношению к исходной и обозначается Заметим, что В математике матрица рассматривается как самостоятельный математический объект, с которым можно производить различные действия. 1. Сравнение матриц. Две матрицы равны, если они имеют одинаковый размер и соответствующие элементы равны:
2. Умножение матрицы на число. Для того чтобы умножить матрицу на число надо умножить на это число все элементы матрицы:
3. Сложение (вычитание) матриц. Сложение (вычитание) матриц проводится поэлементно и возможно для матриц одного размера:
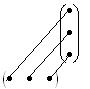
4. Умножение матриц. Матрицы перемножаются по правилу строки на столбец.
Рис.1 А именно, элементы, соединенные одной линией перемножаются, а затем результаты складываются. Для того чтобы получить элемент ►Пример 1. Даны матрицы Решение.
◄ Умножение матриц возможно только в случае, если число столбцов первой матрицы равно числу строк второй матрицы. Результат умножения – матрица, имеющая число строк, совпадающее с числом строк первой матрицы, и число столбцов равное числу столбцов второй матрицы. При умножении матрицы на вектор-столбец получаем вектор-столбец. При умножении матрицы на транспонированную матрицу получаем квадратную матрицу. Умножение матриц не коммутативно (см. пример 1). Более того, при перестановке (коммутации) матриц подчас умножение не всегда возможно. Те квадратные матрицы, для которых выполнено свойство Для матриц выполнены ассоциативный и дистрибутивный законы умножения, если не нарушаетс
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 912; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.013 с.) |

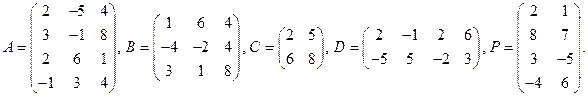
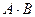 . 2)
. 2) 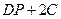 . 3)
. 3) 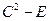 . 4)
. 4)  . 5)
. 5) 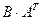 .
.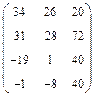 . 2)
. 2) 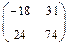 . 3)
. 3) 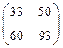 . 4)
. 4) 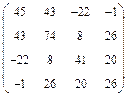 . 5)
. 5) 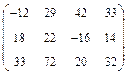 .
. , если
, если 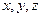 удовлетворяют условию
удовлетворяют условию 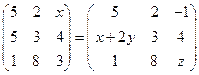 . Ответ:
. Ответ:  .
. , если
, если 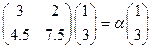 . Ответ:
. Ответ: 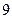 .
.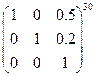 . Ответ:
. Ответ: 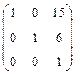 .
. , вычисляемая по определенному правилу (см., например,
, вычисляемая по определенному правилу (см., например,  ). Обозначается определитель одним из символов
). Обозначается определитель одним из символов 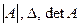 .
. , состоящей из одного числа, равен самому числу.
, состоящей из одного числа, равен самому числу.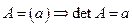 .
.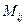 определителя
определителя  -го порядка называется определитель, полученный из данного вычеркиванием
-го порядка называется определитель, полученный из данного вычеркиванием 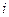 - ой строки и
- ой строки и  -го столбца.
-го столбца. В частности, сам определитель квадратной матрицы тоже является ее минором. Миноры
В частности, сам определитель квадратной матрицы тоже является ее минором. Миноры  определителя
определителя  называется выражение
называется выражение .
. )-го порядка.
)-го порядка. (1)
(1)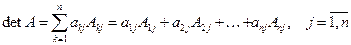 . (2)
. (2)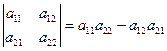 . (3)
. (3)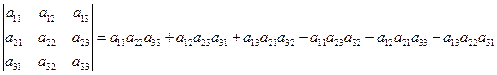 (4)
(4) .
. .
.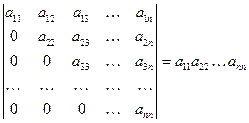 .
. .
. .
. . ◄
. ◄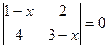 .
.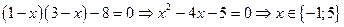 . ◄
. ◄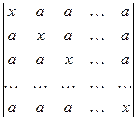 .
.
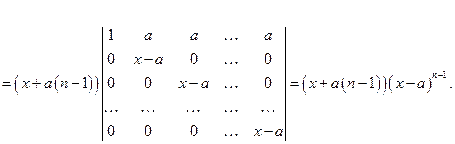 ◄
◄ ; б)
; б) 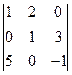 . в)
. в) 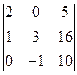 . г)
. г) 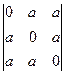 ;
; ; е)
; е)  ; ж)
; ж) 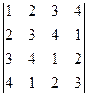 ; з)
; з) 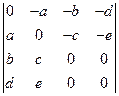 ;
; ; к)
; к) 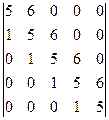 .
.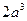 д) 0; е) 48; ж)160; з)
д) 0; е) 48; ж)160; з) 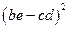 ;и)394; к) 665.
;и)394; к) 665. , при котором
, при котором 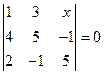 . Ответ: -3.
. Ответ: -3.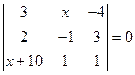 . Ответ: 2.
. Ответ: 2.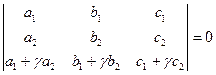 ; б)
; б) 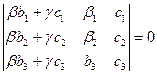 ;
;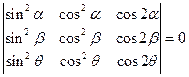 ; г)
; г) 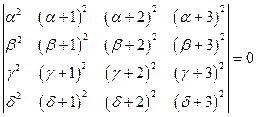 .
. .
. .
. ; б)
; б) 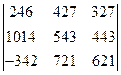 .
. ;г)
;г) 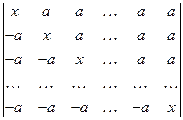 .
. ;г)
;г)  .
.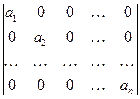 . Ответ:
. Ответ: 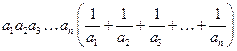 .
.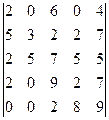 , показать, что он тоже делится на 17.
, показать, что он тоже делится на 17.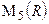 - множество вещественных матриц 5-го порядка. Существует ли такая матрица
- множество вещественных матриц 5-го порядка. Существует ли такая матрица 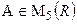 , что
, что 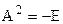 , где Е – единичная матрица? Здесь
, где Е – единичная матрица? Здесь 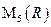 - множество всех квадратных матриц размера
- множество всех квадратных матриц размера 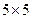 , элементами которых являются действительные числа.
, элементами которых являются действительные числа.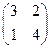 ; б)
; б)  ;в)
;в)  ;г)
;г)  ;д)
;д)  .
.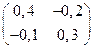 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; .
. ; б)
; б)  ;в)
;в)  ;
; ; д)
; д)  .
.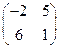 ; б)
; б)  ; д)
; д)  ) называется порядок отличного от нуля минора этой матрицы при условии, что все ее миноры высших порядков равны нулю. Минор наивысшего порядка, отличный от нуля, называется базисным минором или просто б азисом. Матрица может иметь несколько различных базисов. Для определения базиса над матрицей производят элементарные преобразования, при которых ранг матрицы не изменяется.
) называется порядок отличного от нуля минора этой матрицы при условии, что все ее миноры высших порядков равны нулю. Минор наивысшего порядка, отличный от нуля, называется базисным минором или просто б азисом. Матрица может иметь несколько различных базисов. Для определения базиса над матрицей производят элементарные преобразования, при которых ранг матрицы не изменяется. или
или  .
. .
.
 , а все миноры четвертого порядка равны нулю, т.к. содержат нулевую строку. Следовательно,
, а все миноры четвертого порядка равны нулю, т.к. содержат нулевую строку. Следовательно,  . ◄
. ◄ (множестве векторов с операциями сложения и умножения на число) имеется система из
(множестве векторов с операциями сложения и умножения на число) имеется система из  векторов
векторов
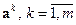 , называется выражение
, называется выражение ,
, - числа.
- числа. , то, комбинация
, то, комбинация  , называется тривиальной комбинацией. Она, очевидно, равна
, называется тривиальной комбинацией. Она, очевидно, равна  =(0,0,..,0), где
=(0,0,..,0), где  называются линейно независимыми, если любая нетривиальная комбинация этих векторов не равна нулевому вектору.
называются линейно независимыми, если любая нетривиальная комбинация этих векторов не равна нулевому вектору. называются линейно зависимыми, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору.
называются линейно зависимыми, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору. .
. .
. ; б)
; б)  ; в)
; в)  ;
; . Ответы: а) 4; б) 2; в) 4; г) 3.
. Ответы: а) 4; б) 2; в) 4; г) 3.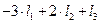 .
. (линейной системой) называется система вида
(линейной системой) называется система вида (7)
(7) - числа. Числа
- числа. Числа  называются коэффициентами системы, а числа
называются коэффициентами системы, а числа  - свободными членами.
- свободными членами. (8)
(8) , (9)
, (9) . Нулевое решение однородной системы называется тривиальным.
. Нулевое решение однородной системы называется тривиальным. – матрица коэффициентов при неизвестных,
– матрица коэффициентов при неизвестных, - матрица-столбец свободных членов,
- матрица-столбец свободных членов, - матрица-столбец неизвестных.
- матрица-столбец неизвестных. ,
, .
.

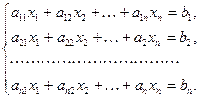 (10)
(10)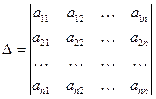 ,
, , где
, где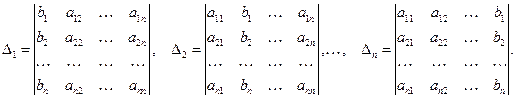
 , получены из главного определителя заменой соответствующего столбца на столбец свободных членов.
, получены из главного определителя заменой соответствующего столбца на столбец свободных членов.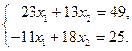
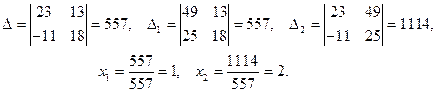
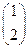 .◄
.◄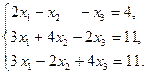 2)
2) 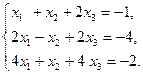 3)
3) 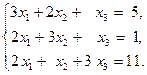
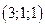 , 2)
, 2) 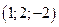 , 3)
, 3) 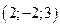 .
.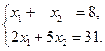 б)
б)  в)
в) 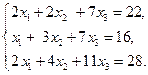
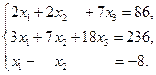 Ответы: а)
Ответы: а) 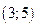 ; б)
; б) 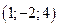 ; в)
; в)  4 г)
4 г) 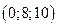 .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  .
. Ответ:
Ответ:  линейно независимых строк, а затем вычислить миноры, поочередно вычеркивая столбцы и изменяя знак при каждом переходе.
линейно независимых строк, а затем вычислить миноры, поочередно вычеркивая столбцы и изменяя знак при каждом переходе.
 , где
, где  принимает любое значение.
принимает любое значение.
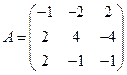 . Определитель
. Определитель  Минор
Минор  Следовательно, ранг матрицы коэффициентов равен двум и на единицу меньше числа неизвестных. Оставив две линейно независимых строки в матрице
Следовательно, ранг матрицы коэффициентов равен двум и на единицу меньше числа неизвестных. Оставив две линейно независимых строки в матрице  , получаем
, получаем .
. . ◄
. ◄ 2)
2) 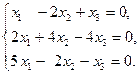 3)
3) 
 ; 2)
; 2)  ; 3)
; 3)  ;
;  .
.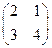 , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  , 6)
, 6) 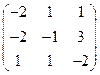 , 7)
, 7) 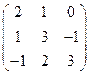 .
. ;
; ;
; ;
; ;
; ;
; ;
; .
. ,
,  ,
,  .
. ,
, 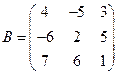 ,
,  ,
,  .
. , где
, где  - единичная матрица.
- единичная матрица. (вычисления проводить, сохраняя три знака после запятой).
(вычисления проводить, сохраняя три знака после запятой). ).
). .
. б)
б) 




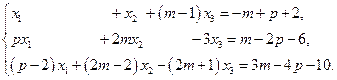

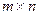 называется прямоугольная таблица чисел, содержащая
называется прямоугольная таблица чисел, содержащая 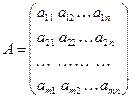 .
.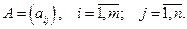
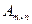 .
. .
. :
:  .
.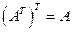 .
. .
. .
. . Для перечисленных выше действий справедливы следующие свойства:
. Для перечисленных выше действий справедливы следующие свойства: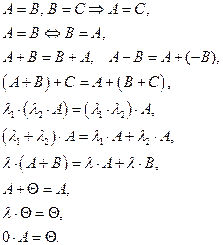
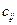 матрицы
матрицы 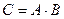 надо каждый элемент
надо каждый элемент  . Найти
. Найти  .
.
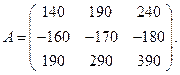
 .
.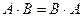 , называются коммутативными.
, называются коммутативными.


