Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы. Определители. СистемыСодержание книги Поиск на нашем сайте
МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Свойства действий с матрицами
1. А + В = В + А 2. (А + В) + С = А + (В + С) 3. λ (А + В) = λА + λВ 4. А · (В + С) = А · В + А · С 5. λ · (АВ) = (λА) · В = А · (λВ) 6. А · (ВС) = (АВ) · С 7. (АТ)Т = А 8. (λА)Т = λ · АТ 9. (А+В)Т = АТ + ВТ 10. (АВ)Т = ВТ · АТ Примеры для самостоятельной работы Выполнить действия над матрицами: 1. 3. 5.
Обратная матрица
Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля, т.е. detA ≠ 0. Матрица А–1 называется обратной квадратной матрице А, если при умножении этой матрицы на данную как слева, так и справа получается единичная матрица:
Теорема. Для невырожденной матрицы существует обратная матрица.
Обратная матрица вычисляется по формуле:
Пример. Найти обратную матрицу для матрицы
Вычислим определитель данной матрицы
значит, А–1 существует. Вычисляем алгебраические дополнения Аij элементов матрицы:
Запишем А–1, в которой второй сомножитель получен транспонированием матрицы из алгебраических дополнений:
Правильность вычисления обратной матрицы можно проверить по формулам
Примеры для самостоятельной работы
Найти обратную матрицу 1.
3.
Ранг матрицы
Наивысший порядок минора, отличного от нуля, называется рангом матрицы. Обозначается rang A или r(A), r(Am×n) ≤ min{m, n}. При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка Δk, отличный от нуля, то требуется вычислить лишь миноры (k+1)-го порядка, окаймляющие минор Δk. Если все они равны нулю, то ранг матрицы равен k. Пример. Найти ранг матрицы:
Возьмем отличный от нуля минор 2-го порядка
Минор 3-го порядка
окаймляющий минор Δ2, отличен от нуля. Два минора 4-го порядка, окаймляющие минор Δ3, равны нулю:
Таким образом, ранг матрицы А равен трем (rangA = 3). Для облегчения вычисления ранга матрицы используются элементарные преобразования матрицы, сохраняющие ранг матрицы: 1) отбрасывание нулевой строки (столбца); 2) умножение всех элементов строки (столбца) матрицы на число, не равное нулю;
3) изменение порядка строк (столбцов) матрицы; 4) прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число; 5) транспонирование матрицы. Матрица, полученная из данной элементарными преобразованиями, называется эквивалентной данной, обозначается знаком ~.
Примеры для самостоятельной работы
Найти ранг матрицы: 1.
Системы линейных уравнений
Система уравнений вида:
где aij – коэффициенты; xj – переменные; bi – свободные члены, называется системой линейных уравнений. Решить систему линейных уравнений – значит указать такие наборы значений переменных, которые обращают уравнения системы в тождества. Система линейных уравнений называется: а) совместной, если она имеет хотя бы одно решение; б) несовместной, если она не имеет решений; в) определенной, если она имеет единственное решение; г) неопределенной, если она имеет более одного решения; д) однородной, если все bi = 0; е) неоднородной, если есть bi ≠ 0. Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Правило Крамера
Правило Крамера применяется к системам, у которых число уравнений m равно числу переменных n. Рассмотрим систему двух линейных уравнений с двумя переменными:
Вычислим определители
1. Если Δ ≠ 0, то система имеет единственное решение, определяемое по формулам Крамера
2. Если Δ = 0, а хотя бы один из определителей Δх или Δy отличен от нуля, то система не имеет решений. 3. Если Δ= Δх = Δy = 0, то система имеет бесконечно много решений. Пример. Решить систему по правилу Крамера:
Вычислим определители:
Рассмотрим систему трех уравнений с тремя неизвестными:
Вычислим определители
1. Если ∆ ≠ 0, то система имеет единственное решение
2. Если ∆ = 0, а хотя бы один из определителей ∆x, ∆y, ∆z отличен от нуля, то система не имеет решений. 3. Если ∆ = ∆x = ∆y = ∆z = 0, то возможны случаи: а) система не имеет решений; б) система имеет бесконечно много решений. Пример. Решить систему по правилу Крамера:
Вычислим определители:
По формулам Крамера
Пример. Решить систему по правилу Крамера:
Вычислим определители:
Система не имеет решений.
Метод Гаусса
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Элементарные преобразования системы уравнений состоят в выполнении следующих действий: 1) перестановка местами двух уравнений; 2) умножение обеих частей какого-либо уравнения на число λ ≠ 0; 3) прибавление к одному уравнению системы другого уравнения, умноженного на число. Пример. Решить систему уравнений методом Гаусса:
Исключим переменную x из 2-го и 3-го уравнений системы. Умножим первое уравнение на (-2) и прибавим ко 2-му уравнению, затем умножим 1-е уравнение на (-1) и прибавим к 3-му уравнению системы. Получим систему уравнений
Разделим 2-е уравнение на (-3) и получим систему уравнений
Исключим переменную y из 3-го уравнения системы, для этого умножим 2-е уравнение на 2 и прибавим к 3-му уравнению, получим систему уравнений
Выразим переменную z из 3-го уравнения, y – из 2-го уравнения, переменную х из 1-го уравнения
Имеем x=1, y=2, z=3 – единственное решение системы. Пример. Решить систему уравнений методом Гаусса:
Умножим 1-е уравнение на (-2) и прибавим ко 2-му уравнению, затем прибавим 1-е уравнение к 3-му уравнению. Получим систему уравнений:
Далее умножим 2-е уравнение на 2 и прибавим к 3-му уравнению:
В полученной системе имеем противоречие 0 = 6, значит, исходная система несовместна. Пример. Решить систему уравнений методом Гаусса
Исключим переменную x 1 из 2-го, 3-го и 4-го уравнений системы. Умножим 1-е уравнение на (-2) и прибавим ко 2-му и 3-му уравнениям, умножим 1-е уравнение на (-3) и прибавим к 4-му уравнению. Получим систему уравнений
Исключим переменную x 2 из 3-го и 4-го уравнений системы. Умножим 2-е уравнение на
Исключим переменную х 3 из 4-го уравнения системы. Для этого умножим 3-е уравнение на (-1) и прибавим к 4-му уравнению системы. После удаления последнего уравнения система уравнений примет вид
Из этой системы обратным ходом метода Гаусса находим
Так как х 4 может принимать любые значения, то система имеет бесконечное множество решений.
Примеры для самостоятельной работы
Решить следующие системы линейных уравнений: 1. 3.
5.
Теорема Кронекера-Капелли
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы. Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.
ВЕКТОРЫ НА ПЛОСКОСТИ
Своими координатами Пусть даны векторы
или При умножении вектора на число все его координаты умножаются на это число
Два вектора
aх = bx; ay = by; az = bz .
Необходимым и достаточным условием коллинеарности векторов
Если известны координаты начала А(х1, у1, z1) и конца В(х2, у2, z2) вектора Длину вектора, заданного координатами начала и конца, вычисляют по формуле
Пример. Даны векторы
= (2 - 9; -6 -12; 4 -(-15)) = (-7; -18; 19);
= (3; -9; 6) + (12; 16; -20)=(3 + 12; -9 + 16; 6 + (-20)) = (15; 7; -14). Пример. Даны две точки А(9; -7; -4) и В(-1; 3; 1). Найти координаты и длину вектора
Пример. Дан вектор Разложение вектора Длина вектора Орт вектора Пример. Определить, при каких a и b векторы Запишем условие коллинеарности векторов: Пример. Найти длину и направляющие косинусы вектора Найдем координаты вектора Модуль вектора
Его свойства Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла между ними. Обозначается
Свойства скалярного произведения: 1) 2) 3) 4) скалярное произведение равно нулю тогда и только тогда, когда векторы 5) скалярный квадрат вектора равен квадрату его длины: Пусть даны два вектора Скалярное произведение двух векторов равно сумме произведений их одноименных координат
Условие перпендикулярности двух ненулевых векторов
Косинус угла между двумя векторами определяется по формуле:
Проекция вектора
Пример. Найти длину вектора По свойству 5:
= = 81 + 72 + 64 = 217, Пример. Найти косинус угла между векторами
= Пример. При каком значении l векторы Условие перпендикулярности записывается: Пример. Даны векторы Имеем
Примеры для самостоятельной работы 1. Найти длины диагоналей параллелограмма, построенного на векторах
2. Найти угол между единичными векторами 3. Даны вершины треугольника А(4; 1; 0); В(2; 2; 1) и С(6; 3; 1). Найти проекцию стороны АВ на АС, угол между сторонами АВ и АС. 4. При каком a векторы 5. Известно, что 6. Даны векторы ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Если известны точка М0(х0, у0) на прямой l и направляющий вектор
Если известны точка М0(х0, у0) на прямой l и вектор А(х -х0) + В(у -у0) = 0. Вектор Ах + Ву + С = 0. Если С = 0, то прямая проходит через начало координат, ее уравнение Ах + Ву = 0. Если А = 0, то прямая параллельна оси Ох, ее уравнение Если В = 0, то прямая параллельна оси Оу и Если А = С = 0, то у = 0 – ось Ох. Если В = С = 0, то х = 0 – ось Оу. Пусть даны уравнения двух прямых 1) совпадают, если 2) параллельны, если 3) перпендикулярны, если A1А2 + B1В2 = 0. Для нахождения точки пересечения прямых решают систему уравнений
Уравнение вида у = kx + b называется уравнением прямой с угловым коэффициентом, где k = tga - тангенс угла наклона прямой, b – координата точки пересечения прямой с осью Oу. Если даны уравнения двух прямых у = k1x + b1; у = k2x + b2, то а) угол между прямыми определяется по формуле
б) если k1 = k2, то прямые параллельны; в) если Уравнение прямой, проходящей через данную точку М0(х0, у0) с угловым коэффициентом k имеет вид:
Уравнение прямой, проходящей через две данные точки М1(х1, у1) и М2(х2, у2):
Расстояние от точки М0(х0, у0) до прямой Ах + Ву + С = 0 вычисляется по формуле
Пусть даны точки А(х1, у1) и В(х2, у2). Координаты точки М, делящей отрезок АВ в заданном отношении
Пример. Даны точка М(3; 4) на прямой l и направляющий вектор Уравнение имеет вид Пример. Даны точки М1(4; -2) и М2 (3; 1). Написать уравнение прямой, проходящей через точки М1 и М2. Уравнение прямой записывается Пример. Написать уравнение прямой, проходящей через точку А (1; -2) параллельно прямой 3х + 4у – 5 = 0. Найдем угловой коэффициент данной прямой, выразим
Искомая прямая имеет уравнение Подставим координаты точки А в это уравнение:
Пример. Определить взаимное расположение прямых х + 2у -3 = 0 и 5х + 10у - 2 = 0. Имеем Пример. Найти расстояние от точки М(-1; 1) до прямой 4х - 3у + 6 = 0. Искомое расстояние находится по формуле
Примеры для самостоятельной работы 1. Найти проекцию точки А(-1; 2) на прямую 3х - 5у - 21 = 0. 2. Даны вершины параллелограмма А(9; -3), В(4; -2) и С(-7; -5). Найти уравнения диагоналей. 3. Дан треугольник с вершинами А(5; -4), В(-1; 3) и С(-3; -2). Найти:
а) уравнение высоты ВD; б) уравнение меридианы ВМ; в) угол между высотой и медианой ВМ. 4. Доказать, что три точки А(3; -5), В(-1; 1) и С(-3; 4) лежат на одной прямой. 5. Стороны треугольника заданы уравнениями: 7х - 6у + 9 = 0; 5х + 2у - 25 = 0; 3х + 10у + 29 = 0. Найти координаты вершин и уравнения высот треугольника. КРИВЫЕ ВТОРОГО ПОРЯДКА Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем виде уравнение имеет вид: Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0. 1. Окружность – множество точек плоскости, равноудаленных от данной. Каноническое уравнение окружности (х - х0)2 + (у - у0)2 = R2, где точка С(х0, у0) – центр окружности, R – ее радиус. Пример. Определить вид кривой х2 + у2 - 6х + 4у – 12 = 0. Выделим полный квадрат для каждой переменной х и у: х2 - 6х + 9 – 9 + у2 + 4у + 4 – 4 – 12 = 0, (х - 3)2 + (у + 2)2 = 25 – это уравнение окружности с центром в точке С(3; -2) и R = 5. 2. Эллипсом называется множество всех точек плоскости, сумма расстояний которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная (2а). F1M + F2M = 2a. Каноническое уравнение эллипса имеет вид: (b2 = a2 - c2, a > c), F1(-с; 0) и F2 (с; 0) – фокусы.
Точки А1 (-а, 0), А2 (а, 0), В1 (0, -b), В2 (0, b) называются вершинами эллипса, отрезки ОА2 = а, ОВ2 = b – большая и малая полуоси. Величина Пример. Найти каноническое уравнение эллипса, зная его большую полуось а = 12 и эксцентриситет e = 0,5. По определению
3. Гиперболой называется множество всех точек плоскости, абсолютное значение разности расстояний которых до двух данных точек F1 и F2 (фокусов) есть величина постоянная (2а). |F1М - F2М| = 2а. Каноническое уравнение гиперболы F1(-с, 0), F2(с, 0) – фокусы.
Отрезки ОА2 = а – действительная полуось, ОВ2 = b – мнимая полуось гиперболы.
Пример. Найти каноническое уравнение гиперболы, зная уравнения асимптот Зная F1F2 = 2с = 20, находим с = 10. Из уравнений асимптот
4. Параболой называется множество точек плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой, FM = NM.
Каноническое уравнение параболы, симметричной оси Ох, у2 = 2рх (р > 0).
Уравнение параболы, симметричной оси Оу, имеет вид: х2 = 2ру, Пример. Найти уравнение параболы, проходящей через точку А(2, 4) и симметричной оси Ох. В каноническое уравнение у2 = 2рх подставим координаты точки А: 16 = 4р, р = 4. Уравнение параболы примет вид у2 = 8х. Примеры для самостоятельной работы 1. Составить каноническое уравнение эллипса, зная его малую полуось b = 2 2. Найти координаты фокусов, полуоси и эксцентриситет гиперболы 9х2 - 16у2 = 144. 3. Найти каноническое уравнение гиперболы, проходящей через точки А (2; 1) и В(- 4; 4. Определить вид кривой у2 - 2х + 4у + 2 = 0. 5. Найти фокус и уравнение директрисы параболы у2 = 24х. ВВЕДЕНИЕ В АНАЛИЗ
Если каждому элементу x Множество Х называется областью определения функции, а множество Y – областью её значений. Существуют следующие способы задания функции: табличный, графический, аналитический, словесный. Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные). К алгебраическим относятся: целая рациональная, дробно-рациональная и иррациональная функции.
Теоремы о пределах
Если существуют пределы 1. Предел постоянной равен этой постоянной:
2. Предел суммы конечного числа функций равен сумме пределов этих функций:
3. Предел произведения конечного числа функций равен произведению пределов этих функций:
Постоянный множитель можно выносить за знак предела:
4. Предел частного двух функций равен частному пределов этих функций при условии, что
Непрерывность функции
Функция f(х) называется непрерывной в точке х0 , если: 1) она определена в этой точке и в ее окрестности; 2) имеет конечный предел при 3) этот предел равен значению функции в точке х0 , то есть
Для непрерывной функции возможна перестановка символов предела и функции Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке х0, а сама точка х0 называется точкой разрыва функции. Если существуют односторонние пределы, но не равны между собой, Если хотя бы один из односторонних пределов не существует (¥), то х0 – точка разрыва второго рода. Сумма, произведение, частное непрерывных функций есть непрерывная функция. Пример. Исследовать на непрерывность функцию Функция задана различными аналитическими выражениями на интервалах (-¥, 0) и [ 0, ¥). Исследуем точку х = 0, найдем односторонние пределы:
Односторонние пределы существуют, но не равны, поэтому х = 0 – точка разрыва первого рода. Примеры для самостоятельной работы 1. Вычислить: а) в) д)
2. Исследовать на непрерывность функции: а)
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ Производная функции
Производной функц |
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.28 (0.015 с.) |

 . 2.
. 2.  .
. . 4.
. 4.  .
.

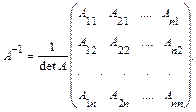
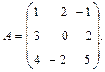




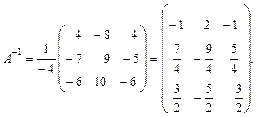
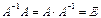 .
.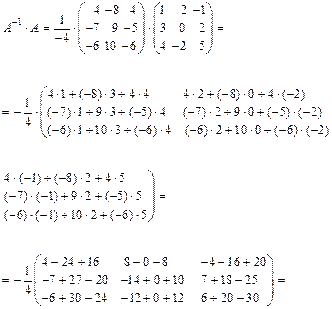

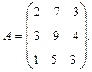 2.
2. 
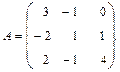



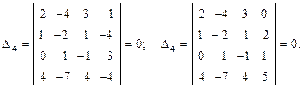
 3.
3. 
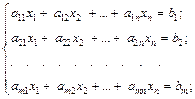


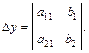
 .
.
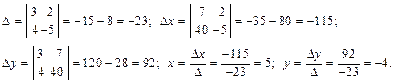



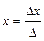 ,
, 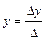 ,
, 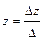 .
.





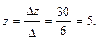

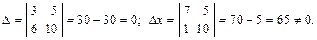
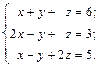
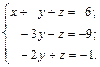


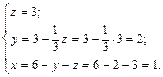
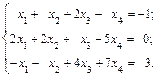

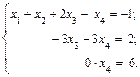

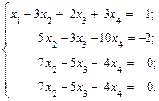
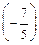 и прибавим к 3-му и 4-му уравнениям. Получим систему уравнений
и прибавим к 3-му и 4-му уравнениям. Получим систему уравнений


 2.
2. 
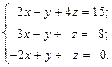 4.
4. 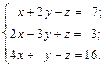
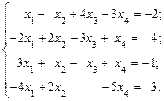 6.
6. 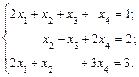
 и
и  . При сложении векторов их одноименные координаты складываются
. При сложении векторов их одноименные координаты складываются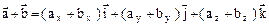
 .
. или
или  .
. и
и  равны тогда и только тогда, когда выполняются равенства
равны тогда и только тогда, когда выполняются равенства .
. , то его координаты определяются
, то его координаты определяются  .
. ;
; 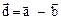 ,
,  ,
,  .
. = (1 + 3; -3 + 4; 2 + (-5)) = (4; 1; -3);
= (1 + 3; -3 + 4; 2 + (-5)) = (4; 1; -3); = (1 -3; -3 -4; 2 - (-5)) = (-2; -7; 7);
= (1 -3; -3 -4; 2 - (-5)) = (-2; -7; 7);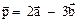 = 2 (1; - 3; 2) -3(3; 4; -5) = (2; -6; 4) - (9; 12; -15) =
= 2 (1; - 3; 2) -3(3; 4; -5) = (2; -6; 4) - (9; 12; -15) =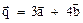 = 3 (1; -3; 2) + 4 (3; 4; -5) =
= 3 (1; -3; 2) + 4 (3; 4; -5) = .
. = (х2 -х1, у2 -у1, z2 -z1) = (-1 -9; 3-(-7); 1 -(-4)) = (-10; 10; 5);
= (х2 -х1, у2 -у1, z2 -z1) = (-1 -9; 3-(-7); 1 -(-4)) = (-10; 10; 5); =
= 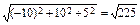 = 15.
= 15. .
. .
. .
. и
и  коллинеарны.
коллинеарны. , откуда 3a = -12; a = -4; 2b = 3, b = 3/2.
, откуда 3a = -12; a = -4; 2b = 3, b = 3/2. ;
;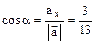 ;
;  ;
;  .
. :
: или
или  .
. - переместительный закон;
- переместительный закон; - распределительный закон;
- распределительный закон; - сочетательный закон;
- сочетательный закон; .
.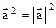 .
. и
и  . По свойствам 4 и 5 имеем
. По свойствам 4 и 5 имеем  ;
;  .
. .
. .
. .
.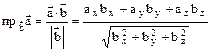 .
. , если
, если  ,
,  , угол a между векторами
, угол a между векторами  =
= = 9×9 + 12×3×4×cos60° + 4×16 =
= 9×9 + 12×3×4×cos60° + 4×16 = .
.
 .
. и
и  взаимно перпендикулярны?
взаимно перпендикулярны?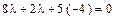 или 10l -20 = 0, l = 2.
или 10l -20 = 0, l = 2. ,
, 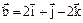 ,
,  . Найти
. Найти  ,
,  ,
,  .
. = (1; -2; 2);
= (1; -2; 2);  (10; 4; 2). Применим формулу
(10; 4; 2). Применим формулу  ,
,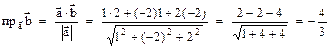 .
.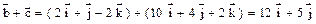 .
. .
.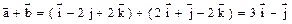 .
. .
. (3; -5; 8) и
(3; -5; 8) и  и
и  , если векторы
, если векторы  и
и  перпендикулярны.
перпендикулярны. и
и  взаимно перпендикулярны?
взаимно перпендикулярны? ,
,  . Найти скалярное произведение векторов
. Найти скалярное произведение векторов  = (7; -2; 6). Найти вектор
= (7; -2; 6). Найти вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям: 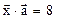 ,
,  ,
, 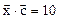 .
. = (m, n), параллельный этой прямой, то можно записать каноническое уравнение прямой
= (m, n), параллельный этой прямой, то можно записать каноническое уравнение прямой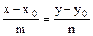 .
. = (А, В), перпендикулярный к ней, то можно записать уравнение
= (А, В), перпендикулярный к ней, то можно записать уравнение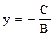 .
. .
. и
и 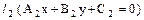 . Тогда прямые
. Тогда прямые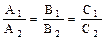 ;
;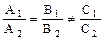 ;
;
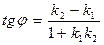 ;
; , то прямые перпендикулярны.
, то прямые перпендикулярны. .
. .
. .
.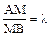 вычисляются по формулам
вычисляются по формулам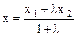 ,
, 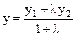 .
. .
.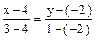 или
или 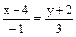 , 3х - 12 = -у - 2, 3х + у - 10 = 0.
, 3х - 12 = -у - 2, 3х + у - 10 = 0. ,
,  .
.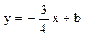 .
. ,
, и
и 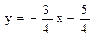 .
. . Прямые параллельны.
. Прямые параллельны.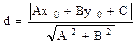 .
. .
. ,
,
 называется эксцентриситетом и характеризует вытянутость эллипса.
называется эксцентриситетом и характеризует вытянутость эллипса. , с = 6. Из соотношения b2 = а2 - с2 определим b2 = 144 - 36 = 108, тогда уравнение эллипса примет вид
, с = 6. Из соотношения b2 = а2 - с2 определим b2 = 144 - 36 = 108, тогда уравнение эллипса примет вид .
. , (b2 = c2 - a2),
, (b2 = c2 - a2),
 - асимптоты гиперболы,
- асимптоты гиперболы,  - эксцентриситет.
- эксцентриситет. и расстояние F1F2 = 20.
и расстояние F1F2 = 20. . Составим систему уравнений:
. Составим систему уравнений: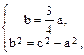
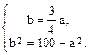
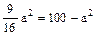 ,
,  , а2 = 64, b2 = 100 – 64 = 36. Уравнение гиперболы примет вид
, а2 = 64, b2 = 100 – 64 = 36. Уравнение гиперболы примет вид  .
.
 - фокус,
- фокус,  - директриса, р – расстояние от фокуса до директрисы.
- директриса, р – расстояние от фокуса до директрисы.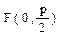 - фокус,
- фокус,  - директриса.
- директриса. и F1 F2 = 8.
и F1 F2 = 8. ).
). X ставится в соответствие определенный элемент y
X ставится в соответствие определенный элемент y 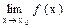 = А и
= А и  = В, то имеют место теоремы:
= В, то имеют место теоремы: = С.
= С. =
= 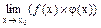 =
=  .
. ≠0:
≠0: =
=  .
. ;
; f (x) = f (x0 ).
f (x) = f (x0 ).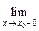 f(x) ≠
f(x) ≠ 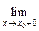 f (x), то х0 – точка разрыва первого рода.
f (x), то х0 – точка разрыва первого рода.
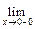 f (x) =
f (x) =  = -2,
= -2, f (x) =
f (x) =  = 0.
= 0.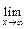
 ; б)
; б)  ;
;
 ; г)
; г) 
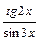 ;
; ; е)
; е)  ; ж)
; ж) 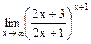 .
.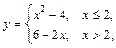 б)
б)  .
.