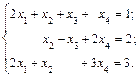Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители. Свойства определителейСодержание книги Поиск на нашем сайте
Каждой квадратной матрице можно поставить в соответствие число, называемое определителем или детерминантом. Для матрицы Пример. Вычислить Для матрицы третьего порядка
определитель третьего порядка вычисляется
Пример.
Определитель треугольной матрицы равен произведению элементов главной диагонали. Минором Mij элемента aij определителя n-го порядка называется определитель (n-1)-го порядка, полученный из данного определителя вычеркиванием i-й строки и j-го столбца. Например,
Алгебраическим дополнением Aij элемента aij определителя n-го порядка называется его минор, взятый со знаком (-1)i+j:
Пример.
Минор М31 элемента а31 получается из ∆3 вычеркиванием третьей строки и первого столбца, т.е.
Теорема. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
∆n = ai1Ai1 + ai2Ai2 + … + ainAin, где 1 ≤ i ≤ n. Пример. Вычислить определитель матрицы
Для разложения определителя выбирают тот столбец или ту строку, где есть нулевые элементы, т.к. соответствующие им слагаемые в разложении будут равны нулю.
Свойства определителей
1. Определитель транспонированной матрицы равен определителю исходной матрицы, т.е. detАТ = detA. 2. Если поменять местами две строки (два столбца) определителя, то он изменит знак. 3. Определитель с двумя одинаковыми строками (столбцами) равен нулю. 4. Если определитель содержит нулевую строку (столбец), то он равен нулю. 5. Общий множитель в строке (столбце) можно выносить за знак определителя. 6. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число. 7. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Пример. Вычислить определитель
Преобразуем определитель так, чтобы в 3-ем столбце все элементы, кроме одного, обращались в 0. Для этого элементы 1-й строки прибавим к соответствующим элементам 2-й строки; умножим элементы 1-й строки на (-2) и на (-1) и прибавим их соответственно к элементам 3-й и 4-й строк. Раскладывая полученный определитель по элементам 3-го столбца, найдем:
В полученном определителе элементы 2-го столбца умножим на 2 и прибавим их к соответствующим элементам 1-го столбца:
Примеры для самостоятельной работы Вычислите определители: 1.
3.
Обратная матрица
Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля, т.е. detA ≠ 0. Матрица А–1 называется обратной квадратной матрице А, если при умножении этой матрицы на данную как слева, так и справа получается единичная матрица:
Теорема. Для невырожденной матрицы существует обратная матрица.
Обратная матрица вычисляется по формуле:
Пример. Найти обратную матрицу для матрицы
Вычислим определитель данной матрицы
значит, А–1 существует. Вычисляем алгебраические дополнения Аij элементов матрицы:
Запишем А–1, в которой второй сомножитель получен транспонированием матрицы из алгебраических дополнений:
Правильность вычисления обратной матрицы можно проверить по формулам
Примеры для самостоятельной работы
Найти обратную матрицу 1.
3.
Ранг матрицы
Наивысший порядок минора, отличного от нуля, называется рангом матрицы. Обозначается rang A или r(A), r(Am×n) ≤ min{m, n}. При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка Δk, отличный от нуля, то требуется вычислить лишь миноры (k+1)-го порядка, окаймляющие минор Δk. Если все они равны нулю, то ранг матрицы равен k. Пример. Найти ранг матрицы:
Возьмем отличный от нуля минор 2-го порядка
Минор 3-го порядка
окаймляющий минор Δ2, отличен от нуля. Два минора 4-го порядка, окаймляющие минор Δ3, равны нулю:
Таким образом, ранг матрицы А равен трем (rangA = 3). Для облегчения вычисления ранга матрицы используются элементарные преобразования матрицы, сохраняющие ранг матрицы: 1) отбрасывание нулевой строки (столбца); 2) умножение всех элементов строки (столбца) матрицы на число, не равное нулю; 3) изменение порядка строк (столбцов) матрицы;
4) прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число; 5) транспонирование матрицы. Матрица, полученная из данной элементарными преобразованиями, называется эквивалентной данной, обозначается знаком ~.
Примеры для самостоятельной работы
Найти ранг матрицы: 1.
Системы линейных уравнений
Система уравнений вида:
где aij – коэффициенты; xj – переменные; bi – свободные члены, называется системой линейных уравнений. Решить систему линейных уравнений – значит указать такие наборы значений переменных, которые обращают уравнения системы в тождества. Система линейных уравнений называется: а) совместной, если она имеет хотя бы одно решение; б) несовместной, если она не имеет решений; в) определенной, если она имеет единственное решение; г) неопределенной, если она имеет более одного решения; д) однородной, если все bi = 0; е) неоднородной, если есть bi ≠ 0. Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Правило Крамера
Правило Крамера применяется к системам, у которых число уравнений m равно числу переменных n. Рассмотрим систему двух линейных уравнений с двумя переменными:
Вычислим определители
1. Если Δ ≠ 0, то система имеет единственное решение, определяемое по формулам Крамера
2. Если Δ = 0, а хотя бы один из определителей Δх или Δy отличен от нуля, то система не имеет решений. 3. Если Δ= Δх = Δy = 0, то система имеет бесконечно много решений. Пример. Решить систему по правилу Крамера:
Вычислим определители:
Рассмотрим систему трех уравнений с тремя неизвестными:
Вычислим определители
1. Если ∆ ≠ 0, то система имеет единственное решение
2. Если ∆ = 0, а хотя бы один из определителей ∆x, ∆y, ∆z отличен от нуля, то система не имеет решений. 3. Если ∆ = ∆x = ∆y = ∆z = 0, то возможны случаи: а) система не имеет решений; б) система имеет бесконечно много решений. Пример. Решить систему по правилу Крамера:
Вычислим определители:
По формулам Крамера
Пример. Решить систему по правилу Крамера:
Вычислим определители:
Система не имеет решений.
Метод Гаусса
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Элементарные преобразования системы уравнений состоят в выполнении следующих действий: 1) перестановка местами двух уравнений; 2) умножение обеих частей какого-либо уравнения на число λ ≠ 0; 3) прибавление к одному уравнению системы другого уравнения, умноженного на число. Пример. Решить систему уравнений методом Гаусса:
Исключим переменную x из 2-го и 3-го уравнений системы. Умножим первое уравнение на (-2) и прибавим ко 2-му уравнению, затем умножим 1-е уравнение на (-1) и прибавим к 3-му уравнению системы. Получим систему уравнений
Разделим 2-е уравнение на (-3) и получим систему уравнений
Исключим переменную y из 3-го уравнения системы, для этого умножим 2-е уравнение на 2 и прибавим к 3-му уравнению, получим систему уравнений
Выразим переменную z из 3-го уравнения, y – из 2-го уравнения, переменную х из 1-го уравнения
Имеем x=1, y=2, z=3 – единственное решение системы. Пример. Решить систему уравнений методом Гаусса:
Умножим 1-е уравнение на (-2) и прибавим ко 2-му уравнению, затем прибавим 1-е уравнение к 3-му уравнению. Получим систему уравнений:
Далее умножим 2-е уравнение на 2 и прибавим к 3-му уравнению:
В полученной системе имеем противоречие 0 = 6, значит, исходная система несовместна. Пример. Решить систему уравнений методом Гаусса
Исключим переменную x 1 из 2-го, 3-го и 4-го уравнений системы. Умножим 1-е уравнение на (-2) и прибавим ко 2-му и 3-му уравнениям, умножим 1-е уравнение на (-3) и прибавим к 4-му уравнению. Получим систему уравнений
Исключим переменную x 2 из 3-го и 4-го уравнений системы. Умножим 2-е уравнение на
Исключим переменную х 3 из 4-го уравнения системы. Для этого умножим 3-е уравнение на (-1) и прибавим к 4-му уравнению системы. После удаления последнего уравнения система уравнений примет вид
Из этой системы обратным ходом метода Гаусса находим
Так как х 4 может принимать любые значения, то система имеет бесконечное множество решений.
Примеры для самостоятельной работы
Решить следующие системы линейных уравнений: 1. 3.
5.
Теорема Кронекера-Капелли
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы. Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.
ВЕКТОРЫ НА ПЛОСКОСТИ
|
|||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.11.69 (0.011 с.) |

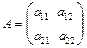 определитель второго порядка запишется
определитель второго порядка запишется 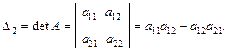
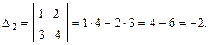
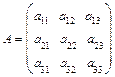
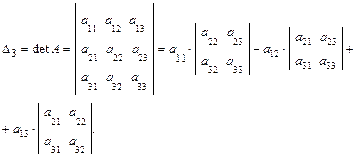
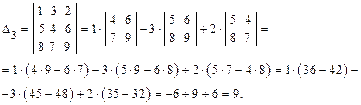
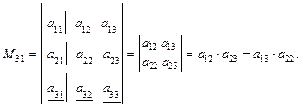
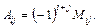
 Минор М23 элемента а23 получается из ∆3 вычеркиванием второй строки и третьего столбца, т.е.
Минор М23 элемента а23 получается из ∆3 вычеркиванием второй строки и третьего столбца, т.е. 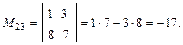
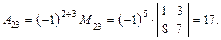
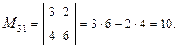
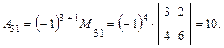
 .
.
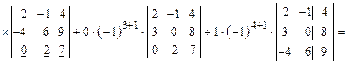
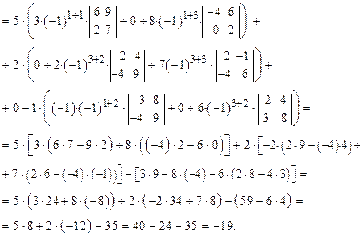
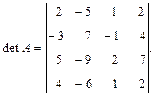



 2.
2. 
 4.
4. 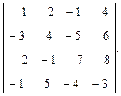

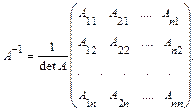
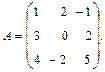


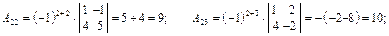

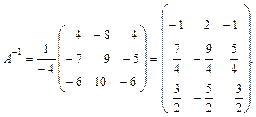
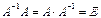 .
.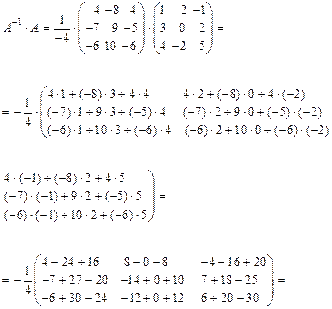

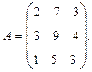 2.
2. 
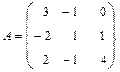



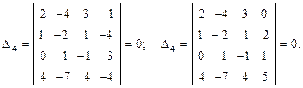
 3.
3. 
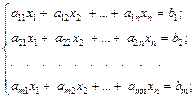


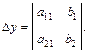
 .
.
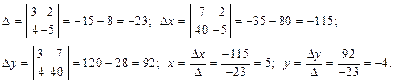



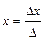 ,
, 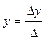 ,
, 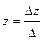 .
.





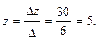

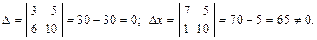
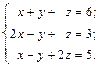
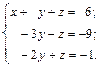


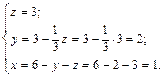
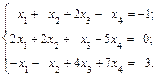

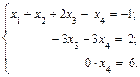

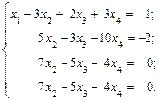
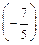 и прибавим к 3-му и 4-му уравнениям. Получим систему уравнений
и прибавим к 3-му и 4-му уравнениям. Получим систему уравнений


 2.
2. 
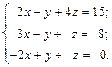 4.
4. 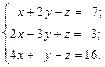
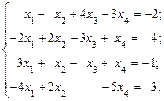 6.
6.