
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раскрытие неопределенностей. Замечательные пределыСодержание книги Поиск на нашем сайте
К неопределенностям относятся выражения вида: Пример. Найти: 1) Имеем неопределенности вида 1) = 2) = 3) = так как знаменатель дроби Пример. Подставим предельное значение х = 2, получим неопределенность
Пример. Имеем неопределенность вида (
Первым замечательным пределом называется Вторым замечательным пределом называется:
Пример. При х®0 имеем неопределенность
Пример. Имеем неопределенность 1¥. Воспользуемся вторым замечательным пределом.
Непрерывность функции
Функция f(х) называется непрерывной в точке х0 , если: 1) она определена в этой точке и в ее окрестности; 2) имеет конечный предел при 3) этот предел равен значению функции в точке х0 , то есть
Для непрерывной функции возможна перестановка символов предела и функции Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке х0, а сама точка х0 называется точкой разрыва функции. Если существуют односторонние пределы, но не равны между собой, Если хотя бы один из односторонних пределов не существует (¥), то х0 – точка разрыва второго рода. Сумма, произведение, частное непрерывных функций есть непрерывная функция. Пример. Исследовать на непрерывность функцию Функция задана различными аналитическими выражениями на интервалах (-¥, 0) и [ 0, ¥). Исследуем точку х = 0, найдем односторонние пределы:
Односторонние пределы существуют, но не равны, поэтому х = 0 – точка разрыва первого рода. Примеры для самостоятельной работы 1. Вычислить: а) в) д)
2. Исследовать на непрерывность функции: а)
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ Производная функции
Производной функции у = f (x) по аргументу х называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю: у¢ = Операция нахождения производной f ¢(x) называется дифференцированием. Геометрический смысл производной: производная f ¢(x0) есть угловой коэффициент касательной, проведенной к кривой f(x) в точке x0 , то есть k = tg a = f ¢(x0). Уравнение касательной имеет вид: у - f (x0) = f ¢(x0) (x - x0 ). Таблица производных и основные правила дифференцирования: 1. C ¢ = 0 2. (U + V) ¢ = U ¢ + V ¢ 3. (UV) ¢ = U ¢ V + U V ¢ 4. (CU) ¢ = C U ¢ 5. 7. (xn) ¢ = n x n-1 8. x ¢ = 1 9. 11. (a x) ¢ = a x ln a 12. (e x) ¢ = e x 13. (log a x)¢ = 15. (sin x) ¢ = cos x 16. (cos x) ¢ = – sin x 17. (tg x) ¢ = 19. (arcsin x) ¢ = 21. (arctg x) ¢ = Примеры: Найти производные функций: 1) у = х3 + 5е x + sin x. По формулам (2), (4), (7), (12), (15) имеем: у ¢ = (x3 + 5e x + sin x)¢ = (x 3)¢ + (5e x)¢ + (sin x)¢ = 3x2 + 5e x + cos x 2) y = (x4 - 6x2 + 1) ln x. По формулам (1) – (3), (7), (14) имеем у ¢ = (х4 -6х2 + 1)¢ ln x + (x4 -6x2 + 1) (ln x)¢ = (4x3-12x) ln x + + (x4 -6x2 +1)
Производная сложной функции
Если y есть функция переменной u, а переменная u есть функция переменной x, то y есть функция переменной x, то есть y = f (u), u = Производная сложной функции определяется по формуле: у ¢ = f ¢u ∙ u ¢x. (23) Примеры. Найти производные функций: 1) y = cos (x2). По формулам (23), (16), (7) имеем: у ¢= - sin (x2) (x2)¢= - sin (x2) 2x = - 2x ∙ sin(x2). 2) y = arctg (e 2x). По формулам (23), (21), (12), (4) имеем у ¢=
3) По формулам (23), (17), (9), (14), (16), (4) имеем
Производные высших порядков
Производная от производной y ¢= f ¢(x) называется второй производной, то есть y ¢¢ = (f ¢(x))¢ = f ¢¢(x). Производная n-ого порядка – это производная от производной (n - 1) порядка f (n) (x) = (f Пример. Найти производную второго порядка: у = е Находим первую производную у ¢= 3е 3х, затем у ¢¢ = (3е
Дифференциалы функции
Дифференциалом dy функции у = f (x) называется произведение производной этой функции на приращение независимой переменной Dх: dy = f ¢(x) Dx Так как dx = Dx, то dy = f ¢ (x) dx, поэтому f ¢(x) = Геометрически дифференциал функции есть приращение ординаты касательной, проведенной к графику функции у = f (x). Свойства дифференциала аналогичны свойствам производной. Дифференциалом второго порядка d2y функции у = f (x) называется дифференциал от дифференциала первого порядка этой функции d2y = d(dy) = f ¢¢(x) dx2. Пример. Найти дифференциалы функции: у = sin x. Найдем dy = f ¢(x) dx = cos x dx, затем d2y = d (dy) = – sinx dx2.
Правило Лoпиталя
Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует.
Пример.
Применили правило Лoпиталя дважды. Правило Лoпиталя позволяет раскрыть все виды неопределенностей и может быть применено несколько раз.
Примеры для самостоятельной работы 1. Найти а) у = (х2 - 3х + 5)4; б) у = arcsin e 5х; в) у = log 2. Найти dy функции: а) у = 2 sin (3x + 1); б) у = sin3(x + 3. Найти d2y: а) y = sin2x; б) 4. Найти пределы: а) в)
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.12.41 (0.007 с.) |

 ,
,  , ¥ - ¥, 0×¥, ¥0, 1¥, 00, которые появляются при подстановке предельного значения переменной. Нахождение предела функций в таких случаях называют раскрытием неопределенностей.
, ¥ - ¥, 0×¥, ¥0, 1¥, 00, которые появляются при подстановке предельного значения переменной. Нахождение предела функций в таких случаях называют раскрытием неопределенностей. ; 2)
; 2)  ; 3)
; 3)  .
.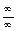 , разделим числитель и знаменатель на х с наибольшим показателем степени числителя и знаменателя.
, разделим числитель и знаменатель на х с наибольшим показателем степени числителя и знаменателя.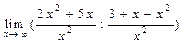 =
= 
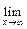
 = (
= (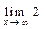 +
+ 
 ): (
): ( ) = =
) = = 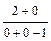 = - 2.
= - 2.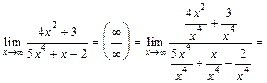



 является бесконечно малой величиной при
является бесконечно малой величиной при  , тогда
, тогда  является бесконечно большой величиной; числитель дроби
является бесконечно большой величиной; числитель дроби 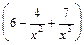 является функцией, предел которой равен 6 при
является функцией, предел которой равен 6 при  .
.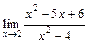 .
.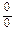 . Для раскрытия этой неопределенности разложим числитель и знаменатель дроби на множители.
. Для раскрытия этой неопределенности разложим числитель и знаменатель дроби на множители.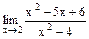 =
= 
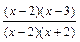 =
= 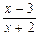 = -
= -  .
.
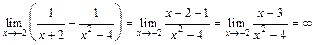 , т.к. знаменатель дроби (
, т.к. знаменатель дроби (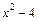 ) при
) при  является бесконечно малой величиной, тогда
является бесконечно малой величиной, тогда 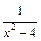 – бесконечно большая величина; числитель дроби (
– бесконечно большая величина; числитель дроби (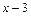 ) является функцией, предел которой при
) является функцией, предел которой при 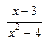 является бесконечно большой величиной при
является бесконечно большой величиной при 
 = 1.
= 1. =
=  (1+y)
(1+y) 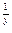 = e.
= e. .
. , воспользуемся первым замечательным пределом, умножим и разделим дробь на число 3.
, воспользуемся первым замечательным пределом, умножим и разделим дробь на число 3.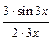 =
= 
 =
=  ×1 =
×1 =  .
.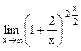 =
=  = e2.
= e2. ;
; f (x) = f (x0 ).
f (x) = f (x0 ).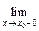 f(x) ≠
f(x) ≠ 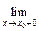 f (x), то х0 – точка разрыва первого рода.
f (x), то х0 – точка разрыва первого рода.
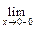 f (x) =
f (x) =  = -2,
= -2, f (x) =
f (x) =  = 0.
= 0. ; б)
; б)  ;
;
 ; г)
; г) 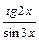 ;
; ; е)
; е)  ; ж)
; ж) 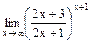 .
.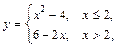 б)
б)  .
.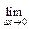
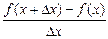 =
= 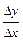 .
.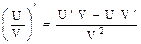 6.
6. 
 10.
10. 
 14. (ln x) ¢ =
14. (ln x) ¢ = 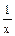
 18. (ctg x) ¢ =
18. (ctg x) ¢ = 
 20. (arccos x) ¢ =
20. (arccos x) ¢ = 
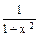 22. (arcctg x) ¢ =
22. (arcctg x) ¢ = 
 .
.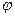 (x), y = f(u(x)) называется сложной функцией.
(x), y = f(u(x)) называется сложной функцией. (e 2x)¢=
(e 2x)¢=  e 2x (2x)¢ =
e 2x (2x)¢ =  .
.


 (x))¢.
(x))¢.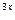 .
.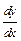 .
.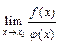 =
=  .
. =
=  =
= 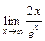 =
=  = 0.
= 0. (x - cos x).
(x - cos x).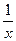 ).
).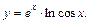
 ; б)
; б) 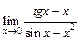 ;
; ; г)
; г)  .
.


