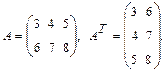Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы. Действия с матрицамиСодержание книги Поиск на нашем сайте
Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрицы обозначаются латинскими буквами А, В, С, … и записываются в виде:
или Две матрицы называются равными, если они имеют одинаковые размеры и равны все соответствующие элементы этих матриц, т.е. Am×n = Bm×n,если aij = bij для любых i=1, 2, …, m; j=1, 2, …, n. Матрицей (вектором) – строкой называется матрица, состоящая из одной строки:
Матрицей (вектором) – столбцом называется матрица, состоящая из одного столбца:
Матрица, у которой число строк равно числу столбцов (m=n), называется квадратной матрицей порядка n. Элементы матрицы aij, у которых номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицыа11, а22, …, аnn. Квадратная матрица, у которой все диагональные элементы равны 1, а остальные элементы равны 0, называется единичной матрицей n-го порядка, обозначается Е. Например, Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нулевой, обозначается О. Над матрицами можно производить следующие действия: 1. Умножение матрицы на число. При умножении матрицыА=(aij) на число λ каждый ее элемент умножается на это число λА=(λaij). Пример.
2. Сложение матриц. Суммой двух матриц А = (aij) и B = (bij) одинакового размера m×n называется матрица С размера m×n, С = А + B, сij = aij + bij для i = 1, 2, …, m; j =1, 2, …, n. Пример. Даны матрицы
Матрица 3. Вычитание матриц. Разность матриц А = (aij) и B = (bij) размера m×n есть матрица D размера m×n, элементы которой есть разность соответствующих элементов матриц А и В: D=А - В, dij = aij - bij для i =1, 2, …, m; j =1, 2, …, n. Пример.
4. Умножение матриц. Произведением матрицы Аm×k на матрицу Bk×n называется матрица Сm×n, каждый элемент которой сij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В. Аm×k·Bk×n=Сm×n, где cij = ai1 · b1j + ai2 · b2j +… + aik · bkj. При умножении матриц число столбцов (k) первой матрицы должно равняться числу строк второй матрицы. Вообще говоря, А × В ≠ В × А. Матрицы А и В называются перестановочными, если А × В = В × А.
Пример.
Пример.
Пример.
Пример.
5. Транспонирование матрицы. Матрица АТ, полученная из матрицы А заменой ее строк соответствующими столбцами, называется транспонированной. Если Аm×n, то Пример.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.88.132 (0.006 с.) |


 . Каждый элемент aij матрицы имеет два индекса i
. Каждый элемент aij матрицы имеет два индекса i  иj, которые показывают, что элемент находится в i-й строке и j-м столбце.
иj, которые показывают, что элемент находится в i-й строке и j-м столбце. .
. .
. – единичная матрица третьего порядка.
– единичная матрица третьего порядка.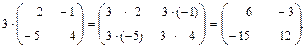
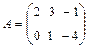 и
и  .
.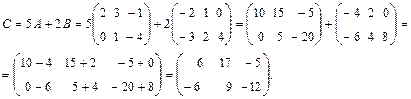
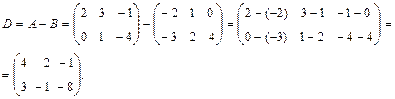



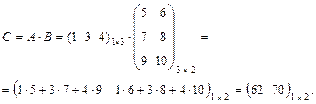

 .
.