
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Из этой системы обратным ходом метода Гаусса находимСодержание книги Поиск на нашем сайте
х4 = 1; х3 = 5 - 8х4 = 5 - 8×1 = - 3; х2 = х1 = 3+2х2 + 2х3 + 3х4 = 3 + 2×1 + 2×(-3) + 3×1 = 2. Ответ: (2; 1; -3; 1).
Задание 3. Даны координаты вершин треугольника АВС. Требуется найти: 1) длину стороны ВС; 2) уравнение линии ВС; 3) уравнение высоты, проведенной из точки А; 4) величину угла В; 5) проекцию вектора
А(2; -1)
С(-6; 5)
1) Найдем координаты вектора
Длина стороны ВС как длина вектора
2) Составим уравнение линии ВС, пользуясь каноническим уравнением прямой, М0(х0; у0) = С(5; 3),
2х + 11у - 43 = 0 - уравнение прямой ВС. 3) Составим уравнение высоты АЕ, зная точку А(2; -1) и условие перпендикулярности прямой
у - у0 = k(х - х0) - уравнение прямой, проходящей через данную т. М0(х0; у0) с угловым коэффициентом k. у -(- 1) = 11х - 2у - 24 = 0 - уравнение высоты АЕ. 4) Угол В образован векторами
a = ÐВ = arccos 5) Найдем проекцию
6) Находим уравнения сторон АВ и АС, используя каноническое уравнение. АВ: А(2; -1); или 4х - 3у - 11 = 0 уравнение прямой АВ. АС: А(2; -1); или 3х + 4у - 2 = 0 уравнение прямой АС. Для того, чтобы определить область треугольника АВС, находим полуплоскость относительно каждой стороны DАВС, подставляя в ее уравнение координаты соответствующей точки. ВС: 2х + 11у - 43 = 0, А (2; -1), имеем 2×2 + 11×(-1) - 43 = -50 < 0; АС: 3х + 4у - 2 = 0, В (5; 3), 3×5 + 4×3 - 2 = 25 > 0; АВ: 4х - 3у - 11 = 0, С (-6; 5), 4 (- 6) - 3×5- 11 = -50 < 0. Система неравенств, определяющая треугольник АВС:
Задание 4. Найти пределы функции, не применяя правило Лопиталя. а) разделили числитель и знаменатель дроби на х2,
в) = = Умножили числитель и знаменатель дроби на сопряженный множитель с) = По формуле половинного аргумента преобразовали числитель и воспользовались формулой 1-го замечательного предела.
Задание 5. Найти а)
=
= в) у = (х + 1) ×arctg
= arctg с) у = (х + ln sin х)3. Находим производную сложной функции у = f (u (x)),
= 3 × (x + ln sin x)2 × (1 + ctg x).
Задание 6. Исследовать функцию и построить ее график: 1) Находим область определения функции D: (-¥; 0) È (0; ¥). 2) Находим асимптоты графика: При х = 0 функция не определена. Найдем односторонние пределы при х®0:
следовательно, прямая х=0 – вертикальная асимптота. у = kx + b – наклонная асимптота, k= числитель и знаменатель дроби разделили на х3.
у = 2 - горизонтальная асимптота. 3) Точки пересечения с осями: При у = 0 имеем х1 = 0,5; х2 = -3. 4) Четность, нечетность: f (-x) = f (- x) ≠ f (x) и f (- x) ≠ - f (x), значит, функция f (x) не является ни четной, ни нечетной.
5) Возрастание, убывание, экстремумы:
у¢ = 0, то 6 - 5х = 0, х = 1,2; у¢ = ¥, х = 0 Ï D;
х = 1,2 точка максимума и f max = 6) Выпуклость, вогнутость, точки перегиба.
у¢¢ = 0, то 10х - 18 = 0; х = 1,8 у¢¢ = ¥; х = 0 Ï D.
График функции изображен на рисунке:
ВОПРОСЫ ДЛЯ ЭКЗАМЕНА
1. Матрица (квадратная, единичная, нулевая, треугольная), размер, порядок матрицы. 2. Действия с матрицами (умножение на число, сложение, вычитание, умножение, транспонирование). Свойства действий с матрицами. 3. Определители второго и третьего порядков. 4. Миноры и алгебраические дополнения. Теорема о разложении определителя по строке (столбцу). 5. Свойства определителей. 6. Обратная матрица. 7. Системы линейных уравнений. 8. Правило Крамера. 9. Метод Гаусса. 10. Ранг матрицы. 11. Теорема Кронекера-Капелли. 12. Определение вектора, линейные операции над векторами. 13. Проекция вектора на ось. Теоремы о проекциях. 14. Действия над векторами, заданными своими координатами. 15. Скалярное произведение векторов, его свойства. 16. Условия коллинеарности и перпендикулярности векторов. 17. Прямая линия на плоскости. Каноническое, общее уравнения прямой, уравнение прямой с угловым коэффициентом, уравнение прямой, проходящей через две точки. 18. Условия параллельности и перпендикулярности двух прямых. 19. Каноническое уравнение окружности, эллипса.
20. Каноническое уравнение гиперболы, параболы. 21. Предел функции в точке. 22. Бесконечно малая и бесконечно большие функции. Свойства бесконечно малых функций. 23. Основные теоремы о пределах. 24. Непрерывность функции, точки разрыва. 25. Производная функции. Геометрический смысл производной. 26. Дифференцируемость функции. Теорема о связи дифференцируемой и непрерывной функции. 27. Основные правила вычисления производных, таблица производных. 28. Производная сложной функции. 29. Производные высших порядков. 30. Дифференциал функции. Геометрический смысл дифференциала. 31. Правило Лопиталя. 32. Возрастание и убывание функции. Необходимое и достаточное условия экстремума. 33. Выпуклость, вогнутость кривой. Необходимое и достаточное условия существования точек перегиба. 34. Асимптоты графика функции. 35. Полная схема исследования функции.
СПИСОК ЛИТЕРАТУРЫ
ОГЛАВЛЕНИЕ
1. МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ............................................................................... 3 1.1. Матрицы. Действия с матрицами....................................................... 3 1.2. Свойства действий с матрицами......................................................... 7 1.3. Определители. Свойства определителей......................................... 7 1.4. Обратная матрица................................................................................. 12 1.5. Ранг матрицы.......................................................................................... 15 1.6. Системы линейных уравнений.......................................................... 17 1.7. Правило Крамера.................................................................................. 17 1.8. Метод Гаусса......................................................................................... 20 1.9. Теорема Кронекера-Капелли............................................................ 24 2. ВЕКТОРЫ НА ПЛОСКОСТИ.. 25 2.1. Векторы, линейные операции над векторами. 25 2.2. Проекция вектора на ось. Теоремы о проекциях. 27 2.3. Действия над векторами, заданными своими координатами..28 2.4. Скалярное произведение векторов, его свойства. 30 3. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ.. 34 4. КРИВЫЕ ВТОРОГО ПОРЯДКА.. 38 5. ВВЕДЕНИЕ В АНАЛИЗ. 42 5.1. Предел функции. Бесконечно малая и бесконечно большая функции. 42 5.2. Теоремы о пределах. 43 5.3. Раскрытие неопределенностей. Замечательные пределы.. 44 5.4. Непрерывность функции. 47 6. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ.. 49 6.1. Производная функции……………………………………………49 6.2. Производная сложной функции. 50 6.3. Производные высших порядков. 51 6.4. Дифференциалы функции. 51 6.5. Правило Лoпиталя. 52 6.6. Возрастание и убывание функции. Локальные экстремумы.. 53
6.7. Выпуклость, вогнутость кривой. Точки перегиба. 54 6.8. Асимптоты графика функции. 55 6.9. Полная схема исследования функции…………………………..55 7. ЗАДАЧИ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ.............................................. 58 8. ОБРАЗЕЦ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ... 66 9. ВОПРОСЫ ДЛЯ ЭКЗАМЕНА..................................................................... 75 СПИСОК ЛИТЕРАТУРЫ.................................................................................. 76
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.112 (0.009 с.) |

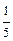 (-5 -9х3 - 17х4) =
(-5 -9х3 - 17х4) =  на вектор
на вектор  ; 6) систему неравенств, определяющих треугольник АВС. Сделать чертеж по координатам точек.
; 6) систему неравенств, определяющих треугольник АВС. Сделать чертеж по координатам точек.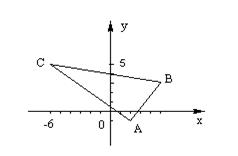
 В(5; 3)
В(5; 3)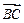
 .
. .
. , преобразуем его 2х - 10 = -11у + 33,
, преобразуем его 2х - 10 = -11у + 33, ,
, (х - 2) или 2у + 2 = 11х - 22,
(х - 2) или 2у + 2 = 11х - 22, , причем
, причем  ,
, - острый.
- острый. на
на  по формуле
по формуле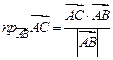 ,
,  =(3; 4).
=(3; 4). .
. ; 4х - 8 = 3у + 3
; 4х - 8 = 3у + 3 ; 6х - 12 = -8у -8
; 6х - 12 = -8у -8
 = 2,
= 2,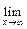
 ,
,  .
.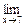
 =
= 



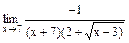 =
=  .
.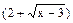 , затем разложили на множители, сократили на (х - 7).
, затем разложили на множители, сократили на (х - 7).
 =
= 
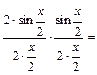
 .
.
 1,
1, 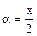 .
.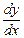 данных функций:
данных функций: . Находим производную частного функций:
. Находим производную частного функций: =
= =
= .
.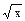 , находим производную произведения функций:
, находим производную произведения функций: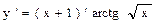 +
+ 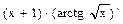 =
= = arctg
= arctg  .
. ,
,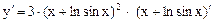 =
=  =
= .
. и
и  ,
, =
= 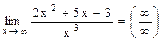 =
= 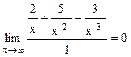 ,
,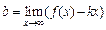 =
=  =
= 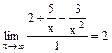 ,
, или
или  , отсюда
, отсюда
 ,
, ;
;
 .
. ,
,
 - точка перегиба графика функции.
- точка перегиба графика функции.



