
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ранг матрицы, система линейных уравнений. Теорема кронекера-капелли и следсвиеСодержание книги
Поиск на нашем сайте
Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров. Пример. В рассмотренной выше матрице
Две матрицы Можно показать, что следующие преобразования не меняют ранга матрицы: 1) перестановка строк матрицы; 2) умножение какой-либо строки на действительное число, отличное от нуля; 3) прибавление к элементам одной строки соответствующих элементов другой строки; 4) вычеркивание строки, все элементы которой равны нулю. Указанные преобразования можно использовать для определения ранга матрицы. ,. Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы. Если при этом ранг равен числу неизвестных, то система имеет единственное решение, если он меньше числа неизвестных, решений -множество. Пример. Исследовать систему линейных уравнений Решение. Поскольку все элементы матрицы системы входят в расширенную матрицу, то ранги обеих матриц можно вычислять одновременно. ~ Таким образом, матрица Линейные пространства Непустое множество L элементов I. Для любых двух элементов 1) x + y = y + x [коммутативность]; 2) x +(y + z)=(x + y)+ z [ассоциативность]; 3) в L существует такой элемент, что x +0= x для всех 4) для каждого [ Эти четыре свойства можно было высказать короче: в L введена операция сложения, превращающая L в абелеву группу.] II. Для любого числа
5) 6) 7) 8) В зависимости от того, какой запас чисел используется (все комплексные или только действительные), различают комплексные или действительные пространства. 14. линейная зависимость и независимость векторов линейного пространства Любой вектор плоскости Также говорят, что вектор Типовая вещь. Для того чтобы два вектора плоскости Пример 1 а) Проверить, коллинеарны ли векторы Решение: Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию Составим пропорцию из отношений соответствующих координат векторов: Сокращаем: Для двух векторов плоскости эквиваленты следующие утверждения: Соответственно, эквивалентны следующие противоположные утверждения: два вектора плоскости
а) Вычислим определитель, составленный из координат векторов
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.94.189 (0.01 с.) |

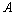 все миноры 3-го порядка равны нулю (это нетрудно проверить, миноров 3-го порядка всего десять), а среди миноров 2-го порядка есть отличные от нуля, например, вычисленный выше. Значит, ранг матрицы
все миноры 3-го порядка равны нулю (это нетрудно проверить, миноров 3-го порядка всего десять), а среди миноров 2-го порядка есть отличные от нуля, например, вычисленный выше. Значит, ранг матрицы 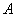 равен двум. Это обозначается:
равен двум. Это обозначается: 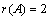 .
.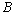 и
и 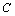 называются эквивалентными (пишут:
называются эквивалентными (пишут: 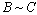 ), если их ранги равны:
), если их ранги равны: 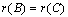 .
.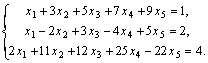

 ~
~ 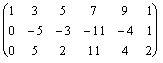 ~
~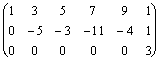 .
.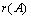 равен двум. В матрице
равен двум. В матрице 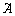 три ненулевых строки, ее ранг
три ненулевых строки, ее ранг 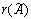 равен трем. А т.к.
равен трем. А т.к. 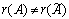 , система несовместна.
, система несовместна. произвольной природы называется линейным или векторным пространством, если оно удовлетворяет следующим условиям:
произвольной природы называется линейным или векторным пространством, если оно удовлетворяет следующим условиям: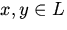 однозначно определен третий элемент
однозначно определен третий элемент 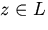 ,называемый их суммой и обозначаемый x + y, причем выполняются следующие свойства
,называемый их суммой и обозначаемый x + y, причем выполняются следующие свойства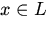 [существование нуля];
[существование нуля];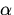 и любого элемента
и любого элемента  ,называемый произведением элемента x на число
,называемый произведением элемента x на число 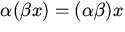 ;
;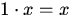 ;
;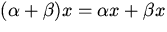 ;
; .
.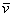 единственным образом раскладывается по базису
единственным образом раскладывается по базису 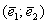 :
: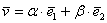 , где
, где 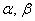 – действительные числа. Числа
– действительные числа. Числа 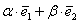 называют разложением вектора
называют разложением вектора  были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны
были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны 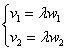 . По существу, это покоординатная детализация очевидного соотношения
. По существу, это покоординатная детализация очевидного соотношения  .
. .
. ?
?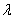 , такой, чтобы выполнялись равенства
, такой, чтобы выполнялись равенства  , значит, данные векторы коллинеарны.
, значит, данные векторы коллинеарны.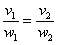 и посмотреть, будет ли она верной:
и посмотреть, будет ли она верной: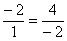
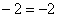 , таким образом, соответствующие координаты пропорциональны, следовательно,
, таким образом, соответствующие координаты пропорциональны, следовательно, 
 .
.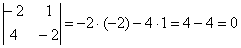 , значит, данные векторы коллинеарны.
, значит, данные векторы коллинеарны.


