
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраическая запись Комплексных чиселСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Алгебраическая запись Комплексных чисел
Сложение комплексных чисел
Вычитание комплексных чисел
Умножение комплексных чисел
Деление комплексных чисел
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Тригонометрическая форма записи комплексного числа, умножение деление возведение в степень. Формула Муавра
Однако более стандартно следующее правило: Если угол больше 180 градусов, то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла: 1) Если 2) Если 3) Если
Любое комплексное число (кроме нуля) Возведение комплексных чисел в степень
формула Муавра: Если комплексное число представлено в тригонометрической форме
3. Корень нной степени из комплексного числа. Геометрическая интерпретация
Рассмотрим уравнение
Подставляем в формулу значение Подставляем в формулу значение Подставляем в формулу значение
Очень часто полученные корни требуется изобразить геометрически: Теперь берем аргумент первого корня Берем аргумент второго корня По такому же алгоритму строится точка Легко заметить, что корни расположены геометрически правильно с интервалом
Логарифм комплексного числа, степень комплексного числа. Геом интерпретация
Натуральным логарифмом комплексного числа r (cosj + i sinj) называется показатель степени, в которую надо возвысить e, чтобы получить логарифмируемое число. Обозначив натуральный логарифм фимволом Log, можно сказать, что равенство
Log [ r (cosj + i sinj)] = x + yi равносильно следующему:
ex+yi = r (cosj + i sinj). Последнее равенство можно написать так:
ex (cos y + i sin y) = r (cosj + i sinj), откуда, сравнивая модули и аргументы, получим:
ex = r, y = j + 2 k p (k = 0, ±1, ±2,...), т.е.
x = log r и x + yi = log r + (j + 2 k p) i и окончательно
т.е. натуральный логарифм комплексного числа равен комплексному числу, вещественная часть которого есть обычный логарифм модуля, а мнимая часть представляет собою произведение i на одно из значений аргумента.
Определитель с нулевой строкой (столбцом) равен нулю Если строки (столбцы) определителя пропорциональны, то он равен нулю. Определитель с нулевой строкой (столбцом) равен нулю.
Система линейных уравнений теорема Крамера Запись систем линейных уравнений в матричной форме Линейные пространства Непустое множество L элементов I. Для любых двух элементов 1) x + y = y + x [коммутативность]; 2) x +(y + z)=(x + y)+ z [ассоциативность]; 3) в L существует такой элемент, что x +0= x для всех 4) для каждого [ Эти четыре свойства можно было высказать короче: в L введена операция сложения, превращающая L в абелеву группу.] II. Для любого числа 5) 6) 7) 8) В зависимости от того, какой запас чисел используется (все комплексные или только действительные), различают комплексные или действительные пространства. 14. линейная зависимость и независимость векторов линейного пространства Любой вектор плоскости Также говорят, что вектор Типовая вещь. Для того чтобы два вектора плоскости Пример 1 а) Проверить, коллинеарны ли векторы Решение: Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию Составим пропорцию из отношений соответствующих координат векторов: Сокращаем: Для двух векторов плоскости эквиваленты следующие утверждения: Соответственно, эквивалентны следующие противоположные утверждения: два вектора плоскости а) Вычислим определитель, составленный из координат векторов Определение Действительное линейное пространство E называется евклидовым, если каждой паре векторов I. II. III. IV. Число Длина вектора Свойства: 1) 2) 3) 4) Углом между векторами
Ортогональные векторы
Векторы Нормированные векторы Вектор Если Система векторов
называется ортонормированной. Во всяком пространстве
...............
Пронормировав каждый вектор
Угол между векторами Продолжаем выжимать полезные вещи из скалярного произведения. Снова посмотрим на нашу формулу А части поменяем местами: TRIPPLE VECT ОЙКИ МАТЬ ИХ 11.1. Правые и левые тройки векторов и системы координат. Определение. Три вектора называются упорядоченной тройкой (или просто трой- кой), если указано, какой из этих векторов является первым, какой - вторым и какой - третьим. При записи тройки векторов мы всегда будем располагать эти векторы в порядке их следования. Так, запись bac означает, что первым элементом тройки является вектор b, вторым - вектор a и третьим - вектор c. Определение. Тройка не компланарных векторов abc называется правой (левой), если выполнено одно из следующих трех условий: 1. если, будучи приведены к общему началу, эти векторы распо- лагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки; 2. если после приведения к общему началу вектор c располагает- ся по ту сторону от плоскости, определяемой векторами a и b, откуда кратчайший поворот от a к b кажется совершаю- щимся против часовой стрелки (по часовой стрелке); 3. если, находясь внутри телесного угла, образованного приведен- ными к общему началу векторами a, b, c, мы видим поворот от a к b и от него к c совершающимся против часовой стрелки (по часовой стрелке). Легко проверить, что условия 1, 2 и 3 эквивалентны между собой. Заметим также, что понятие правой и левой тройки теряет смысл для компланарных векторов. Если две тройки векторов либо обе являются правыми, либо обе являются левыми, то говорят, что эти тройки одной ориентации. В противном случае говорят, что рассматриваемые две тройки противоположной ориентации. Всего из трех векторов a, b и можно составить следующие шесть троек: abc, bca, cab, bac, acb, cba. Тройки abc, bca, cab - правые, а bac, acb, cba - левые.
Векторное произведение Векторным произведением вектора
Векторное произведение обозначается квадратными скобками:
Свойства векторного произведения:
27. Смешанным произведением трех векторов Геометрический смысл смешанного произведения: если тройка векторов Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах
Объем пирамиды, построенной на этой тройке векторов равен
1° 2° 3° Три вектора компланарны тогда и только тогда, когда 4° Тройка векторов является правой тогда и только тогда, когда 5° 6° 7° 8° 9° 10° Тождество Якоби: Если векторы
Угол между двумя прямыми Угол φ между двумя прямыми, заданными общими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
4. Условия параллельности двух прямых: а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k 1 = k 2. (8) б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
5. Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
Пересекающимися, скрещивающиеся, паралельные
32. прямая м плоскость. Угол между прямой и плоскость. Паралельность и перпендикулярность прямой и плоскости. Вазимное расположение прямой и плоскости Эллипс Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (бóльшая, чем расстояние между фокусами). Каноническое (простейшее) уравнение эллипса с центром в начале координат и с фокусами в точках где
Рис. 3
Если центр эллипса находится в точке Гипербола Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Уравнение гиперболы с центром в начале координат и с фокусами в точках где Коэффициенты Прямые
Рис. 4 Если центр гиперболы находится в точке Парабола Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой. Уравнение параболы с вершиной в начале координат имеет вид: где
Если вершина параболы находится в точке Теоремы о проекциях
Алгебраическая запись Комплексных чисел
Сложение комплексных чисел
Вычитание комплексных чисел
Умножение комплексных чисел
Деление комплексных чисел
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 898; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.151 (0.009 с.) |


 ,
, 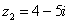

 ,
, 


 ,
, 


 ,
, 



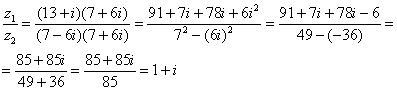
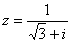

 , где
, где  – это модуль комплексного числа, а
– это модуль комплексного числа, а  – аргумент комплексного числа.
– аргумент комплексного числа. 
 стандартно обозначают:
стандартно обозначают:  Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.
Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем. .
. 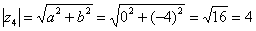 .
. 270 градусов:
270 градусов: 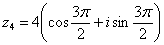 .
. 
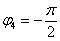 (минус 90 градусов),
(минус 90 градусов), 
 (1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле
(1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле  (2-ая координатная четверть), то аргумент нужно находить по формуле
(2-ая координатная четверть), то аргумент нужно находить по формуле  .
. (3-я координатная четверть), то аргумент нужно находить по формуле
(3-я координатная четверть), то аргумент нужно находить по формуле  .
.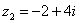
 Поскольку
Поскольку 

 , где
, где  :
: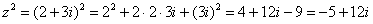

 справедлива формула:
справедлива формула:
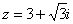 , найти
, найти 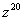 .
.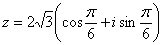

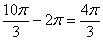






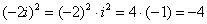


 ,
,  ,
,  ,
,  ,
, 


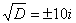


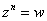 , или, то же самое:
, или, то же самое:  . Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при
. Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при  получается квадратный корень
получается квадратный корень  Уравнение вида
Уравнение вида  , которые можно найти по формуле:
, которые можно найти по формуле: , где
, где  – это модуль комплексного числа
– это модуль комплексного числа  ,
,  принимает значения:
принимает значения: 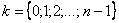


 ,
,  ,
, 


 ,
, 

 ,
, 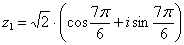
 , где
, где 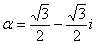
 Если
Если 
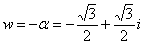
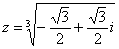
 ,
, 
 :
: 
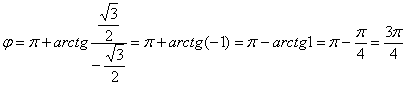
 ,
, 
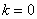 и получаем первый корень:
и получаем первый корень:
 и получаем второй корень:
и получаем второй корень: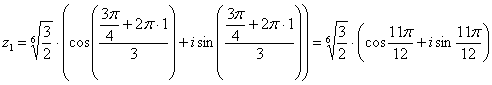
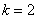 и получаем третий корень:
и получаем третий корень: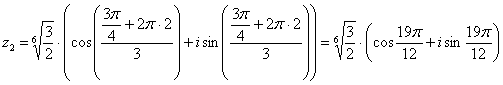

 и чертим циркулем окружность данного радиуса. Все корни будут располагаться на данной окружности.
и чертим циркулем окружность данного радиуса. Все корни будут располагаться на данной окружности. и выясняем, чему равняется угол в градусах:
и выясняем, чему равняется угол в градусах: 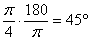 . Отмеряем транспортиром
. Отмеряем транспортиром  и ставим на чертеже точку
и ставим на чертеже точку 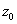 .
. и переводим его в градусы:
и переводим его в градусы:  . Отмеряем транспортиром
. Отмеряем транспортиром 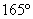 и ставим на чертеже точку
и ставим на чертеже точку  .
.

 .
. произвольной природы называется линейным или векторным пространством, если оно удовлетворяет следующим условиям:
произвольной природы называется линейным или векторным пространством, если оно удовлетворяет следующим условиям: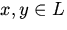 однозначно определен третий элемент
однозначно определен третий элемент 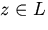 ,называемый их суммой и обозначаемый x + y, причем выполняются следующие свойства
,называемый их суммой и обозначаемый x + y, причем выполняются следующие свойства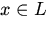 [существование нуля];
[существование нуля];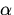 и любого элемента
и любого элемента  ,называемый произведением элемента x на число
,называемый произведением элемента x на число 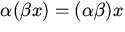 ;
;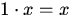 ;
;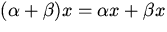 ;
; .
.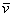 единственным образом раскладывается по базису
единственным образом раскладывается по базису 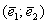 :
: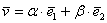 , где
, где 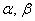 – действительные числа. Числа
– действительные числа. Числа 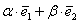 называют разложением вектора
называют разложением вектора  были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны
были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны 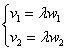 . По существу, это покоординатная детализация очевидного соотношения
. По существу, это покоординатная детализация очевидного соотношения  .
. .
. ?
?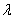 , такой, чтобы выполнялись равенства
, такой, чтобы выполнялись равенства  , значит, данные векторы коллинеарны.
, значит, данные векторы коллинеарны.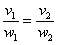 и посмотреть, будет ли она верной:
и посмотреть, будет ли она верной: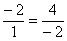
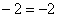 , таким образом, соответствующие координаты пропорциональны, следовательно,
, таким образом, соответствующие координаты пропорциональны, следовательно, 
 .
.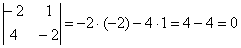 , значит, данные векторы коллинеарны.
, значит, данные векторы коллинеарны. сопоставляется число
сопоставляется число 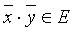 так, что
так, что  и
и  выполняются аксиомы:
выполняются аксиомы:



 называют скалярным произведением векторов
называют скалярным произведением векторов  и
и  ,
,  - скалярным квадратом вектора
- скалярным квадратом вектора 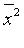 ). Введенная операция называется скалярным умножением векторов
). Введенная операция называется скалярным умножением векторов  - число
- число 


 (неравенство Коши-Буняковского);
(неравенство Коши-Буняковского); (неравенство треугольника).
(неравенство треугольника).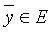 называют угол
называют угол  , для которого
, для которого
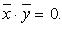

 то соответствующими этому вектору нормированными векторами будут
то соответствующими этому вектору нормированными векторами будут 
 для которой
для которой
 существует ортонормированный базис. Из произвольного базиса
существует ортонормированный базис. Из произвольного базиса  пространства
пространства 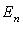 ортогональный базис может быть построен с помощью процесса ортогонализации:
ортогональный базис может быть построен с помощью процесса ортогонализации: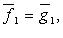
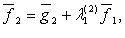 где
где 
 где
где 
 где
где 
 получим ортонормированный базис. В ортонормированном базисе (
получим ортонормированный базис. В ортонормированном базисе ( ) для векторов
) для векторов 
 имеем:
имеем:
 . По правилу пропорции сбросим длины векторов в знаменатель левой части:
. По правилу пропорции сбросим длины векторов в знаменатель левой части:

 на вектор
на вектор  называется третий вектор
называется третий вектор 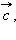 который обладает следующими свойствами:
который обладает следующими свойствами: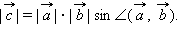
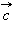 перпендикулярен к плоскости, в которой лежат вектора
перпендикулярен к плоскости, в которой лежат вектора 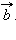
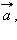
 и
и 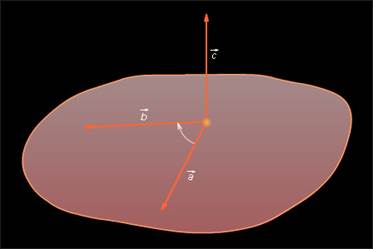
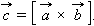
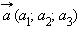 и
и 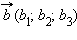 следующие
следующие 
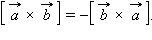
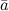 ,
, 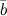 ,
, 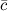 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 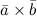 на вектор
на вектор 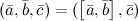
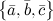 правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 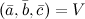 . В случае левой тройки
. В случае левой тройки 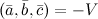 . Если
. Если 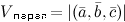

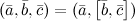
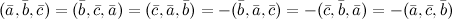
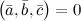
 . Если же
. Если же  , то векторы
, то векторы 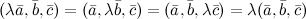
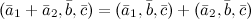


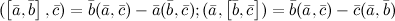

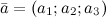 ,
,  и
и 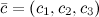 заданы своими координатами, то их смешанное произведение вычисляется по формуле
заданы своими координатами, то их смешанное произведение вычисляется по формуле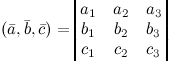


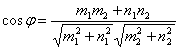



 (9)
(9)


 (10)
(10) и
и 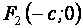 :
: (4)
(4) и
и  - полуоси эллипса, с – полуфокусное расстояние. Коэффициенты
- полуоси эллипса, с – полуфокусное расстояние. Коэффициенты  эллипса связаны соотношением
эллипса связаны соотношением 

 , то уравнение эллипса имеет вид:
, то уравнение эллипса имеет вид: (5)
(5) (6)
(6) и
и  гиперболы связаны соотношением
гиперболы связаны соотношением  .
. - асимптоты гиперболы.
- асимптоты гиперболы.
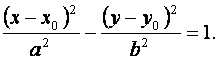 (7)
(7) , (8)
, (8)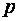 - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты
- расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты  .
.






