
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
п.7. Показательная форма записи комплексного числаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обозначение. Для " w Î R обозначим
Из равенства (1) и правил действия с комплексными числами, записанными в тригонометрической форме, следует справедливость следующей теоремы. Теорема 5. Для " u, w Î R, " n Î Z справедливы равенства: 1/ 2/ 3/ 4/ 5/ 6/ 7/ п.8. Связь между тригонометрическими И гиперболическими функциями Из формул Эйлера следует, что для
Складывая и вычитая эти равенства находим, что для
(1) (2) Как известно, из курса математического анализа, гиперболические косинус, синус, тангенс, котангенс, соответственно,
Если, в формулах (1), (2), заменить w на iw, то мы получим формулы для определения значений
П.9. Корни из комплексных чисел Определение. Пусть z Î C, n Î N. Комплексное число x называется корнем степени n из z, если
Теорема 6. Пусть n Î N, root (n) - множество всех корней степени n из 1. Тогда алгебра (root (n), ×, Доказательство. Пусть x, y Î root (n). Проверим, что умножение - бинарная операция. Имеем
Проверим, что
Очевидно, что 1 - корень степени n из 1. Доказано, что (root (n), ×, То, что алгебра (root (n), ×, Теорема 7. Для " n Î N существует точно n различных корней (1) Все корни расположены в вершинах правильного n - угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1,0). Доказательство. Проверим сначала, что числа
Докажем, что любой корень x степени n из 1 может быть вычислен по формуле (1). Т. к. x ¹ 0, то x можно записать в показательной форме
Имеем
Поэтому
где t Î Z. По теореме о делении с остатком, существуют такие q, r Î Z, что t = nq + r, где 0 £ r < q. Значит
т.е. x вычисляется по формуле (1). Изобразив числа, заданные формулой (1), на комплексной плоскости, мы увидим, что они расположены в вершинах правильного n - угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1,0). В частности, числа заданные формулой (1), попарно различны. n Теорема 8. Пусть n Î N, z Î C, z ¹ 0, (2) Доказательство. Проверим сначала, что числа
Пусть
Следовательно
Из выше доказанного следует, что числа
П.10. Мультисекция Теорема 1. (о мультисекции многочлена) Пусть
- многочлен с числовыми коэффициентами, q Î N
где Доказательство. Для m = 1 равенство (1) очевидно выполнено. Докажем (1) для m > 1. Имеем
Если
Если
Поэтому в (2) суммирование нужно вести только по тем r для которых Заметим, что равенство (1) справедливо не только для многочленов, но и для рядов.
Следствие 1. Пусть n, m Î N, q Î N
Доказательство. Рассмотрим многочлен
Применяя мультисекцию к многочлену
где
Имеем
Приравнивая действительные части обеих частей равенства (4) получаем равенство (3). n
П.11. Упорядоченные поля
Определение. Упорядоченным полем называется алгебраическая система (P, +, ×, -, 0, 1, £) такая, что: 1/ алгебра (P, +, ×, -,0, 1) - поле; 2/ £ - линейный порядок на P; 3/ для " a, b, c Î P a £ b ® a + c £ b + c; 4/ для " a, b Î P a £ b Ù c > 0 ® ac £ bc. n Другими словами, упорядоченное поле - это поле на множестве элементов которого определён линейный порядок £ согласованный, условиями 3/,4/, с операциями сложения и умножения. Нетрудно проверить, что для упорядоченного поля выполнены обычные свойства неравенств, известные для действительных чисел. Примерами упорядоченных полей являются поле рациональных и поле действительных чисел. Теорема 9. Если (P, +, ×, -,0, 1, £) - упорядоченное поле, то для " a Î P из условия a ¹ 0, следует, что a Доказательство. Т.к. £ - линейный порядок, то a > 0 или a < 0. Если a > 0, то, по условию 4/, a = (- a) (- a) > 0. n Теорема 10. Если (P, +, ×, -,0, 1, £) - упорядоченное поле, то для " a, b Î P из условия a ¹ 0 Ù b ¹ 0 следует, что a 2 + b 2 ¹ 0. Доказательство. Из теоремы 9 следует, что a Теорема 11. Поле комплексных чисел (C, +, ×, -, 0, 1) нельзя упорядочить. Доказательство. Предположим противное - поле комплексных чисел (C, +, ×, -, 0, 1) упорядоченно. Т.к. 1 ¹ 0, i ¹ 0, то, по теореме 10, 1 Задачник.
1. Найти действительную и мнимые части комплексных чисел:
Решение.
2. Найти a, b Î R, если:
2.1. 2.3.
Решение примера 2.2. Запишем левую часть равенства в алгебраической форме
Приравнивая действительную и мнимую части чисел в левой и правой частях равенства получим систему линейных уравнений
Прибавим к первому уравнению второе, умноженное на (-3), прибавим ко второму уравнению первое, умноженное на (-4), получим
3. Вычислить:
3.1. 3.2. ( 3.3. 3.4. 3.5.
Решение примера 3.6. Имеем
4. Вычислить:
4.1. 4.2. 4.3. 4.4.
Решение примера 4.2. Имеем
5. Вычислить:
5.1. 5.3. 5.5.
Решение примера 5.4. Имеем
6. Вычислить:
6.1.
6.3.
Решение примера 6.1. Разделим, по теореме о делении с остатком, число n на 4, получим, что
Ответ:
7. Вычислить:
7.1. 7.5.
Решение примера 7.2. Имеем
8. При каких z
8.1. Re (z 8.2. Im (z 8.3. Re (z
Решение примера 8.1. Запишем z
9. Найти значение f (x):
9.1.
Решение примера 9.1. Имеем
10. Доказать, что:
10.1. 10.1.
Решение примера 10.1. Имеем
Найти корни квадратного уравнения
Решение. Перепишем уравнение в виде
Выделим полный квадрат в левой части и перенесём свободный член в правую часть
Перепишем последнее уравнение в виде
Обозначим через u какой-нибудь квадратный корень из
Последнее равенство запишем в виде
12. Какие необходимые и достаточные условия для того, чтобы квадратное уравнение
Решение первого примера. Пусть x
Поэтому b / a, c / a Î R. Квадратное уравнение запишем в виде
Последнее уравнение имеет действительные корни если
Ответ:
13. Решить над C квадратные уравнения:
13.1. x 13.2. 2 x 13.3. 3 x 13.4. x 13.5. x
Решение примера 13.1. Имеем
Решение примера 13.6. Имеем
Обозначим
где
Приравнивая действительные и мнимые части чисел расположенных в левой и правой частях равенства получим систему уравнений
Имеем
Решая последнее уравнение находим, что
Отсюда следует, что
14. Найти z Î C,удовлетворяющие уравнению:
14.1. (i - z)(1 + 2 i) + (1 - iz)(3 - 4 i) = 0; 14.2. (- i + z)(1 - 2 i) + (1 + iz)(3 + 4 i) = 0.
Решение примера 14.1. Имеем
(-1-2 i - i (3-4 i)) z + (i (1+2 i) + (3-4 i)) = 0, (-5-5 i) z + (1-3 i) = 0,
15. Вычислить:
15.1.
15.2. 15.3. 15.4. 15.5. 15.6. 15.7. 15.8.
Решение примера 15.1. Имеем
16. Для n Î N, вычислить:
16.1. 16.3. Решение примера 16.1. Имеем
17. Пусть z = a + bi, где a, b Î R. Выразить через a, b:
17.1. z + ` z; 17.2. z -` z; 17.3. z 17.5.(1 / z) - (1 /` z); 17.6. (1 / z 17.7. (1 / z
Решение примера 17.7. Имеем
18.Решить уравнения:
18.1. (1 - i)` z - 3 iz = 2 - i; 18.2. z`z - 2` z = 3 - i; 18.3. z`z + 3(z -` z) = 4 +3 i; 18.4. z`z + 3(z +` z) = 3 i; 18.5. | (z - 12) / (z - 8 i) | = 5/3; 18.6. | (z - 4) / (z - 8) | = 1.
Решение уравнения 18.1. Запишем z в алгебраической форме z = a + bi, где a, b Î R. Уравнение перепишем в виде (1- i)(a - bi) - 3 i (a + bi) = 2 - i. Запишем левую часть в алгебраической форме (a - b + 3 b) + (- a - b - 3 a) i = 2 - i. Приравнивая действительные и мнимые части получим систему уравнений
Решая эту систему находим, что a = 0, b = 1, z = i. n
19. Следующие числа изобразить на комплексной плоскости:
1; -1; 0; 4; -4; i; - i; 2 i; -2 i; 1 + i; 1 - i; -1 + i; -1 - i;
20. Вычислить модули всех чисел из задачи 19.
21. Вычислить аргументы всех чисел из задачи 19.
22. Какие части плоскости заданы условиями:
22.1. Re z = 3; 22.2. Im z > 0; 22.3. Re z £ -2; 22.2. Im z = -2; 22.5. Im z £ 1; 22.6. Re z > -3; 22.7. Re z > 0 Ù Im z £ 0; 22.8. Re z £ -2 Ù Im z > -3; 22.9. 0 £ Re z < 2 Ù -1< Im z < 1?
23. Какие части плоскости заданы условиями:
23.1. | z | = 1; 23.2. | z | £ 2; 23.3. | z | > 3; 23.4. | z - 1 | = 1; 23.5. | z + i | < 1 Ù | z - i | > 2; 23.6. | z + 1 + i | > 2; 23.6. | z + i | £ 1 Ù | z - i | £ 2; 23.8. Re z > 0 Ù | z | £ 3; 23.9. | z - 1 - i | + | z | = 2; 23.10. | z - 2 | + | z + 2 | = 2; 23.11. | z - 2 | + | z + 2 | > 2?
24. Какие части плоскости заданы условиями:
24.1. -p / 4 < arg z < p / 4; 24.2. -p / 4 < arg (z - i) < p / 4; 24.2. | z | = arg z; 24.4. Re z + Im z < 1; 24.5. | z - 1 | ³ 2| z - i |; 24.3. Im ((z - z 24.4. Re (1 / z) = 1; 24.8. Im (1 / z) = 1; 24.9. Re (z 24.5. Im (z 2) = 1; 24.11. | (z - z 24.12. arg ((z - z
25. Дайте геометрическую интерпретацию следующих отображений:
25.1. z ® ` z; 25.2. z ® iz; 25.3. z ® i`z; 25.2. z ® - i`z; 25.5. z ® - z; 25.6. z ® 2 z. Решение примера 25.1. В лекциях проверено, что это отображение является симметрией относительно оси действительных чисел. n
26. Доказать тождества:
26.1. | z
26.2. Дайте геометрическую интерпретацию тождества 26.1.
26.3. | 1 - ` z
Решение примера 26.1. Имеем
n
Решение примера 26.2. Использую геометрическую интерпретацию комплексных чисел векторами плоскости получаем: сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин всех его сторон. n
27. Пусть
Обобщить это равенство на случай n комплексных чисел равного модуля.
28. Доказать, что для " a Î R, a > 0, " z Î C, z ¹ - a
| a + z | / | 1 + (` z / a) | = a.
Решение. Имеем
n
29. Доказать, что для " z
| (z
Решение. Пусть | z
Случай | z
30. Для каких z
30.1. | z 30.2. | z
Решение примера 30.1. Изображая числа векторами плоскости получаем, что равенство | z
31. Доказать неравенства:
31.1. Если | z | < 1 / 2, то | (1 - i) z 31.2. Если | z | < 1, то | z |

 . n (1)
. n (1) Равенство (1) называют формулой Эйлера. При этом обозначении, запись комплексного числа z ¹ 0, z = | z | (cos w + i sin w) в показательной форме принимает вид
Равенство (1) называют формулой Эйлера. При этом обозначении, запись комплексного числа z ¹ 0, z = | z | (cos w + i sin w) в показательной форме принимает вид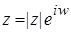 .
.  (2)
(2)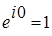 ;
;

 ;
;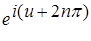
 ;
;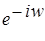
 ;
;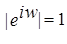 ;
; 

 ;
;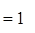
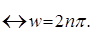 n
n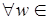 R
R
 ;
;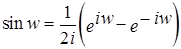 .
. , для
, для 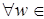 R, определяются равенствами:
R, определяются равенствами: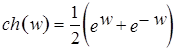 ;
; 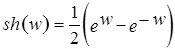 ;
;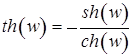 ;
; 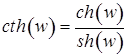 .
.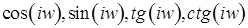 . Эти формулы выражают гиперболические формулы через тригонометрические. Для
. Эти формулы выражают гиперболические формулы через тригонометрические. Для  ;
; 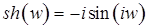 ;
;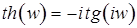 ;
; 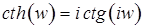 .
.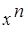
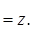 n
n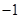 , 1) - группа, (которая называется группой корней степени n из 1).
, 1) - группа, (которая называется группой корней степени n из 1).

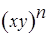
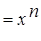


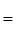
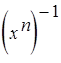
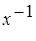 - корень степени n из 1.
- корень степени n из 1.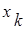 степени n из 1,
степени n из 1,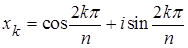 ,
,  .
.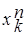
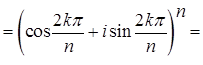

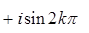
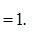
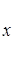
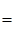

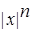
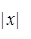
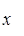


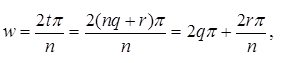

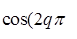
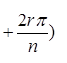
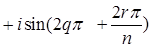
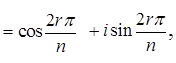
 Тогда существует точно n различных корней
Тогда существует точно n различных корней  степени n из z,
степени n из z,
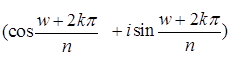 ,
, 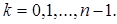
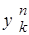
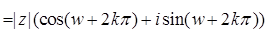
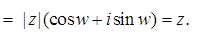
 - корень степени n из z. Докажем, что он вычисляется по формуле (2). Рассмотрим число
- корень степени n из z. Докажем, что он вычисляется по формуле (2). Рассмотрим число 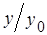 ,где
,где 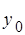 определено формулой (2). Имеем
определено формулой (2). Имеем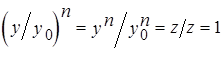 .
. . Имеем
. Имеем


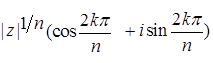
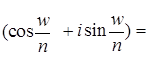
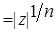
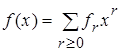
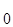 , m Î N, 0£ q < m. Тогда
, m Î N, 0£ q < m. Тогда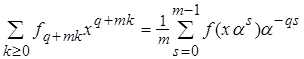 , (1)
, (1)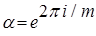 .
.
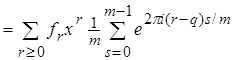 . (2)
. (2)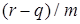 - целое, то
- целое, то  и
и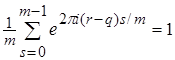 .
.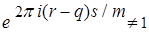 и по формуле суммы членов геометрической прогрессии
и по формуле суммы членов геометрической прогрессии
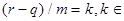 N
N  . (3)
. (3)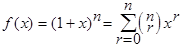 .
.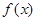 получим, что
получим, что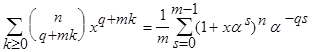 ,
,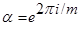 . Полагая x = 1 в последнем равенстве получим, что
. Полагая x = 1 в последнем равенстве получим, что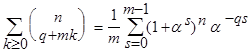 . (4)
. (4)
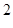 > 0.
> 0.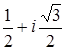
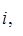
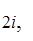

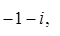

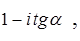
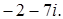
 n
n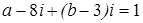 ; 2.2.
; 2.2. 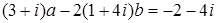 ;
;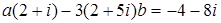 ; 2.4.
; 2.4. 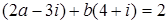 .
.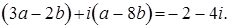

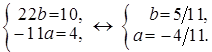 n
n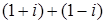 ; 3.6.
; 3.6. 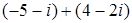 ;
;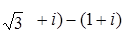 ;
;  ;
;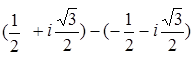 ; 3.8.
; 3.8. 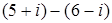 ;
;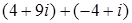 ; 3.9.
; 3.9. 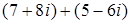 ;
; ; 3.10.
; 3.10. 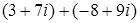 .
. n
n ; 4.5.
; 4.5. 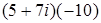 ;
;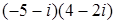 ; 4.6.
; 4.6. 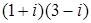 ;
;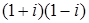 ; 4.7.
; 4.7. 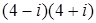 ;
; ; 4.8.
; 4.8. 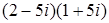 .
.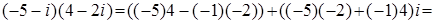
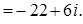 n
n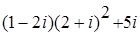 ; 5.2.
; 5.2. 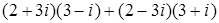 ;
;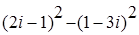 5.4.
5.4.  ;
;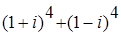 ; 5.6.
; 5.6.  .
.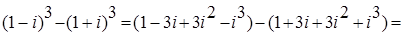
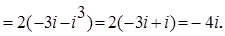 n
n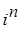 , где n Î N; 6.2.
, где n Î N; 6.2. 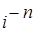 , где n Î N;
, где n Î N;

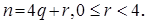 Имеем
Имеем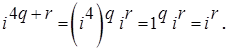
 , где r - остаток при делении n на 4. n
, где r - остаток при делении n на 4. n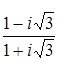 ; 7.2.
; 7.2. 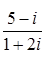 ; 7.3.
; 7.3. 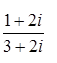 ; 7.4.
; 7.4. 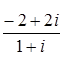
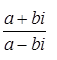 ; 7.6.
; 7.6. 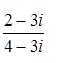 ; 7.8.
; 7.8. 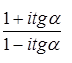 .
.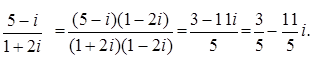 n
n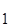 , z
, z 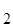 Î C:
Î C: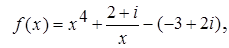 при x = 1 - 2 i;
при x = 1 - 2 i;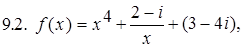 при x = 1 + 2 i.
при x = 1 + 2 i.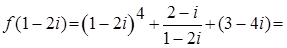
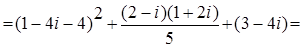

 n
n ;
;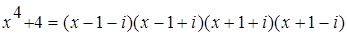 .
.
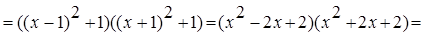
 n
n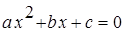 , где a, b, c Î C.
, где a, b, c Î C.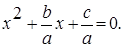
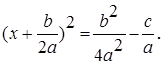
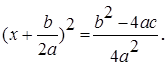
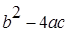 . Тогда
. Тогда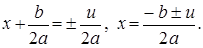
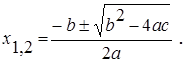 n
n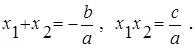
 .
.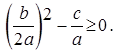
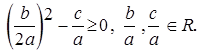 n
n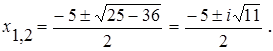
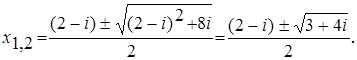
 ,
, Возводя в квадрат последнее равенство получим, что
Возводя в квадрат последнее равенство получим, что
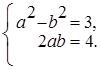
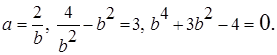
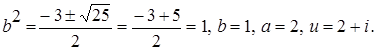
 n
n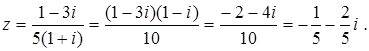 n
n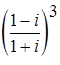 ;
;  ;
;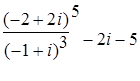 ;
;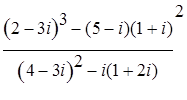 ;
;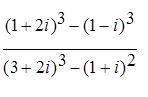 ;
; ;
;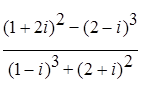 ;
;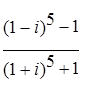 .
. n
n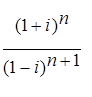 ; 16.2.
; 16.2.  ;
;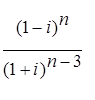 ; 16.4.
; 16.4. 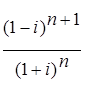 .
. . n
. n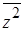 );
);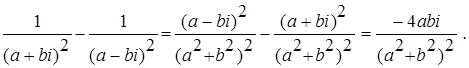 n
n
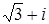 ;
; 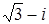 ;
;  ;
; 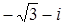 ;
;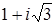 ;
; 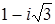 ;
; 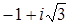 ;
; 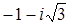 .
.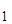 + z
+ z 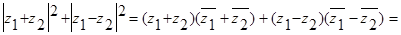
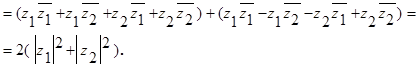
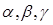 - комплексные числа,
- комплексные числа, 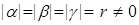 . Доказать, что
. Доказать, что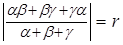 .
.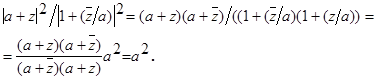

 - i z | < 3 / 4;
- i z | < 3 / 4;


