

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Выполнение арифметических операций над числами, представленными с фиксированной запятой.
Похожие статьи вашей тематики
Основной особенностью различных методов выполнения арифметических операций является то, что любая операция (сложение, вычитание, умножение, деление и др.) сводится к некоторой последовательности микроопераций, таких как:
- сложение
- сдвиг
- передача
- преобразование кодов.
Сложение выполняется по правилам сложения чисел в позиционных системах счисления.
То есть эта операция выполняется поразрядно, а возникающий в младших разрядах перенос направляется в старшие разряды.
Пример:
0,101101 1-ое слагаемое +0,000101 2-ое слагаемое ________ 0,101000 сумма 0,00101 перенос ________ 0,100010 сумма 0,01 перенос ________ 0,110010 сумма Операции сложения производятся одновременно над всеми разрядами двух слагаемых и продолжаются до тех пор, пока возникают переносы. Возникающие переносы приводят к продолжению операции. Это одна из особенностей позиционных систем. Видим, что собственно операция определения частичной суммы слагаемых выполняется в один приём, а возникающие переносы распространяются на всё более старшие разряды.
Сдвиг
Различают два вида микрооперации сдвига:
- логический сдвиг;
- арифметический сдвиг;
Логический сдвиг приводит к смещению всех разрядов числа, включая и знак, влево или вправо. При этом освобождающиеся разряды заполняются нулями или единицами.
Арифметический сдвиг выполняется над частью числа, часть сдвинутых разрядов теряется. (Очевидно, знаковый разряд должен исключаться из рассмотрения).
Передача.
Эта микрооперация предполагает, что некоторый код (число) записывается в соответствующее устройство и вытесняет тот код, который там находился до передачи.
Различают два вида передач:
- запись (с разрушением ранее записанной информации);
- чтение (без разрушения).
Преобразование.
Функция, выполняемая над передаваемыми числами, называется преобразованием. Чаще других в арифметических основах рассматривают инвертирование кода. Это поразрядная микрооперация yi = xi  1 (1 1 (1  i i  n), которая выполняется над всеми разрядами одновременно. n), которая выполняется над всеми разрядами одновременно.
Коды, применяемые для изображения отрицательных чисел.
Основное неудобство построения устройств, реализующих арифметические операции, состоит в сложном характере алгоритма вычитания. Для его преодоления в ЭВМ всегда операция выполняется по иным правилам, чем это делается обычно. В его основе лежит операция сложения. Алгоритмы выполнения такого рода операций требуют специальных кодов представления отрицательных чисел.
Прямой код.
Это естественное и наиболее привычное представление числа в следующем виде:
знак:
"+" соответствует 0
"-" соответствует 1
В цифровых разрядах пишется модуль положительного или отрицательного числа.
[X]пк - обозначим таким образом изображение числа "X" в прямом коде.
 Рассмотрим диапазоны представляемых чисел:
X+min = 0,000....0 - изображение положительного нуля
X+max = 0,111....1 = 1 - 2-n
X-min = 1,111....1 = -(1-2-n)
X-max = 1,000....0 - изображение отрицательного нуля.
Таким образом, нуль имеет двоякое изображение.
Замечания:
Рассмотрим диапазоны представляемых чисел:
X+min = 0,000....0 - изображение положительного нуля
X+max = 0,111....1 = 1 - 2-n
X-min = 1,111....1 = -(1-2-n)
X-max = 1,000....0 - изображение отрицательного нуля.
Таким образом, нуль имеет двоякое изображение.
Замечания:
- перед выполнением операции вычитания чисел с одинаковыми знаками и сложения с разными, необходимо сравнить по модулю два кода и, если нужно, сделать перестановку кодов местами, затем можно выполнять собственно операцию вычитания кодов.
- при выполнении операции умножения отдельно и независимо находятся модули произведений кодов, а знак находится как результат операции сложения по модулю два:
3. [X]пк * [Y]пк = sign Z. |Z||Z| = |X|*|Y| sign Z = sign X  sign Y или Sz = Sx sign Y или Sz = Sx  Sy
Собственно умножение выполняется с применением микроопераций сложения и сдвига. Sy
Собственно умножение выполняется с применением микроопераций сложения и сдвига.
- аналогично умножению выполняется операция деления с использованием микроопераций вычитания и сдвига.
Вследствие ряда неудобств в ЭВМ операции вычитания, сложения чисел с разными знаками и деления в прямом коде практически не выполняются.
Дополнительный код
Дополнительным называется код, в котором для положительного числа в знаковом разряде пишется "0", в цифровых - модуль числа, а для отрицательного в знаковом разряде пишется "1", в цифровых - дополнение числа до единицы.
 Если некоторое X- = -0,x1x2...xn нужно представить в дополнительном коде, то
Если некоторое X- = -0,x1x2...xn нужно представить в дополнительном коде, то
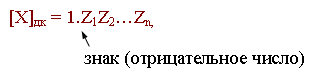 где: 1 - 0,x1x2...xn = 0, Z1Z2...Zn
Диапазоны представленных чисел:
Х+ min = 0,0...0 - положительный нуль
Х+ max = 0,11...1 = 1-2-n - максимальное положительное число.
X- min = 1,11...1 = 2-2-n - минимальное отрицательное число
X- max = 1,0...0 - наибольшее(по модулю) отрицательное число
Таким образом, нуль имеет единственное представление.
В самом деле, так как
X-X = [X+]дк + [X-]дк = 0, то в дополнительном коде: |X+| + 10 - |X-| = 10, если в разрядной сетке ЭВМ нет второго знакового разряда, то это переполнение теряется, и в знаковом разряде будет только нуль.
Важная особенность в получении дополнительного кода отрицательного числа состоит в следующем:
где: 1 - 0,x1x2...xn = 0, Z1Z2...Zn
Диапазоны представленных чисел:
Х+ min = 0,0...0 - положительный нуль
Х+ max = 0,11...1 = 1-2-n - максимальное положительное число.
X- min = 1,11...1 = 2-2-n - минимальное отрицательное число
X- max = 1,0...0 - наибольшее(по модулю) отрицательное число
Таким образом, нуль имеет единственное представление.
В самом деле, так как
X-X = [X+]дк + [X-]дк = 0, то в дополнительном коде: |X+| + 10 - |X-| = 10, если в разрядной сетке ЭВМ нет второго знакового разряда, то это переполнение теряется, и в знаковом разряде будет только нуль.
Важная особенность в получении дополнительного кода отрицательного числа состоит в следующем:
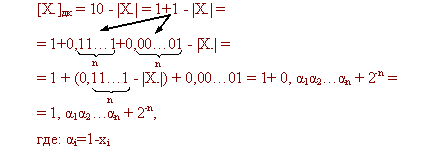 Таким образом, для записи дополнительного кода отрицательного числа необходимо в знаковом разряде поставить единицу, проинвертировать все цифровые разряды числа и прибавить единицу в младший разряд. Это также правило перевода из дополнительного кода в прямой код.
Рассмотрим на примерах выполнение операции сложения двух чисел с разными знаками.
Возможны следующие случаи:
Таким образом, для записи дополнительного кода отрицательного числа необходимо в знаковом разряде поставить единицу, проинвертировать все цифровые разряды числа и прибавить единицу в младший разряд. Это также правило перевода из дополнительного кода в прямой код.
Рассмотрим на примерах выполнение операции сложения двух чисел с разными знаками.
Возможны следующие случаи:
- X+ + Y+ = S+
- X+ + Y- = S+
- X+ + Y- = S-
- X- + Y- = S-
Необходимо помнить, что нельзя, выполняя операции, выходить за диапазон представляемых в данной разрядной сетке чисел, записанных с фиксированной запятой.
Положим n = 3, 1 - знаковый разряд и 2 - цифровых.
1. X+ = 0,10 2. Y+ = 0,01 3. В дополнительном коде
 То есть, нет никаких особенностей.
4. X+ = 0,105. Y- = -0,01 6. В дополнительном коде
То есть, нет никаких особенностей.
4. X+ = 0,105. Y- = -0,01 6. В дополнительном коде
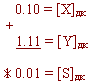 Переполнение теряется и получается верный результат.
7. X+ = 0,018. Y- = -0,11 9. В дополнительном коде
Переполнение теряется и получается верный результат.
7. X+ = 0,018. Y- = -0,11 9. В дополнительном коде
 10. X- = -0,1011. Y- = -0,01 12. В дополнительном коде
10. X- = -0,1011. Y- = -0,01 12. В дополнительном коде
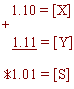 Возникающее переполнение теряется и общий результат отрицательный.
Таким образом, важной особенностью дополнительного кода является то, что знаковый разряд в процессе выполнения операции рассматривается совместно с цифровыми. Возникающие переносы теряются и не влияют на результат операции.
Возникающее переполнение теряется и общий результат отрицательный.
Таким образом, важной особенностью дополнительного кода является то, что знаковый разряд в процессе выполнения операции рассматривается совместно с цифровыми. Возникающие переносы теряются и не влияют на результат операции.
| 
|
Обратный код
Обратным называется код, для которого в знаковом разряде положительного числа пишется "0", в цифровых - модуль числа, а для отрицательного - в знаковом разряде пишется единица, в цифровых - инвертированные разряды исходного числа.
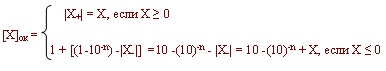
Определим диапазоны чисел:
X+ min = 0,00...0 - положительный нуль.
X+ max = 0,111...1 = 1 - 2-n
X- min = 1,11...1 0 = 2 - 2-n+1
X- max = 1,00...00 = 1
В обратном коде есть два изображения нуля:
"Положительный" нуль:
[X]ок = 0,0...0 и "отрицательный" нуль:
[X]ок = 1,11...11 При этом
X - X = [X+]ок + [X-]ок = |X+| + 10 - (10)-n - |X-| = +10 - (10)-n = 0 То есть, единица переноса в знаковом разряде эквивалентна единице младшего разряда. Поэтому при выполнении операции сложения-вычитания необходимо возникающий перенос циклически прибавлять в младший разряд частичного результата.
Рассмотрим прежние четыре случая, помня о том, что сумма двух слагаемых по модулю должна быть меньше единицы.
1. X+ = 0,102. Y- = -0,01 3. X+ + Y- = S+ 4. В обратном коде:

Возникающее переполнение должно быть добавлено к младшему разряду частичной суммы.
5. X+ = 0,106. Y+ = +0,017. X+ + Y+ = S+ 8. В обратном коде:

Нет никаких особенностей по сравнению с прямым кодом.
9. X+ = 0,0110. Y- = -0,1011. X+ + Y- = S- 12. В обратном коде:

То есть, не возникает циклического переноса.
13. X- = -0,01 14. Y- = -0,10 15. X- + Y- = S- 16. В обратном коде:

Возникает переполнение знакового разряда, которое добавляется в младший разряд частичной суммы.
Заметим, что получение обратного кода проще, чем дополнительного. Это поразрядно выполняемая микрооперция инверсии кода. Как станет ясно из схемного решения, эта микрооперация выполняется так же быстро, как и передача кода.
Поскольку результатом операции является совокупность результатов по всем разрядам, то данную операцию можно выполнять одновременно над всеми цифровыми разрядами числа.
| 8. Лекция: Модифицированные коды
| 
| 
| 
| | Страницы: 1 | 2 | 3 | вопросы |»
| | учебники | для печати и PDA | ZIP
| 
| | Если Вы заметили ошибку - сообщите нам, или выделите ее и нажмите Ctrl+Enter
| 
| | В лекции описаны модифицированный дополнительный и обратный коды. Даны методы умножения чисел с фиксированной запятой в прямом и дополнительном кодах, а также алгоритмы сдвига.
| 
| 
| 
| Важная особенность рассмотренных кодов состоит в том, что в процессе выполнения операции сложения-вычитания не происходит переполнения цифровой части числа и переноса в знаковый разряд. Переполнение возникает лишь в знаковом разряде. Так бывает потому, что сумма двух слагаемых по модулю меньше единицы.
При решении реальных задач часто трудно определить заранее, будет ли сумма двух слагаемых меньше единицы. Во всяком случае, для предотвращения переполнения можно вводить дополнительные ограничения на величину слагаемых, сужающих диапазон чисел, с которыми оперирует машина. И то, и другое является неприемлемым.
Рассмотрим такой пример:
X = -0,101 Дополнительный код 1.011 = [X]дк
Y= -0,111 1.001 = [Y]дк
S- = X- + Y- 0.100 = [S]дк
То есть получаем неправильный результат как по знаку, так и в цифровой части.
Рассмотрим ещё один пример:
X = +0,101 В любом из ранее рассмотренных 0.101 = [X]дк,ок
Y = +0,111 кодов имеем 0.111 = [Y]дк,ок
S+ = X+ + Y+ 1.100 = [S]дк,ок
То есть и в этом случае происходящее переполнение в цифровой части искажает результат операции.
Можно заметить, что переполнение числовой сетки происходит в случае одинаковых знаков слагаемых, так как именно в этом случае модуль результата превосходит модули каждого из слагаемых, сам факт переполнения может быть зафиксирован изменением знака результата.
Таким образом, одним из способов фиксации переполнения является автоматическое определение перехода от одинаковых знаков слагаемых к противоположному знаку результата.
Однако такой способ фиксации переполнения неудобен, так как предварительно знаки слагаемых должны быть запомнены, сравнены между собой и после получения результата.
Существует другой принцип фиксации переполнения. Этот принцип основан на применении так называемых модифицированных кодов. Очевидно,что при переполнении разрядной сетки вычисления необходимо прекратить или, покрайней мере, выработать специальный признак переполнения, а решение о прекращении вычислений возложить на программиста.
Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется ещё один разряд:
"+" ставится в соответствие 00
"–" ставится в соответствие 11
Тогда, по определению модифицированным дополнительным кодом числа называется
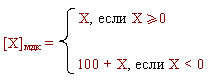 Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
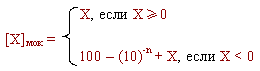 Как и в случае простого обратного кода, возникающая единица переноса в знаковых разрядах по цепи циклического переноса добавляется в младший разряд цифровой части числа.
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
S = X + Y < 2
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
S = X + Y > 1
искажает младший знаковый разряд.
Несовпадение знаковых разрядов после выполнения операции указывает на факт наличия переполнения.
При этом различают два типа переполнения:
Как и в случае простого обратного кода, возникающая единица переноса в знаковых разрядах по цепи циклического переноса добавляется в младший разряд цифровой части числа.
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
S = X + Y < 2
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
S = X + Y > 1
искажает младший знаковый разряд.
Несовпадение знаковых разрядов после выполнения операции указывает на факт наличия переполнения.
При этом различают два типа переполнения:
- "01" - положительное
- "10" - отрицательное.
Первому ставится в соответствие комбинация 01 в знаковых разрядах, а второму – 10.
Примеры
Модифицированный дополнительный код:
а) [X]мдк = 00.101 +00.101
[Y]мдк = 00.111 00.111
[S]мдк = 01.100 – положительное переполнение
б) [X]мдк = 11.101 +11.101
[Y]мдк = 11.001 11.001
[S]мдк = 1х10.110 – отрицательное переполнение
Модифицированный обратный код
а) [X]мок = 00.101 +00.101
[Y]мок = 00.111 00.111
[S]мок = 01.100 – положительное переполнение
б) [X]мок = 11.010 +11.010
[Y]мок = 11.000 11.000
1|10.010
-----  1
[S]мок = 10.011 – отрицательное переполнение 1
[S]мок = 10.011 – отрицательное переполнение
|
|



 1 (1
1 (1  i
i  Рассмотрим диапазоны представляемых чисел:
X+min = 0,000....0 - изображение положительного нуля
X+max = 0,111....1 = 1 - 2-n
X-min = 1,111....1 = -(1-2-n)
X-max = 1,000....0 - изображение отрицательного нуля.
Таким образом, нуль имеет двоякое изображение.
Замечания:
Рассмотрим диапазоны представляемых чисел:
X+min = 0,000....0 - изображение положительного нуля
X+max = 0,111....1 = 1 - 2-n
X-min = 1,111....1 = -(1-2-n)
X-max = 1,000....0 - изображение отрицательного нуля.
Таким образом, нуль имеет двоякое изображение.
Замечания:
 Если некоторое X- = -0,x1x2...xn нужно представить в дополнительном коде, то
Если некоторое X- = -0,x1x2...xn нужно представить в дополнительном коде, то
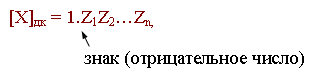 где: 1 - 0,x1x2...xn = 0, Z1Z2...Zn
Диапазоны представленных чисел:
Х+ min = 0,0...0 - положительный нуль
Х+ max = 0,11...1 = 1-2-n - максимальное положительное число.
X- min = 1,11...1 = 2-2-n - минимальное отрицательное число
X- max = 1,0...0 - наибольшее(по модулю) отрицательное число
Таким образом, нуль имеет единственное представление.
В самом деле, так как
X-X = [X+]дк + [X-]дк = 0, то в дополнительном коде: |X+| + 10 - |X-| = 10, если в разрядной сетке ЭВМ нет второго знакового разряда, то это переполнение теряется, и в знаковом разряде будет только нуль.
Важная особенность в получении дополнительного кода отрицательного числа состоит в следующем:
где: 1 - 0,x1x2...xn = 0, Z1Z2...Zn
Диапазоны представленных чисел:
Х+ min = 0,0...0 - положительный нуль
Х+ max = 0,11...1 = 1-2-n - максимальное положительное число.
X- min = 1,11...1 = 2-2-n - минимальное отрицательное число
X- max = 1,0...0 - наибольшее(по модулю) отрицательное число
Таким образом, нуль имеет единственное представление.
В самом деле, так как
X-X = [X+]дк + [X-]дк = 0, то в дополнительном коде: |X+| + 10 - |X-| = 10, если в разрядной сетке ЭВМ нет второго знакового разряда, то это переполнение теряется, и в знаковом разряде будет только нуль.
Важная особенность в получении дополнительного кода отрицательного числа состоит в следующем:
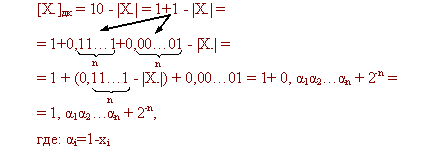 Таким образом, для записи дополнительного кода отрицательного числа необходимо в знаковом разряде поставить единицу, проинвертировать все цифровые разряды числа и прибавить единицу в младший разряд. Это также правило перевода из дополнительного кода в прямой код.
Рассмотрим на примерах выполнение операции сложения двух чисел с разными знаками.
Возможны следующие случаи:
Таким образом, для записи дополнительного кода отрицательного числа необходимо в знаковом разряде поставить единицу, проинвертировать все цифровые разряды числа и прибавить единицу в младший разряд. Это также правило перевода из дополнительного кода в прямой код.
Рассмотрим на примерах выполнение операции сложения двух чисел с разными знаками.
Возможны следующие случаи:
 То есть, нет никаких особенностей.
4. X+ = 0,105. Y- = -0,01 6. В дополнительном коде
То есть, нет никаких особенностей.
4. X+ = 0,105. Y- = -0,01 6. В дополнительном коде
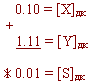 Переполнение теряется и получается верный результат.
7. X+ = 0,018. Y- = -0,11 9. В дополнительном коде
Переполнение теряется и получается верный результат.
7. X+ = 0,018. Y- = -0,11 9. В дополнительном коде
 10. X- = -0,1011. Y- = -0,01 12. В дополнительном коде
10. X- = -0,1011. Y- = -0,01 12. В дополнительном коде
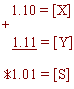 Возникающее переполнение теряется и общий результат отрицательный.
Таким образом, важной особенностью дополнительного кода является то, что знаковый разряд в процессе выполнения операции рассматривается совместно с цифровыми. Возникающие переносы теряются и не влияют на результат операции.
Возникающее переполнение теряется и общий результат отрицательный.
Таким образом, важной особенностью дополнительного кода является то, что знаковый разряд в процессе выполнения операции рассматривается совместно с цифровыми. Возникающие переносы теряются и не влияют на результат операции.

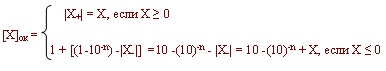






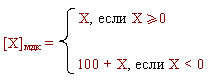 Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
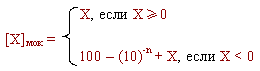 Как и в случае простого обратного кода, возникающая единица переноса в знаковых разрядах по цепи циклического переноса добавляется в младший разряд цифровой части числа.
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
S = X + Y < 2
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
S = X + Y > 1
искажает младший знаковый разряд.
Несовпадение знаковых разрядов после выполнения операции указывает на факт наличия переполнения.
При этом различают два типа переполнения:
Как и в случае простого обратного кода, возникающая единица переноса в знаковых разрядах по цепи циклического переноса добавляется в младший разряд цифровой части числа.
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
S = X + Y < 2
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
S = X + Y > 1
искажает младший знаковый разряд.
Несовпадение знаковых разрядов после выполнения операции указывает на факт наличия переполнения.
При этом различают два типа переполнения:
 1
[S]мок = 10.011 – отрицательное переполнение
1
[S]мок = 10.011 – отрицательное переполнение



