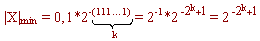Перевод чисел из одной системы счисления в другую, когда одно основание является целой степенью другого.

Как мы уже знаем, в ЭВМ наибольшее применение находит система с основаниями 2, 4, 8, 16, т.е. системы которые кратны степени 2. Поэтому целесообразно рассмотреть лишь правила перевода чисел в этих системах. Аналогичные правила будут справедливы и для других систем. Допустим, что имеется некоторое целое число N₈ в 8-ой системе. Оно может быть представлено в виде:

N₈ = a₁*8^n-1 + a₂*8^n-2 + a₃*8^n-3 +... + a_n-2*8² + a_n-1*8¹ + a_n*8⁰.

Пусть каким-либо образом мы получили запись этого числа в виде двоичного, т.е.:

N₂ = b₁*2^k-1 + b₂*2^k-2 +... + b_k-2*2² + b_k-1*2¹ + b_k*2⁰.

Разделим эти выражения на 2³ = 8:

a₁*8^n-2 + a₂*8^n-3 + a₃*8^n-4 +... + a_n-1*8⁰ + a_n*8^-1 ------- дробная часть b₁*2^k-4 + b₂*2^k-5 +... + b_k-3*2⁰ + b_k-2*2^-1 + b_k-1*2^-2 + b_k*2^-3 ------------------------- дробная часть

Так как числа были равны, то получается одинаковые частные и одинаковые остатки:

a_n*8^-1 = b_k-2*2^-1 + b_k-1*2^-2 + b_k*2^-3. (6.2)

Если снова разделим целые части на 2³ = 8, то опять получим равные частные и равные остатки.

При этом видим, что каждой восьмеричной цифре соответствует её двоичный эквивалент. Поэтому перевод выполняется простой заменой цифры восьмеричной системы её двоичным эквивалентом и обратно.

Пример:

62,753₈ = 110010,111101011₂

Аналогично для 4-ой системы:

321,2233₄ = 111001,10101111₂

Аналогично для 16-ой системы:

1D876,72 = 00011101100001110110,01110010₂

Из этих примеров видим, что чем выше основание системы счисления, тем компактнее запись.

bk-2	bk-1	bk	an

Если умножить последние соотношения (6.2) на 8, то:

a_n*8^-1*8 = (b_k-2*2^-1 + b_k-1*2^-2 + b_k*2^-3)*2³a_n = b_k-2*2² + b_k-1*2¹ + b_k*2⁰

7. Лекция: Способы представления чисел в ЭВМ
Страницы: 1 | 2 | 3 | 4 | 5 | вопросы |»	| учебники | для печати и PDA | ZIP
Если Вы заметили ошибку - сообщите нам, или выделите ее и нажмите Ctrl+Enter
В лекции представлены способы представления чисел в ЭВМ: фиксированная и плавающая запятая. Описаны прямой, дополнительный и обратный коды. Дано сложение чисел в дополнительном и обратном кодах.
Как мы уже знаем, применяются два основных способа представления чисел - с фиксированной и плавающей запятой. Большинство универсальных ЭВМ работает с числами, представленными с плавающей запятой, а большинство специализированных - с фиксированной запятой. Однако целый ряд машин работает с числами в этих двух форматах. В общем виде способ представления чисел сильно влияет на характер программирования. Так, программирование для ЭВМ, работающих в системе с фиксированной запятой, значительно усложняется, поскольку помимо алгоритмических трудностей этот процесс требует ещё отслеживания положения запятой. Фиксированная запятая Оговоримся, что разрядная сетка машины имеет постоянное число разрядов - n. При представлении чисел с фиксированной запятой считают, что запятая всегда находится перед старшим разрядом, а все числа, которые участвуют в вычислениях, считаются по абсолютной величине меньше единицы: |X| < 1 Введём две характеристики чисел: диапазон изменения и точность представления. Диапазон изменения характеризуется теми пределами, в которых могут находиться числа, с которыми оперирует машина. Отличное от нуля самое малое число: Таким образом, диапазон чисел, с которыми работает ЭВМ, есть: |X|min |X| |X|max 2^-n |X| 1 - 2^-n Иными словами, числа, которые выходят за диапазон изменения, в ЭВМ не могут быть представлены точно. Если |X| < |X|min = 2^-n, то такое число воспринимается как нуль. Если: |X| > |X|max = 1- 2^-n, то такое число воспринимается как бесконечно большое. Этим двум случаям соответствуют понятия машинного нуля и машинной бесконечности. При оптимальном округлении абсолютная ошибка: |ΔX| 0,5*2^-n Минимальная относительная ошибка: |ΔX| 0,5*2^-n | x|min = _______ = -__________ 2^-(n+1) |X|max 1-2^-n так как 1-2^-n 1 при большом "n" Максимальная относительная ошибка: |ΔX| 0,5*2^-n | X|max = _____ = _____________ = 0,5 |X|min 2^-n Ошибка представления числа зависит от величины самого числа и способа округления: 2^-(n+1) | X| 0,5 Заметим, что для малых чисел ошибка может достигать большой величины.

 

Плавающая запятая

В ЭВМ с плавающей запятой число представляется в виде:

X = ± M_x * q^±p,

где: M_x - мантисса числа;

q - основание системы счисления;

p - порядок.

Разрядная сетка машины принимает следующий вид:

Это лишь условное изображение основных слогов в числе. Заметим, что в реальной ЭВМ может быть принят любой другой порядок расположения.

Пусть "m" разрядов отведено под изображение мантиссы, а "k" разрядов под изображение порядка. Тогда для двоичной системы и нормализованного вида числа:

q = 2;

0,1 Mx < 1 - нормализованная мантисса.

То есть диапазон чисел:

Абсолютная ошибка представления числа в ЭВМ с плавающей запятой равна:

|ΔX| 0,5*2^-m

Так как

2^-1 |M_x| 1-2^-m,

то минимальная относительная ошибка:

|ΔX|_min = (0,5*2^-m) / (1 - 2^-m) 2^-(m+1), при m - большом,

а максимальная относительная ошибка:

|ΔX|_max =(0,5*2^-m) / (2^-1) = 2^-m

Видно, что относительная ошибка в ЭВМ с плавающей запятой не зависит от порядка числа. При этом точность представления больших и малых чисел изменяется незначительно.

Теоретически "плавающая запятая" имеет преимущества перед "фиксированной". Но соответствующее устройство получается намного сложнее. К тому же специфика выполнения операций с плавающей запятой требует большего числа микроопераций, что приводит к снижению быстродействия ЭВМ. Однако "плавающая запятая" снимает с программиста обязанность отслеживать положение запятой в вычислениях и значительно упрощает сам процесс программирования вычислительных задач.