
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы линейных уравнений. Матрицы и определителиСодержание книги
Поиск на нашем сайте
I. ПРОГРАММА ДИСЦИПЛИНЫ «ЛИНЕЙНАЯ АЛГЕБРА» Линейные пространства 1.1. Арифметические векторы и линейные операции над ними. Векторное пространство 1.2. Скалярное произведение векторов в Системы линейных уравнений. Матрицы и определители 2.1. Система линейных алгебраических уравнений, ее матричная запись. Решение систем линейных алгебраических уравнений методом Гаусса. 2.2. Сложение матриц и умножение матрицы на число. Ранг матрицы. Пространство решений однородной системы, связь его размерности с рангом матрицы. Теорема Кронекера-Капелли. Фундаментальная система решений однородной системы. Связь между общими решениями однородной и неоднородной систем. 2.3. Умножение матриц. Невырожденные квадратные матрицы. Обратная матрица. Нахождение обратной матрицы с помощью элементарных преобразований. Решение матричных уравнений вида 2.4. Определители и их свойства. Непосредственное вычисление определителей второго и третьего порядка. Формула разложения определителя по строкам и столбцам*. Применение определителей: 1) критерий невырожденности квадратной матрицы; 2) нахождение ранга матрицы; 3) критерий существования ненулевых решений однородной системы линейных алгебраических уравнений с Многочлены и комплексные числа 3.1. Основные понятия, связанные с многочленами. Схема Горнера и корни многочленов. Теорема Безу. НОД многочленов и алгоритм Евклида. Разложение правильной дроби на сумму элементарных дробей. 3.2. Комплексные числа и действия над ними. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Корни
4. Линейные преобразования и квадратичные формы 4.1. Линейные преобразования пространства 4.2. Билинейные и квадратичные формы, их матрицы в данном базисе. Приведение квадратичной формы к нормальному виду методом Лагранжа. Приведение квадратичной формы к каноническому виду при помощи ортогонального преобразования. Закон инерции квадратичных форм. Критерий Сильвестра знакоопределенности квадратичной формы *. Элементы аналитической геометрии 5.1. Прямая и гиперплоскость в n -мерном пространстве. Угол между гиперплоскостями. Расстояние от точки до гиперплоскости. Прямая на плоскости и в пространстве. Прямая, отрезок, луч в n -мерном пространстве. Плоскость в трехмерном пространстве. 5.2. Классификация кривых второго порядка *. Эллипс, гипербола и парабола, их свойства и канонические уравнения. Приведение общего уравнения кривой второго порядка к каноническому виду. 5.3. Классификация поверхностей второго порядка *. Эллипсоиды, параболоиды и гиперболоиды, их канонические уравнения. 5.4. Выпуклые множества в пространстве Линейное программирование 6.1. Примеры экономико-математических моделей, приводящих к задачам линейного программирования. Формы задач линейного программирования: общая, стандартная, каноническая. 6.2. Геометрическая интерпретация задачи линейного программирования в случае двух переменных. Графический метод решения. Решение задачи линейного программирования методом перебора вершин. 6.3. Метод последовательного улучшения базисного плана (симплекс-метод). Алгоритм симплекс-метода. Нахождение исходного допустимого базиса (метод искусственного базиса).
6.4. Понятие о взаимно-двойственных задачах линейного программирования. Основные теоремы двойственности. Двойственность в экономико-математических моделях.
III. СОДЕРЖАНИЕ ЗАЧЕТА И ЭКЗАМЕНА Теоретические вопросы (А) (определения, свойства и теоремы на уровне формулировок)
1. Определение линейного пространства. 2. Определение подпространства линейного пространства. Критерий подпространства. 3. Понятие линейной зависимости и линейной независимости системы векторов. Свойства линейной зависимости. 4. Определения ранга системы векторов и базиса линейного пространства. 5. Определение ортогональной системы векторов. 6. Определение скалярного произведения векторов в 7. Понятия определенной и неопределенной систем уравнений. 8. Определение фундаментального набора решений системы уравнений. 9. Определение ранга матрицы. 10. Понятия вырожденной и невырожденной матриц. 11. Определение ортогональной матрицы. 12. Правило умножения матриц. Свойства умножения матриц. 13. Определение обратной матрицы и ее свойства. 14. Свойства определителей. 15. Теоремы о целых и рациональных корнях многочленов с целыми коэффициентами. 16. Теорема Безу и следствия из нее. 17. Определение модуля и аргумента комплексного числа. 18. Формула Муавра. 19. Основная теорема алгебры. 20. Определение линейного преобразования. 21. Определения собственных векторов и собственных значений. Свойства собственных векторов. 22. Определение квадратичной формы. 23. Закон инерции квадратичных форм. 24. Критерий Сильвестра. 25. Формула расстояния между точками в многомерном пространстве. Свойства расстояния. 26. Определение отрезка, теорема об отрезке. 27. Определение 28. Определение и свойства выпуклого множества. 29. Определение и примеры кривых второго порядка. 30. Определение и примеры поверхностей второго порядка. 31. Определение угловых точек выпуклого множества. 32. Определение стандартной задачи линейного программирования. 33. Определение канонической задачи линейного программирования. 34. Графическое решение задач линейного программирования. 35. Определение двойственной задачи линейного программирования. 36. Симплекс-метод решения задач линейного программирования.
Теоретические вопросы (Б) (теоретические вопросы на доказательство)
1. Неравенство Коши-Буняковского. 2. Неравенство треугольника. 3. Линейная независимость лестничной системы векторов. 4. Однозначность разложения вектора по базису. 5. Формула умножения комплексных чисел в тригонометрической форме. 6. Формула деления комплексных чисел в тригонометрической форме. 7. Существование бесконечного числа решений у системы линейных однородных уравнений, в которой число неизвестных больше числа уравнений. 8. Теорема о пространстве решений однородной системы линейных алгебраических уравнений. 9. Теорема о связи общих решений неоднородной и однородной систем линейных алгебраических уравнений. 10. Формулы Крамера для системы двух линейных уравнений с двумя переменными. 11. Линейная независимость векторов, составляющих ортонормированную систему. 12. Формулы для вычисления координат вектора в ортогональном базисе. 13. Невырожденность ортогональной матрицы.
14. Изменение матрицы линейного преобразования при замене базиса. 15. Равенство характеристических многочленов подобных матриц. 16. Ортогональность собственных векторов, соответствующих различным собственным значениям самосопряженного линейного преобразования. 17. Изменение матрицы квадратичной формы при замене базиса. 18. Вывод канонического уравнения эллипса. 19. Вывод канонического уравнения гиперболы. 20. Выпуклость пересечения выпуклых множеств. 21. Переход от стандартной задачи линейного программирования к канонической. 22. Переход от канонической задачи линейного программирования к стандартной. 23. Линии уровня и графическое решение задач линейного программирования. 24. Алгоритм симплекс-метода. 25. Нахождение исходного допустимого базиса (метод искусственного базиса). 26. Основные теоремы двойственности.
Практические задания
Примеры задач (А) 1. Найдите вектор 2. Найдите вектор 3. Найдите длину вектора 4. Найдите скалярное произведение векторов 5. Найдите косинус угла между векторами 6. Вычислите: 7. Вычислите ранг системы векторов: а) 8. Разложите вектор 9. Исследуйте на линейную зависимость систему векторов: а) 10. Найти координаты вектора 11. Решите по формулам Крамера систему уравнений: а) 12. Решите методом Гаусса систему уравнений 13. Решите систему уравнений 14. Найдите фундаментальный набор решений системы 15. Найдите размерность пространства решений однородной системы линейных уравнений, записанной в матричной форме: а) 16. Решите систему линейных уравнений, заданную в матричной форме:
17. Решите систему линейных уравнений: 18. Найдите ранг матрицы: а) г) 19. Найдите матрицу 20. Найдите матрицу 21. Вычислите а) в) 22. Вычислите 23. Вычислите матрицу 24. Вычислите 25. Вычислите определитель матрицы 26. Вычислите: а) 27. Вычислите определитель матрицы 28. Вычислите определитель матрицы 29. Найдите целые корни многочленов а) 30. Найдите наибольший общий делитель многочленов: а) б) 31. Запишите в тригонометрической форме комплексное число 32. Решите уравнение в области комплексных чисел: а)
б) 33. Найдите модуль комплексного числа 34. Найдите модуль комплексного числа
35. Найдите аргумент комплексного числа а) б) в) 36. Запишите квадратное уравнение с действительными коэффициентами, которое имеет корень 37. Найдите собственные значения матрицы: а) г) 38. Найдите собственные значения матрицы 39. Найдите собственные значения матрицы 40. В пространстве столбцов 41. В пространстве 42. В пространстве столбцов 43. В пространстве 44. Линейное преобразование 45. Вычислите ранг квадратичной формы: а) б) в) г) 46. Вычислите ранг квадратичной формы, если ее матрица в некотором базисе имеет вид: а) 47. Выясните, является ли положительно определенной квадратичная форма 48. Выясните, является ли знакоопределенной квадратичная форма
49. Найдите угол а) 50. Найдите точку пересечения прямых 51. Записать общее уравнение прямой на плоскости, которая проходит через точку 52. Записать общее уравнение прямой на плоскости, которая проходит через точку 53. Найдите уравнение прямой, содержащей точку 54. Найдите общее уравнение прямой, проходящей через точки 55. Найдите общее уравнение прямой, содержащей точку 56. Найдите расстояние от точки а) 57. Найдите эксцентриситет эллипса 58. Найдите эксцентриситет гиперболы 59. Запишите уравнения асимптот гиперболы 60. Определите вид кривой второго порядка, заданной уравнением: а) в) 61. Две прямые заданы уравнениями 62. Найдите косинус угла между плоскостями 63. Найдите расстояние от точки 64. Найдите расстояние между параллельными плоскостями 65. Найдите общее уравнение плоскости, проходящей через точку 66. Найдите общее уравнение плоскости, содержащей точку 67. Найдите общее уравнение плоскости 68. Найдите общее уравнение плоскости, проходящей через три точки а) 69. Найдите точку пересечения прямой 70. Найдите длину отрезка 71. Пусть 72. Пусть 73. Решите графически задачи линейного программирования:
74. Привести к стандартной форме следующую задачу линейного программирования:
75. Дана начальная симплекс-таблица задачи линейного программирования на минимум:
Решить задачу симплекс-методом.
Примеры задач (Б) 1. Разложите векторы 2. При каких значениях параметра 3. Даны векторы 4. Найти все значения параметра 5. При каких значениях параметра 6. При каких значениях параметра 7. При каких значениях параметра 8. При каких значениях параметра 9. Найдите значения параметра а) 10. Найдите общее решение системы линейных уравнений, заданной в матричной форме: а) в) 11. Найдите значения параметра 12. При каких значениях параметра 13. При каких значениях параметра 14. При каких значениях параметра 15. При каких значениях параметра 16. При каких значениях параметра 17. Используя равенство 18. Вычислите степень ортогональной матрицы 19. Вычислите определитель матрицы а) в) 20. Найдите определитель матрицы 21. Представьте дробь в виде суммы многочлена и простейших дробей над а) б) 22. Решите систему уравнений по формулам Крамера: 23. Методом Лагранжа приведите к нормальному виду квадратичную ф
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.70.108 (0.009 с.) |

 . Геометрический смысл пространств
. Геометрический смысл пространств  и
и  . Линейные пространства общего вида. Линейная зависимость системы векторов и ее геометрический смысл. Базис и размерность линейного пространства. Координаты вектора в данном базисе. Преобразование координат векторов при замене базиса. Подпространства линейного пространства.
. Линейные пространства общего вида. Линейная зависимость системы векторов и ее геометрический смысл. Базис и размерность линейного пространства. Координаты вектора в данном базисе. Преобразование координат векторов при замене базиса. Подпространства линейного пространства. .
. неизвестными, состоящей из
неизвестными, состоящей из  и его свойства.
и его свойства. - плоскости. Гиперплоскость.
- плоскости. Гиперплоскость. .
. .
. , где
, где  ,
,  и
и  .
. из уравнения
из уравнения  , если
, если  ,
,  и
и  .
. , где
, где  и
и  .
. и
и  .
. и
и  .
. , где
, где  ,
,  ,
,  .
.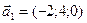 ,
,  ,
,  ; б)
; б)  ,
,  ,
,  .
. по базису
по базису  ,
,  .
. ,
,  ,
,  ; б)
; б)  ,
,  ,
,  .
. в ортогональном базисе:
в ортогональном базисе:  ,
,  .
. ; б)
; б)  ; в)
; в)  .
. , выбирая
, выбирая  и
и  в качестве базисных переменных. В ответе укажите базисное решение.
в качестве базисных переменных. В ответе укажите базисное решение. , выбирая
, выбирая  и
и  в качестве базисных переменных. В ответе укажите базисное решение.
в качестве базисных переменных. В ответе укажите базисное решение. .
. ; б)
; б)  ;
; .
.
 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ;е)
;е)  .
. , если
, если  и
и  .
. , если
, если  , где
, где  ,
,  .
. где:
где: и
и  ; б)
; б)  и
и  ;
; и
и  ; г)
; г)  и
и  ;
; где
где  и
и  .
. .
. , если: а)
, если: а) 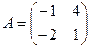 ; б)
; б)  .
. .
. ; б)
; б)  .
. , если
, если  .
. .
. ; б)
; б)  .
. и
и 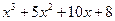 ;
; и
и 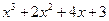 .
. .
. ;
; .
. , если
, если  .
. , если:
, если: а)
а)  ,
,  ,
,  ; б)
; б)  ,
,  ,
,  , если:
, если: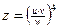 ,
,  ,
,  ,
,  ;
; ,
,  ,
,  ;
; ,
,  ,
,  .
. .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
. , если
, если  .
. , если
, если  .
.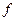 по правилу:
по правилу:  . Напишите матрицу
. Напишите матрицу  преобразования
преобразования  , где
, где  .
. действует линейное преобразование
действует линейное преобразование  . Напишите матрицу преобразования
. Напишите матрицу преобразования  действует линейное преобразование
действует линейное преобразование  . Найдите образ вектора
. Найдите образ вектора  .
. действует линейное преобразование
действует линейное преобразование  . Найдите образ вектора
. Найдите образ вектора  .
. . Найдите образ
. Найдите образ  вектора
вектора  .
. ;
; ;
;
 .
.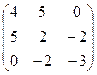 ; б)
; б)  ; в)
; в) 
 .
. .
. с вершинами
с вершинами ,
,  ,
,  ; б)
; б) 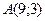 ,
,  ,
,  ; в)
; в)  ,
,  ,
,  ; г)
; г)  ,
,  ,
,  .
.
 и
и  .
. , в направлении вектора
, в направлении вектора  .
. имеет нормальный вектор
имеет нормальный вектор  .
. и перпендикулярной к прямой, проходящей через точки
и перпендикулярной к прямой, проходящей через точки  и
и  .
. и
и  .
. и параллельной прямой
и параллельной прямой  .
.
 ,
,  ;б)
;б)  ,
,  .
. .
. .
. .
. ; б)
; б)  ;
; .
. и
и  . Найдите косинус угла между ними.
. Найдите косинус угла между ними. и
и  .
. до плоскости
до плоскости  .
. и
и 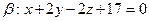 .
. и перпендикулярной прямой
и перпендикулярной прямой  .
. и перпендикулярной вектору
и перпендикулярной вектору  .
. , которая параллельна плоскости
, которая параллельна плоскости  и проходит через точку
и проходит через точку 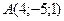 .
. ,
,  ,
,  ; б)
; б)  ,
,  ,
,  ; в)
; в)  ,
,  ,
,  .
. и плоскости
и плоскости  .
. , если
, если  ,
,  .
. – выпуклая оболочка точек
– выпуклая оболочка точек  ,
,  ,
,  . Найдите ограничения в виде системы неравенств, которые задают множество
. Найдите ограничения в виде системы неравенств, которые задают множество  ,
,  ,
,  ,
,  . Найдите ограничения в виде системы неравенств, которые задают множество
. Найдите ограничения в виде системы неравенств, которые задают множество  ,
,  ,
,
 .
. .
. и
и  по базису, состоящему из векторов
по базису, состоящему из векторов  ,
,  ,
,  .
.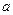 векторы
векторы  ,
,  ,
,  линейно зависимы? Выразить вектор
линейно зависимы? Выразить вектор 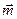 в виде линейной комбинации векторов
в виде линейной комбинации векторов  и
и  .
. ,
,  ,
,  ,
,  . При каких значениях параметров
. При каких значениях параметров  ,
,  верно равенство
верно равенство  ?
? , при которых вектор
, при которых вектор  линейно выражается через векторы
линейно выражается через векторы  ,
,  ,
,  .
.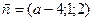 и
и  ортогональны?
ортогональны? ,
,  ,
,  ?
? ,
,  ,
,  образуют ортогональный базис пространства
образуют ортогональный базис пространства  векторы
векторы  ,
,  ,
,  компланарны?
компланарны? линейно зависимы:
линейно зависимы: ; б)
; б)  .
. ; б)
; б)  ;
; .
. .
. имеет ненулевые решения?
имеет ненулевые решения? имеет единственное решение?
имеет единственное решение? является невырожденной?
является невырожденной? равен 4?
равен 4? равен 3?
равен 3? , найдите матрицу
, найдите матрицу  .
. .
. ; б)
; б)  ;
; .
. .
. :
: ;
; .
. .
.


