
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV. Образцы билетов к зачету (1-ый семестр)Содержание книги
Поиск на нашем сайте
Вариант 1 1. Дайте определение квадратной матрицы. Приведите пример квадратной матрицы третьего порядка ранга 2. Чему равен ее определитель? 2. Докажите, что для ненулевых векторов 3. Найти координаты вектора 4. Вычислить произведения матриц: 5. Вычислить обратную матрицу для следующей матрицы Вариант 2 1. Сформулируйте правило Крамера для решения систем линейных алгебраических уравнений. Приведите пример применения правила Крамера. 2. Опишите операцию сопряжения комплексных чисел. Покажите, что сопряжение сохраняет сумму и произведение комплексных чисел. 3. Из системы столбцов заданной матрицы A выделить максимальную линейно независимую подсистему и представить остальные столбцы в виде линейных комбинаций выделенных:
4. Вычислить определитель матрицы
5. Решить матричное уравнение
V. ОБРАЗЦЫ ЭКЗАМЕНАЦИОННЫХ БИЛЕТОВ (2-ой семестр) Вариант 1 1. Дайте определение ранга матрицы. Приведите примеры матриц третьего порядка рангов 1, 2 и 3. Что можно сказать об определителе произвольной матрицы размера 2. Приведите пример симплекс-таблицы задачи линейного программирования, имеющей единственное решение. 3. Дайте определение фундаментального набора решений однородной системы линейных уравнений. Из скольких элементов он состоит? Приведите пример. Ответ обосновать. 4. Дополнить следующие векторы до ортогонального базиса: 5. Вычислить матрицу 6. Вычислить определитель матрицы
7. Найти канонические уравнения сторон треугольника ABC с вершинами 8. Найти решение следующей задачи линейного программирования:
Вариант 2 1. Дайте определение произведения матриц A и B. Приведите пример. Для любых ли квадратных матриц верно равенство 2. Приведите пример симплекс-таблицы задачи линейного программирования, не имеющей решения. 3. Запишите общее решение однородной системы линейных уравнений. Образует ли множество решений однородной системы линейных уравнений линейное пространство? Ответ обосновать. 4. Найти общее решение следующей системы линейных уравнений, заданной в матричной форме:
5. Найти матрицу 6. Вычислить определитель матрицы 7. Найти уравнения сторон треугольника с вершинами 8. Привести к стандартной форме следующую задачу линейного программирования:
VI. ОТВЕТЫ Примеры задач (А) 1. max в точке: Примеры задач (Б) 1. Образцы билетов для зачета (1-й семестр) Вариант 1 2. 5.. Вариант 2
3. Ранг матрицы A равен 2. Ответ. 5. Образцы экзаменационных билетов (2-й семестр) Вариант 1 4. Ответ. Вариант 2 4. Частное решение: 5. 6. -4. 7. 8.
VII. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
* Без доказательства (здесь и далее по тексту).
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.52.111 (0.007 с.) |

 выполняются неравенства
выполняются неравенства 
 в ортогональном базисе:
в ортогональном базисе:  ,
,  ,
, 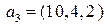 .
. и
и 
 .
. .
. .
. .
. .
. ранга n? Ответ обосновать.
ранга n? Ответ обосновать. ,
,  .
. .
. .
. ,
,  ,
,  .
.
 ? Ответ обосновать.
? Ответ обосновать. .
. .
. .
.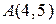 ,
,  ,
,  .
.
 ; 2.
; 2.  ; 3. 8; 4.
; 3. 8; 4.  ; 5.
; 5.  ; 6.
; 6.  ; 7. а) 3; б) 2; 8.
; 7. а) 3; б) 2; 8.  ; 9. а) линейно зависима; б) линейно независима; 10.
; 9. а) линейно зависима; б) линейно независима; 10.  ,
,  ; 11. а)
; 11. а)  ,
,  ; б)
; б)  ,
,  ; в)
; в)  ; 12.
; 12. 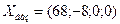 ; 13.
; 13.  ; 14.
; 14.  ,
,  ; 15. а) 3; б) 1; 16.
; 15. а) 3; б) 1; 16.  ,
,  ,
,  ; 17.
; 17.  ,
,  ,
,  ; 18. а) 3; б) 4; в) 2; г) 2; д) 2; е) 3; 19.
; 18. а) 3; б) 4; в) 2; г) 2; д) 2; е) 3; 19.  ; 20.
; 20.  ; 21. а)
; 21. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; 22.
; 22.  ; 23.
; 23.  ; 24. а)
; 24. а)  ; б)
; б)  ; 25. 36; 26. а) 54; б) 48; 27. 64; 28.
; 25. 36; 26. а) 54; б) 48; 27. 64; 28.  ; 29. а) 2,
; 29. а) 2,  ; б)
; б)  , 1; 30. а)
, 1; 30. а)  ; б)
; б) 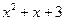 ; 31.
; 31. 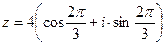 ; 32.
; 32.  ; 33.
; 33.  ; 34. а) 10; б)
; 34. а) 10; б)  ; 35. а)
; 35. а)  ; б)
; б)  ; в)
; в)  ; 36.
; 36.  ; 37. а)
; 37. а)  ,
, 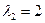 ; б)
; б)  ,
,  ; в)
; в)  ,
,  ; г)
; г) 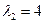 ,
,  ; д)
; д)  ,
,  ; е)
; е)  ,
,  ,
,  ; 38.
; 38.  ,
, 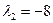 ; 39.
; 39.  ,
,  ; 40.
; 40.  ,
,  ; 41.
; 41.  ; 42.
; 42.  ; 43.
; 43.  ; 44.
; 44. 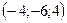 ; 45. а) 3; б) 2; в) 1; г) 1; 46. а) 3; б) 1; в) 2; 47. Да; 48. Нет; 49. а) 60°; б) 45°; в) 30°; г) 90°; 50.
; 45. а) 3; б) 2; в) 1; г) 1; 46. а) 3; б) 1; в) 2; 47. Да; 48. Нет; 49. а) 60°; б) 45°; в) 30°; г) 90°; 50. 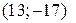 ; 51.
; 51.  ; 52.
; 52.  ; 53.
; 53.  ; 54.
; 54.  ; 55.
; 55.  ; 56. а) 2; б) 2; 57.
; 56. а) 2; б) 2; 57.  ; 58.
; 58.  ; 59.
; 59.  ; 60. а) Гипербола; б) Эллипс; в) Парабола; 61.
; 60. а) Гипербола; б) Эллипс; в) Парабола; 61.  ; 62.
; 62.  ; 63. 7; 64. 3; 65.
; 63. 7; 64. 3; 65.  ; 66.
; 66.  ; 67.
; 67.  ; 68.
; 68.  ; 69.
; 69.  ; 70. 5; 71.
; 70. 5; 71.  ; 72.
; 72.  ; 73. a) min в точке
; 73. a) min в точке  б) min в точке:
б) min в точке:  ,
, , в) max в точке:
, в) max в точке:  74.
74.  75.
75. 
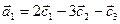 ,
,  ; 2.
; 2.  ,
,  ; 3.
; 3.  ,
,  ,
, 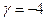 ; 4.
; 4.  ; 5.
; 5.  ,
,  ; 6.
; 6. 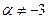 ; 7.
; 7.  ; 8.
; 8.  ; 9. а)
; 9. а)  ; б)
; б)  ; 10. а)
; 10. а) 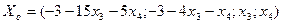 ; б)
; б)  ; в)
; в)  ; 11.
; 11.  ; 12.
; 12.  ,
,  ; 13.
; 13.  ,
,  ; 14.
; 14.  ,
,  ; 15.
; 15. 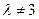 ,
, 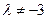 ; 16.
; 16.  ,
,  ,
,  ,
,  ; 17.
; 17.  ; 18.
; 18.  ; 19. а) 8; б) 72; в)
; 19. а) 8; б) 72; в)  ; 20.
; 20.  ; 21. а)
; 21. а)  ; б)
; б)  22. (1; 4); 23.
22. (1; 4); 23.  ; 24.
; 24.  ; 25.
; 25.  ; 26. а)
; 26. а)  ; б)
; б)  ; 27. а)
; 27. а)  ; б)
; б)  ; 28.
; 28.  ,
,  ; б)
; б) 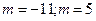 ; в)
; в)  ; 30.
; 30.  ; 31.
; 31.  ; 32.
; 32.  ,
,  ,
,  ; 33.
; 33.  ; 34.
; 34. 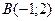 ; 35.
; 35.  ; 36.
; 36.  ; 37. 12; 38.
; 37. 12; 38.  ; 39.
; 39.  ; 40.
; 40.  ; 41.
; 41.  ; 42.
; 42.  ; 43.
; 43.  ; 44.
; 44.  ; 45.
; 45. 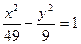 ; 46.
; 46.  ; 47.
; 47.  ; 48.
; 48. 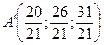 ; 49.
; 49.  ; 50.
; 50.  ; 51.
; 51.  ; 52.
; 52.  ; 53.
; 53.  ,
,  ,
,  ; 54.
; 54.  ; 55.
; 55.  ; 57. а) (3; 3), (12; 7), (7; 13); б) (2;4;0;60;0), (11;8;60;0;0), (5;12;0;0;60); 58. а) max в точке
; 57. а) (3; 3), (12; 7), (7; 13); б) (2;4;0;60;0), (11;8;60;0;0), (5;12;0;0;60); 58. а) max в точке 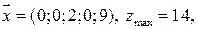 б) max в точке
б) max в точке  min в точке
min в точке  59.
59. 
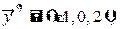
 .
.
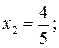
 ; 4.
; 4. 
 .
. .
. . 4. 114;
. 4. 114; .
. ; 5.
; 5. 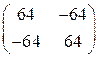 . 6. 48; 7.
. 6. 48; 7.  ,
,  ,
, 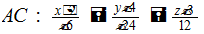 ; 8. Оптимальное решение
; 8. Оптимальное решение  достигается при
достигается при 
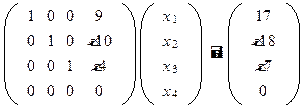 . Ранг системы равен 3.
. Ранг системы равен 3.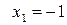 ,
,  ,
,  ,
,  .
.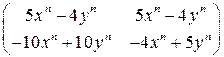 .
. :
:  ,
,  :
:  ,
,  :
:  .
. .
.


