

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Минимальные конъюнктивные нормальные формы
Как было отмечено, для получения минимальной формы функции нужно построить как МДНФ так и МКНФ.
Рассмотрим построение МКНФ.
В основном методы получения МКНФ аналогичны методам получения МДНФ и поэтому сформулируем лишь правила получения МКНФ:
- Представить ФАЛ в СКНФ. Если она задана таблицей, то произвести запись функции по нулям, как это было сформулировано ранее. Если дана СДНФ, то из нее легко получить СКНФ:
f(x1x2x3) = x1x2x3  x1x2x3 x1x2x3  x1x2x3 x1x2x3  x1x2x3 x1x2x3  x1x2x3 = (x1 x1x2x3 = (x1  x2 x2  x3) (x1 x3) (x1  x2 x2  x3) (x1 x3) (x1  x2 x2  x3), x3),
т.е. нужно функцию представить в виде конъюнкции недостающего числа дизъюктивных членов с соответсвенно расставлеными отрицаниями.
- При задании функции в произвольной конъюктивной форме, применяя
формулы развертывания:
x = (x  y)(x y)(x  y) = xx y) = xx  xy xy  yx yx  yy (x yy (x  y) = (x y) = (x  y y  z)(x z)(x  y y  z) z)
............,
получить СКНФ.
- Выполнить все операции неполного склеивания:
(x  y)(x y)(x  y) = x(x y) = x(x  y)(x y)(x  y) y)
и поглощения: x(x  y) = x, получить сокращенную КНФ. y) = x, получить сокращенную КНФ.
- Применить любой из методов минимизации: испытание членов, диаграммы Вейча, метод импликантных матриц.
- При выполнении метода испытания членов необходимо каждый конъюктивный член приравнять нулю. Найти значения аргументов, которые обращают его в нуль, удалить его из выражения функции и найти значение функции при найденных значениях аргументов. Если функция обратится в нуль, то конъюктивный член является лишним.
По возможности отбросить одновременно несколько членов, поступить как и при минимизации функции ДНФ.
- При использовании диаграмм Вейча ищутся правильные конфигурации, образованные нулями.
- При применении метода импликантных матриц поступают как и в случае ДНФ, только колонкам присваивают имена конституент "0" функции, записанной в СКНФ, а горизонтальным рядам – простых импликант. Далее ищут оптимальное покрытие.
| 6. Лекция: Арифметические основы
| 
| 
| 
| | Страницы: 1 | 2 | 3 | 4 | вопросы |»
| | учебники | для печати и PDA | ZIP
| 
| | Если Вы заметили ошибку - сообщите нам, или выделите ее и нажмите Ctrl+Enter
| 
| | В лекции описаны системы счисления, представлена методика выбора системы счисления, даны правила перевода чисел из одной системы счисления в другую.
| 
| 
| 
| В данном разделе курса рассматриваются способы представления чисел в ЭВМ, методы выполнения арифметических операций, которые отличны от методов, получивших широкое распространение на практике.
Как известно, еще в 19 веке производство операций над числами, содержащими много разрядов, представлялось сложной задачей, решить которую могли только профессионалы. Именно в это время были разработаны основные правила выполнения операций над многозначными числами узбекским математиком Аль-Хорезми. Общие закономерности, по которым строились эти правила, впоследствии получили название АЛГОРИТМА. Они настолько широко вошли в жизнь, что, производя эти операции над многозначными числами, мы не задумываемся над тем, что выполняем строгую систему правил.
Система счисления.
Способ представления изображения произвольных чисел с помощью некоторого конечного множества символов назовем системой счисления.
В повседневной практике мы пользуемся, как правило, десятичной системой счисления. Ответ на вопрос: " Почему именно эта система счета получила наибольшее распространение? " - сейчас дать затруднительно. В литературе, как правило, в качестве обоснования приводится тот факт, что на руках человека - в сумме 10 пальцев. Вряд ли это обоснование можно принимать всерьез. На практике мы сталкиваемся и с более сложными, в частности, со смешанными системами. Например, система счета времени, где за единицу принята секунда, минута, час, сутки, неделя, месяц, год. Или система счета денег, до недавнего времени применявшаяся в Англии (пенс, шиллинг, фунт):
12п = 1ш, 20ш = 1ф.
Или еще более интересная - римская система счета, которая исользует символы: I - 1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000.
Эта система является особой и применяется редко (циферблат, архитектура, история и т.д.)
Системы счисления принято делить на:
- Позиционные.
- Непозиционные.
- Символические.
Начнем с последних. В этих системах каждому числу ставится в соответствие свой символ. Эти системы не находят широкого применения в силу естественной их ограниченности (алхимия, кодированные сообщения) -бесчисленного множества символов, которое требуется для изображения всех возможных чисел. Поэтому эти системы из рассмотрения опустим.
Позиционные системы счисления.
Само название этих систем указывает на связь значимости числа и его изображения от позиции.
Позиция - некоторое место, в котором может быть представлен лишь один символ.
Примером позиционной системы счисления является десятичная система.
В этой системе число представляется в виде полинома "n" степени, а изображается совокупностью некоторых символов, каждый из которых имеет различный вес в зависимости от позиции, которую он занимает.
a4a3a2a1 - число; a1, a2, a3, a4 - символы.
Всем позициям приписывается различный вес, который чаще всего выбирается как целая степень основания системы.
Основание системы счисления - число, которое является мощностью множества различных символов, допустимых в каждой позиции числа.
Так для десятичной системы допускаемыми являются символы: 0, 1, 2, 3,..., 9.
Обозначим через "p" основание системы счисления. Тогда веса позиций числа могут быть представлены так:
... p3 p2 p1 p0.
Само число, изображение которого имеет вид, например, a4a3a2a1 может быть представлено так:
a0p0 + a1p1 + a2p2 + a3p3 - это развернутая запись числа в позиционной системе.
Например:
97310 = 3*100 + 7*101 + 9*102 = 3 + 70 + 900.
В отличие от системы счета времени, десятичная система является однородной, т.е. одних и тех же десятичных символов достаточно, чтобы изобразить любое число. В то время как в смешанных системах нужно придумывать все новые и новые символы для того, чтобы изобразить следующее по величине число.
Таким образом, однородность - одно из важных свойств позиционных систем.
Любое число X в позиционной системе счисления можно представить в виде:
n
X = ±pm Σ aip-i,
i=1
где
m - число позиций или разрядов, отведенное для изображения целой части числа.
n - общее число разрядов в числе.
ai - любой допустимый символ в разряде, т.е. ai = {0, 1, 2,..., p-1}.
p - основание системы счисления.
Например:
- 961,13 = - (9*102 + 6*101 + 1*100 + 1*10-1 + 3*10-2).
- Заметим, что число, равное основанию системы счисления, т.е. "p", в самой системе с основанием "p" записывается только в двух позициях (разрядах), а именно так:
pp = 10p
- Заметим также, что разделение числа на две части - дробную и целую - имеет смысл лишь в позиционных системах.
- Заметим, что основание системы для представления числа мы можем выбрать произвольное. Такой же произвол мы можем допустить и в назначении весов разрядов. Однако наиболее целесообразно считать его, как и в десятичной системе, естественным, т.е. ввести в качестве степеней основания числа натурального ряда:
4.... +3, +2, +1, 0, -1, -2, -3...
|
Выбор системы счисления.
Возникает естественный вопрос, является ли общепринятая система счисления с основанием 10 оптимальной? Если да, то с каких позиций? Вопрос заслуживает внимания, т.к. одна из первых ВМ (ENIAC) использовала именно десятеричную систему.
Прямой и однозначный ответ на этот вопрос невозможен. Можно дать много различных ответов и все они будут справедливы лишь для каких-то определенных условий.
Введя общее представление числа в позиционной системе, мы усомнились в достоинствах десятеричной не потому, что она вдруг проявила свои отрицательные качества, а потому что ее преимущества явны лишь при ручных методах счета. Нас же интересуют, прежде всего, такие системы счисления, которые будут удобны и экономичны при автоматических вычислениях с помощью ЭВМ. Мы должны также помнить, что необходимо для этого иметь саму ЭВМ.
Покажем, что десятеричная система не устарела. Например, для производства экономичных расчетов обычно приходится иметь дело с очень большими объемами числовой информации. Тогда с введением новой системы пришлось бы воспользоваться следующей цепочкой действий:
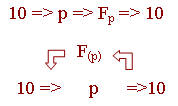 Т.е. нужно было бы из десятеричной системы перевести информацию в "p"-систему, произвести над ней необходимые операции в системе "p", затем снова сделать, но обратный перевод из "p"-системы в десятеричную, т.к. отказ от десятеричной системы потребовал бы и устранения первого этапа.
Если преобразование из десятеричной системы в "p"-систему требует не слишком много времени, в то же время, если выполнение функции F будет в системе "p" сделано много быстрее, то тогда эта цепочка действий будет оправданной.
Но для экономической информации характерно то, что очень несложные операции нужно производить всякий раз над большим объемом исходных данных. Так что в данном случае вряд ли целесообразно переходить к новой системе. Это и является объяснением того факта, что в настоящее время значительное число ЭВМ строится именно в десятеричной системе счисления.
Однако ЭВМ предназначены не только для выполнения экономических расчетов. В большинстве случаев неэкономических применений ЭВМ имеют дело с задачами, в которых общий объем исходных данных невелик, но общее число необходимых операций огромно. Именно для такого рода применений рассмотренная последовательность действий может оказаться выгодной.
Очевидно, что можно, не сужая области применения ЭВМ, задаться величиной некоторого самого большого числа. Пусть это будет число M. Воспользуемся позиционной системой счисления с основанием "p", и тогда потребуется "n" разрядов, чтобы представить все M чисел:
M = pn - 1 (от 0 до pn - 1)
M ≈ pn
logpM = n*logpp, где logpp = 1, тогда n = logpM.
Оборудование, которое нужно для хранения любого числа от 0 до M пропорционально произведению основания системы счисления на количество разрядов.
Таким образом, при заданном числе M количество цифроразрядов при основании "p":
p*n = p* logpM, (6.1)
где:
цифроразряд - эквивалент оборудования,
p*n - число устойчивых состояний элемента памяти,
n - число разрядов в числе.
Рассмотрим пример:
Пусть есть 24 цифроразряда.
Т.е. нужно было бы из десятеричной системы перевести информацию в "p"-систему, произвести над ней необходимые операции в системе "p", затем снова сделать, но обратный перевод из "p"-системы в десятеричную, т.к. отказ от десятеричной системы потребовал бы и устранения первого этапа.
Если преобразование из десятеричной системы в "p"-систему требует не слишком много времени, в то же время, если выполнение функции F будет в системе "p" сделано много быстрее, то тогда эта цепочка действий будет оправданной.
Но для экономической информации характерно то, что очень несложные операции нужно производить всякий раз над большим объемом исходных данных. Так что в данном случае вряд ли целесообразно переходить к новой системе. Это и является объяснением того факта, что в настоящее время значительное число ЭВМ строится именно в десятеричной системе счисления.
Однако ЭВМ предназначены не только для выполнения экономических расчетов. В большинстве случаев неэкономических применений ЭВМ имеют дело с задачами, в которых общий объем исходных данных невелик, но общее число необходимых операций огромно. Именно для такого рода применений рассмотренная последовательность действий может оказаться выгодной.
Очевидно, что можно, не сужая области применения ЭВМ, задаться величиной некоторого самого большого числа. Пусть это будет число M. Воспользуемся позиционной системой счисления с основанием "p", и тогда потребуется "n" разрядов, чтобы представить все M чисел:
M = pn - 1 (от 0 до pn - 1)
M ≈ pn
logpM = n*logpp, где logpp = 1, тогда n = logpM.
Оборудование, которое нужно для хранения любого числа от 0 до M пропорционально произведению основания системы счисления на количество разрядов.
Таким образом, при заданном числе M количество цифроразрядов при основании "p":
p*n = p* logpM, (6.1)
где:
цифроразряд - эквивалент оборудования,
p*n - число устойчивых состояний элемента памяти,
n - число разрядов в числе.
Рассмотрим пример:
Пусть есть 24 цифроразряда.
| Основание p.
| Возможное число цифроразрядов.
| Наибольшее число M.
| |
| 2*12
| 1*1*...*12 = 409510
\________/
| |
| 3*8
| 2*2*...*23 = 656010
\________/
| |
| 4*6
| 3*3*...*34 = 409510
\________/
| |
| 6*4
| 5*5*5*56 = 129510
\______/
| |
| 8*3
| 7*7*78 = 51110
\____/
| Количество цифроразрядов говорит как о величине оборудования, так является характеристикой быстродействия. Как увидим позже, в позиционной системе счисления времена выполнения операций могут быть выражены через количество разрядов в числе.
Считаем "p" - величиной непрерывной. Находим производную от (6.1) по величине "p". Берем вторую производную по "p". Увидим, что первая производная обращается в нуль, а вторая - больше нуля при p = e. Т.е. получаем минимум при p = e.
Таким образом, оптимальной по оборудованию и быстродействию является система с основанием е.
Но е = 2,718...
Поэтому оптимальной является система с основанием р = 3.
Построим функцию, характеризующую отношение оборудования в системе с основанием "p" относительно системы с основанием "2".
| p
|
|
|
|
|
|
|
|
|
| | f(p)
| 1,000
| 0,946
| 1,000
| 1,078
| 1,148
| 1,247
| 1,333
| 1,420
| 1,595
| Т.е. 10-я система является более чем в 1,5 раза неэкономичной по отношению ко 2-ой системе, а 3-я система оказывается лишь на 5% экономичнее 2 й.
Действительное обоснование экономичности той или иной системы выглядит несколько сложнее.
Когда говорим об экономичности, то, прежде всего, имеем ввиду объем оборудования, сосредоточенный в АУ и ЗУ. Объем оборудования УУ не находится в столь простой зависимости от "p" да и в АУ учитывается лишь оборудование, связанное с элементами хранения информации, но не логическое оборудование.
Более детальный анализ показывает, что наиболее эффективными являются системы с основанием, кратным 2, т.е. 2, 4, 8, 16. Специфика построения схем ЭВМ показывает, что наиболее эффективной является 16-ая система. Именно она и применяется в современных машинах.
Мы же будем считать эффективной систему с основанием 2 по причине ее наибольшего распространения.
Вот основные соображения в пользу этой системы:
- Высокая информационная эффективность.
- Простота и надежность работы 2-ого элемента хранения информации (т.е. имеющего 2 устойчивых состояния)
- Совпадение максимального числа состояний элемента с максимальным числом значений двоичной переменной, дающее возможность не строить специальные устройства для выполнения логических операций.
- Простота построения схем для выполнения простых операций.
- Более высокая скорость выполнения основных арифметических операций.
Последнее требует специального пояснения. В данном случае рассматриваются не отрезки времени, необходимые для выполнения тех или иных операций, а скорость, определяемая косвенно по относительному числу операций, которые требуется провести для выполнения, например, деления или умножения в двоичной или прочих системах.
Если "p" - основание системы счисления, то максимальная цифра в одном разряде - (p-1).
Если N - максимальное число, то для его изображения требуется logpN разрядов.
Для того чтобы выполнить операцию умножения, например, потребуется (p-1)*logpN операций сложения. Если сравнить это число операций в системе с основанием "p" и отнести его к числу операций в системе с основанием "2", то может получиться следующая функция:
(p-1)*logpN p-1
___________ _____
f(p)= =
1*log2N log2p
| n
|
|
|
|
|
| ...
|
| | f(n)
| 1,000
| 1,262
| 1,500
| 1,725
| 1,913
| ...
| 2,709
| Это лишь основные соображения в пользу выбора в качестве основы двоичную систему счисления. Существуют и другие (контроль, диагностика неисправностей), но мы их из рассмотрения опустим.
| 
|
|



 x1x2x3
x1x2x3 


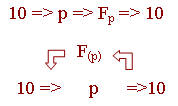 Т.е. нужно было бы из десятеричной системы перевести информацию в "p"-систему, произвести над ней необходимые операции в системе "p", затем снова сделать, но обратный перевод из "p"-системы в десятеричную, т.к. отказ от десятеричной системы потребовал бы и устранения первого этапа.
Если преобразование из десятеричной системы в "p"-систему требует не слишком много времени, в то же время, если выполнение функции F будет в системе "p" сделано много быстрее, то тогда эта цепочка действий будет оправданной.
Но для экономической информации характерно то, что очень несложные операции нужно производить всякий раз над большим объемом исходных данных. Так что в данном случае вряд ли целесообразно переходить к новой системе. Это и является объяснением того факта, что в настоящее время значительное число ЭВМ строится именно в десятеричной системе счисления.
Однако ЭВМ предназначены не только для выполнения экономических расчетов. В большинстве случаев неэкономических применений ЭВМ имеют дело с задачами, в которых общий объем исходных данных невелик, но общее число необходимых операций огромно. Именно для такого рода применений рассмотренная последовательность действий может оказаться выгодной.
Очевидно, что можно, не сужая области применения ЭВМ, задаться величиной некоторого самого большого числа. Пусть это будет число M. Воспользуемся позиционной системой счисления с основанием "p", и тогда потребуется "n" разрядов, чтобы представить все M чисел:
M = pn - 1 (от 0 до pn - 1)
M ≈ pn
logpM = n*logpp, где logpp = 1, тогда n = logpM.
Оборудование, которое нужно для хранения любого числа от 0 до M пропорционально произведению основания системы счисления на количество разрядов.
Таким образом, при заданном числе M количество цифроразрядов при основании "p":
p*n = p* logpM, (6.1)
где:
цифроразряд - эквивалент оборудования,
p*n - число устойчивых состояний элемента памяти,
n - число разрядов в числе.
Рассмотрим пример:
Пусть есть 24 цифроразряда.
Т.е. нужно было бы из десятеричной системы перевести информацию в "p"-систему, произвести над ней необходимые операции в системе "p", затем снова сделать, но обратный перевод из "p"-системы в десятеричную, т.к. отказ от десятеричной системы потребовал бы и устранения первого этапа.
Если преобразование из десятеричной системы в "p"-систему требует не слишком много времени, в то же время, если выполнение функции F будет в системе "p" сделано много быстрее, то тогда эта цепочка действий будет оправданной.
Но для экономической информации характерно то, что очень несложные операции нужно производить всякий раз над большим объемом исходных данных. Так что в данном случае вряд ли целесообразно переходить к новой системе. Это и является объяснением того факта, что в настоящее время значительное число ЭВМ строится именно в десятеричной системе счисления.
Однако ЭВМ предназначены не только для выполнения экономических расчетов. В большинстве случаев неэкономических применений ЭВМ имеют дело с задачами, в которых общий объем исходных данных невелик, но общее число необходимых операций огромно. Именно для такого рода применений рассмотренная последовательность действий может оказаться выгодной.
Очевидно, что можно, не сужая области применения ЭВМ, задаться величиной некоторого самого большого числа. Пусть это будет число M. Воспользуемся позиционной системой счисления с основанием "p", и тогда потребуется "n" разрядов, чтобы представить все M чисел:
M = pn - 1 (от 0 до pn - 1)
M ≈ pn
logpM = n*logpp, где logpp = 1, тогда n = logpM.
Оборудование, которое нужно для хранения любого числа от 0 до M пропорционально произведению основания системы счисления на количество разрядов.
Таким образом, при заданном числе M количество цифроразрядов при основании "p":
p*n = p* logpM, (6.1)
где:
цифроразряд - эквивалент оборудования,
p*n - число устойчивых состояний элемента памяти,
n - число разрядов в числе.
Рассмотрим пример:
Пусть есть 24 цифроразряда.



