
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия с комплексными числами в алгебраической форме
1) Сложение и вычитание:
2) Умножение: = 3) Деление: Пример. Даны два комплексных числа Произведем деление двух комплексных чисел:
Получаем значение заданного выражения: 16(- i)4 = 16 i 4 =16.
Геометрическая форма комплексного числа Понятие комплексного числа имеет геометрическое истолкование. Комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом ось ОХ будет являться действительной числовой осью, а ОУ - мнимой осью.
Практическое занятие №9 Наименование занятия: Действия над комплексными числами в тригонометрической и показательной формах. Цель занятия: Научиться выполнять действия над комплексными числами. Подготовка к занятию: Повторить теоретический материал по теме «Комплексные числа». Литература:
Задание на занятие:
1) Z = 5 i; 2) Z = -2 – 2 i; 3) Z = 4) Z = -6.
1) 2) 3) 4)
1) 2)
1) z 4 = i; 2) z4 + z 2 + 1 = 0. Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Тригонометрическая форма комплексного числа Показательная форма комплексного числа Величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа.
Действия с комплексными числами в тригонометрической и показательной формах Пусть комплексные числа В тригонометрической и показательной формах удобно производить следующие действия:
1. Умножение:
2. Деление: 3. Возведение в степень: 4. Извлечение корня из комплексного числа:
Корень n – ой степени из комплексного числа имеет n различных значений. Пример. Число
Число
При k = 0 получим При k = 1 получим При k = 2 получим При k = 3 получим
Практическое занятие №10 Наименование занятия: Вычисление пределов функций Цель занятия: Научиться вычислять пределы функций. Подготовка к занятию: Повторить теоретический материал по теме «Теория пределов. Непрерывность» Литература:
Задание на занятие: Вычислить пределы следующих функций: 1. 2. 3. 4. 5. 6. 7. 8.
9. 10. 11. 12. 13. 14. 15. 16. Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена). Число b называется пределом функции f(x) при х®а, если для любого e >0 существует такое число d(e) >0, что для всех х, удовлетворяющих неравенствам ï x - a ï < d и x ≠ a верно неравенство:ï f(x) - b ï< e.
Основные теоремы о пределах Теорема 1. Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а. Теорема 2. Теорема 3. Следствие. Теорема 4. Пример. Вычислить предел Сначала найдем предел знаменателя:
Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.31.209 (0.02 с.) |

 =
=
 . Для того, чтобы разделить одно комплексное число на другое, нужно числитель и знаменатель дроби домножить на число, сопряженное знаменателю:
. Для того, чтобы разделить одно комплексное число на другое, нужно числитель и знаменатель дроби домножить на число, сопряженное знаменателю:  =
= 
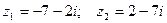 . Найти значение выражения
. Найти значение выражения  в алгебраической форме.
в алгебраической форме.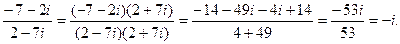

 и
и 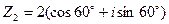 . Найти: Z 1· Z 2,
. Найти: Z 1· Z 2,  , (Z 2)4,
, (Z 2)4,  .
. ;
; ;
;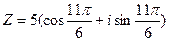 ;
;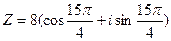 ;
;
 ;
; ;
;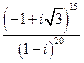


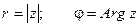 ;
; 
 ,
, 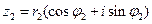 записаны в тригонометрической форме и
записаны в тригонометрической форме и  ,
,  - в показательной.
- в показательной. ;
; 
 ;
; 
 ;
; 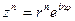 , где n – натуральное число.
, где n – натуральное число. ;
; 
 записать в тригонометрической форме, найти z20,
записать в тригонометрической форме, найти z20, 
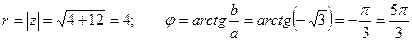 . Тогда
. Тогда  .
.





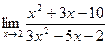 ;
;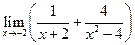 ;
;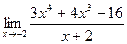 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;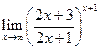
 ? Дать определение предела функции в точке.
? Дать определение предела функции в точке. ,
,  ?
?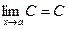 , где С = const.
, где С = const.
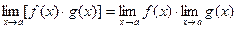

 при
при 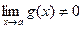
 .
. = 6∙12 = 6. Предел знаменателя отличен от нуля, следовательно, можно воспользоваться теоремами 4, 1:
= 6∙12 = 6. Предел знаменателя отличен от нуля, следовательно, можно воспользоваться теоремами 4, 1: =
=  =
=  =
=  =
= 
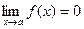 .
.


