
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация комплексного числа.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Как известно, действительные числа можно изображать точками числовой прямой. При этом каждому действительному числу соответствует единственная точка числовой прямой. Верно и обратное утверждение: каждой точке числовой прямой соответствует единственное действительное число. Значит, между точками числовой прямой и множеством всех действительных чисел установлено взаимно однозначное соответствие. Подобно тому, как действительные числа изображаются точками числовой прямой, комплексные числа можно изображать геометрически точками плоскости. Каждому комплексному числу а + вi поставили в соответствие точку плоскости с координатами А(а; в). Множество всех комплексных чисел находится во взаимно-однозначном соответствии с множеством всех точек плоскости. К любой точке плоскости можно провести радиус-вектор. Ось ОХ – действительная ось; ОУ – мнимая ось.
Операция комплексного сопряжения числа
Рис. 1. Комплексно сопряженные числа z и z * Операция комплексного сопряжения обладает следующими легко проверяемыми свойствами:
(Подразумевается, что если число находится в знаменателе дроби, то оно не равно нулю.) Из этих свойств вытекает важное следствие. Теорема. Пусть Доказательство. По условию теоремы справедливо тождество
Тогда выполняется и тождество
В виду вещественности коэффициентов ak,
что и завершает доказательство теоремы. Отметим, что вещественная x и мнимая y части комплексного числа
Прочитаем эту формулу справа налево:
Таким образом, квадрат суммы двух вещественных чисел можно разложить на линейные комплексные множители. -3- Показательная форма комплексного числа. Тогда от тригонометрической формы комплексного числа можно перейти к показательной форме: Тогда Примеры. Записать комплексное число в показательной форме. 1) 2) Возведение комплексного числа в целую степень
Пусть дано комплексное число. Для возведения комплексного числа в натуральную степень нужно возвести в эту степень его модуль, а аргумент умножить на показатель степени. Это правило известно в математике как формула Муавра:
Корни из комплексных чисел. Определение. Пусть Теорема. (Формула корней из комплексного числа.) Для любого ненулевого комплексного числа
где Доказательство. Обозначим
и докажем, что данное множество исчерпывает все множество корней n-йстепени из комплексного числа z. Доказательство проведем в 3 этапа. Сначала мы докажем, что всеэлементы множества (4) являются корнями n-й степени из комплексногочисла z. Затем мы покажем, что среди корней множества (4) нет равных. И, наконец, мы покажем, что любой корень n-й степени из комплексногочисла z является элементом множества (4). 1) По следствию 2 формулы Муавра
2) Допустим, что Но, аргумент числа 3) Пусть теперь комплексное число Далее, разделим целое число t на n с возможным остатком:
Теорема доказана. Пример. Вычислить Решение. Запишем число
Ответ:
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |


 заключается в изменении знака у мнимой части этого числа. Полученное число
заключается в изменении знака у мнимой части этого числа. Полученное число 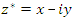 называется комплексно сопряженным числу
называется комплексно сопряженным числу 
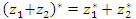


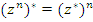
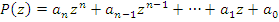 - многочлен целой степени n с вещественными коэффициентами ak, где k = 0, 1, 2,...
- многочлен целой степени n с вещественными коэффициентами ak, где k = 0, 1, 2,... 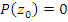 .
.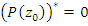 .
.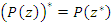 ,
,
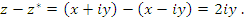
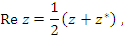
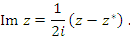
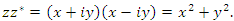

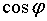 и
и 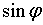 связаны формулой Эйлера:
связаны формулой Эйлера: 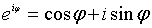 .
.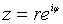 .
. Складывая и вычитая, легко получить
Складывая и вычитая, легко получить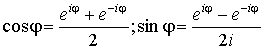 .
.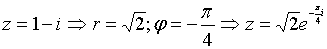

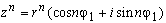
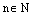 и
и  . Корнем n-й степени из комплексногочисла z называется комплексное число
. Корнем n-й степени из комплексногочисла z называется комплексное число 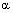 , такое, что
, такое, что 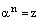 .
.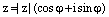 , где
, где  , существует ровно n корней n-й степенииз комплексного числа z и все они могут быть найдены по формуле
, существует ровно n корней n-й степенииз комплексного числа z и все они могут быть найдены по формуле , (3)
, (3)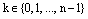 ,
, 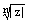 – арифметический корень n-й степени из положительного числа
– арифметический корень n-й степени из положительного числа 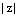 .
.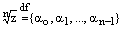 (4)
(4)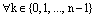
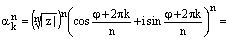
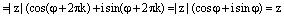 , ч.т.д.
, ч.т.д.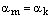 , где
, где 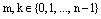 и
и 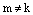 . Тогда по теореме о равенстве двух комплексных чисел в тригонометрической формезаписи следует, что равны их аргументы.
. Тогда по теореме о равенстве двух комплексных чисел в тригонометрической формезаписи следует, что равны их аргументы.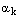 может отличаться от числа
может отличаться от числа  на числократное числу
на числократное числу 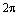 (т.е. на целое число оборотов) и аналогично для аргумента числа
(т.е. на целое число оборотов) и аналогично для аргумента числа 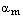 . Отсюда следует, что
. Отсюда следует, что  , где
, где 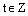 . Умножим это равенство на n:
. Умножим это равенство на n: 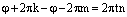 . Отсюда следует, что
. Отсюда следует, что 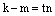 и т.к. по нашему предположению
и т.к. по нашему предположению 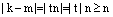 , чего не может быть, т.к.
, чего не может быть, т.к. 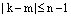 . Получили противоречие. Следовательно, среди корней вмножестве (10) нет равных, ч.т.д.
. Получили противоречие. Следовательно, среди корней вмножестве (10) нет равных, ч.т.д. является корнем n-й степени из комплексного числа z, т.е.
является корнем n-й степени из комплексного числа z, т.е. 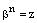 . Так как
. Так как  . Отсюда, из тех же соображений, что и во второй части доказательства, следуют равенства
. Отсюда, из тех же соображений, что и во второй части доказательства, следуют равенства  и
и  , где
, где 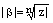 , а из второго следует
, а из второго следует 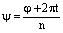 .
. , где
, где 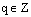 , а остаток r также является целым числом, но
, а остаток r также является целым числом, но 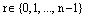 . Отсюда
. Отсюда и
и . Таким образом,корень
. Таким образом,корень  является корнем из множества корней (4), ч.т.д.
является корнем из множества корней (4), ч.т.д.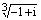 .
.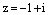 в тригонометрической форме записи:
в тригонометрической форме записи: 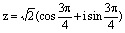 . Тогда
. Тогда , где
, где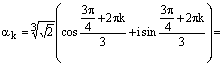
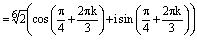 ,
, 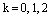 .
.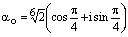 ,
, ,
,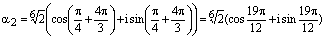 .
.


