
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вступ до теорії функції комплексного змінного.Содержание книги
Поиск на нашем сайте Вступ до теорії функції комплексного змінного. Тригонометрична і показникова Форми комплексних чисел.
Геометричним образом комплексного числа
Дійсна та уявна частини комплексного числа зв’язані з його модулем та аргументом співвідношеннями Як відомо, кожній точці координатної площини відповідає безліч значень полярного куту, які відрізняються одне від одного на Для однозначного визначення аргументу комплексного числа будемо обирати його з певного проміжку довжиною
З урахуванням наведених вище співвідношень комплексне число можна представити у вигляді
Така форма запису комплексного числа називається тригонометричною, а множення, ділення та піднесення до натурального степеня виконуються за формулами
З урахуванням формули Ейлера
Якщо комплексні числа записані у показниковій формі, то дії множення, ділення та піднесення до натурального степеня виконуються за правилами
Коренем
тобто корінь
Дії над комплексними числами Заданими в тригонометричній і показниковій формі Дійсна та уявна частини комплексного числа зв’язані з його модулем та аргументом співвідношеннями Як відомо, кожній точці координатної площини відповідає безліч значень полярного куту, які відрізняються одне від одного на Для однозначного визначення аргументу комплексного числа будемо обирати його з певного проміжку довжиною
З урахуванням наведених вище співвідношень комплексне число можна представити у вигляді
Така форма запису комплексного числа називається тригонометричною, а множення, ділення та піднесення до натурального степеня виконуються за формулами
З урахуванням формули Ейлера
Якщо комплексні числа записані у показниковій формі, то дії множення, ділення та піднесення до натурального степеня виконуються за правилами
Коренем
тобто корінь
Приклад. Записати комплексні числа у показниковій та тригонометричній формах. а) Розв’язок. Обчислимо модуль та головне значення аргумента комплексного числа.
Тоді та
б) Розв’язок.
Тоді та Елементи лінійної алгебри.
Визначники вищих порядків. Теорема 1.1 (Лапласа). Визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на їх алгебраїчні доповнення. Наприклад, для визначника третього порядку виконуються такі рівності: Теорема 1.2. Сума добутків елементів довільного рядка (стовпця) на алгебраїчні доповнення іншого рядка (стовпця) дорівнює нулю. Наприклад, для визначника третього порядку виконуються такі рівності:
N.B. Теореми 1.1 і 1.2 мають місце для визначників будь-якого порядку. Розглянемо визначник n-го порядку
За теоремою 1.1 цей визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на їх алгебраїчні доповнення. Наприклад, розклад визначника за елементами першого рядка такий:
Def. Визначником n-го порядку
називають алгебраїчну суму всіх можливих добутків, які містять по одному елементу з кожного рядка і кожного стовпця. Знак кожного доданка дорівнює Усього таких доданків n! Половину з них беруть зі знаком плюс, а іншу половину – зі знаком мінус. N.B. Визначник n-го порядку, у якого під головною діагоналлю всі елементи нульові, дорівнює добутку елементів головної діагоналі, тобто
Ранг матриці. Нехай задано матрицю Ат х п = А. Виділимо в матриці А будь-які k рядків і стільки ж стовпців, де k — число, не більше чисел т і п, тобто k Визначник порядку k, складений з елементів, що стоять на перетині виділених рядків і стовпців, називається мінором k -гo порядку матриці А. Рангом r (А) матриці А називається найбільший з порядків її мінорів, відмінних від нуля. Безпосередньо з означення випливає, що: 1) Ранг існує для будь-якої матриці Ат х п , причому
2) r (A) = 0 тоді і тільки тоді, коли А = 0; 3) для квадратної матриці п -го порядку ранг дорівнює п тоді і тільки тоді, коли матриця невироджена. Ранг матриці можна знайти так. Якщо всі мінори першого порядку (елементи матриці) дорівнюють нулю, то r = 0. Якщо хоч один з мінорів першого порядку відмінний від нуля, а всі мінори другого порядку дорівнюють нулю, то r = 1. У випадку, коли є мінор другого порядку, відмінний від нуля, досліджуємо мінори третього порядку. Так продовжуємо доти, поки не станеться одне з двох: або всі мінори порядку k дорівнюють нулю, або мінорів порядку k не існує, тоді r = k- l. Приклад Знайти ранг матриці
О Серед мінорів першого порядку (тобто елементів матриці) є відмінні від нуля) тому r (А) Оскільки один з мінорів другого порядку
а всі мінори третього порядку дорівнюють нулю, то r (А) = 2. • Вказаний метод знаходження рангу матриці не завжди зручний, тому що пов'язаний з обчисленням значного числа визначників. Простіший метод ґрунтується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме [1]: а) переставити місцями два рядки (стовпці); б) помножити кожен елемент рядка (стовпця) на один і той самий відмінний від нуля множник; в) додати до елементів рядка (стовпця) відповідні елементи другого рядка (стовпця), помножені на одне і те саме число. Розглянемо довільну (не обов’язково квадратну) матрицю A. Рангом r (A) цієї матриці називається найвищий порядок її мінора, що не дорівнює нулю. Приклад. Матриця
Обернена матриця. Матриця А -1 називається оберненою до квадратної матриці А, якщо добуток цих матриць дорівнює одиничній матриці, тобто АА-1=А-1А=Е.
Обернена матриця існує для всякої квадратної матриці А, яка є невиродженою, тобто коли визначник матриці detA ≠ 0.
Алгоритм знаходження оберненої матриці:
1. Обчислити визначник матриці А. Якщо detA ≠ 0, то матриця А має обернену, в іншому випадку оберненої матриці не існує. 2. знайти транспоновану матрицю АТ 3. Обчислити алгебричні доповнення Аij елементів матриці АТ. 4. Визначити обернену матрицю за формулою:
1. Знайти матрицю, обернену до матриці Розв’язання: Знайдемо визначник матриці:
Перевіримо, чи виконуються рівності
Отже
Теорема Кронекера-Капеллі. Основні визначення Системою m лінійних рівнянь з n змінними x1, x2, …, xn називається система, яка має наступний вигляд: де аij – коефіцієнти при змінних; bi -вільні члени, Упорядкована сукупність чисел Система, що має розв’язок, називається сумісною. Система, яка не має жодного розв’язку, називається несумісною. Система з єдиним розв’язком називається визначеною, а з більшим числом розв’язків – невизначаною. Система двох лінійних рівнянь з двома змінними має вигляд:
а систему трьох лінійних рівнянь з трьома змінними записують у вигляді: Система рівнянь називається однорідною, якщо всі вільні члени дорівнюють нулю, і неоднорідною, якщо хоч один з них відмінний від нуля. Множина чисел аіа2,...,а п називається впорядкованою, якщо вказані порядок слідування цих чисел, яке з них є першим, яке другим, яке третім... Упорядкований набір п чисел називається розв'язком системи, якщо при підстановці цих чисел замість невідомих х1 х2, х п рівняння системи перетворюються у тотожні. Таку систему чисел називають також n-вимірним вектором, або точкою n-вимірного простору. Система рівнянь називається сумісною, якщо вона має хоч один розвязок, і несумісною, якщо вона не має жодного розв'язку. Сумісна система називається визначеною, якщо вона має один розв'язок. Сумісна система називається невизначеною, якщо вона має більше ніж один розв”язок. Дві системи лінійних рівнянь називаються еквівалентними, якщо вони мають одну множину розв'язків. Еквівалентні системи дістають внаслідок елементарних перетворень даної системи. Елементарні перетворення системи лінійних рівнянь відповідають елементарним перетворенням матриці, за умови, якщо вони виконуються над рядкам матриці.
Формули Крамера. Це правило можна застосувати, якщо кількість рівнянь і кількість невідомих співпадають. Для простоти викладу розглянемо систему трьох лінійних рівнянь з трьома невідомими (
Позначимо визначники:
Визначник Якщо
і такий спосіб визначення невідомих називають правилом Крамера. Якщо Якщо
Приклад. Розв’язати систему лінійних рівнянь методом Крамера:
Розв’язання. Складемо і обчислимо визначники:
Підставимо одержані результати у формули (6). Маємо
Відповідь:
Метод Гауса. Для розв’язування систем лінійних рівнянь застосовують метод, який називають методом Гаусса або методом виключення змінних. Суть методу Гаусса розв’язування систем лінійних рівнянь розглянемо за допомогою матриць. Його ідея полягає у зведенні розширеної матриці системи за допомогою елементарних перетворень матриці до трикутної матриці.
Трикутною називають матрицю, у якої під головною діагоналлю всі елементи рівні нулю.
Елементарними перетвореннями матриці є такі перетворення: 1) перестановка двох рядків матриці; 2) множення всіх елементів рядка на одне і те ж число, відмінне від нуля; 3) додавання елементів якого-небудь рядка матриці, помножених на одне і те ж число, до відповідних елементів іншого рядка; 4) відкидання рядків матриці, елементами яких є нулі.
Проводячи елементарні перетворення над матрицею системи, отримують нову систему рівнянь, яка еквівалентна заданій, але з новими коефіцієнтами та вільними членами. Одержують трикутну систему рівнянь, із якої визначають невідомі.
Приклад. Методом Гаусса розв’язати систему лінійних рівнянь
Розв’язання. Складемо розширену матрицю системи і будемо робити над нею необхідні елементарні перетворення, щоб одержати трикутну матрицю. На початку переставимо перше і третє рівняння місцями, а потім помножимо елементи першого рядка відповідно на мінус три, мінус два та мінус два і одержані результати додамо відповідно до елементів другого, третього та четвертого рядків. Аналогічно вчинимо з елементами другого, а потім третього рядків. Одержимо матрицю
~ Система лінійних рівнянь матиме вигляд
З третього рівняння Відповідь:
І її розв’язування. Матричний спосіб можна застосувати, якщо кількість рівнянь і кількість невідомих співпадають, а крім того, матриця системи має обернену.
Запишемо систему (5) у матричному вигляді. Для цього введемо матриці виду:
Користуючись правилом множення матриць, систему (5) запишемо у матричному вигляді
Розв’язок цього рівняння має вигляд
де
Приклад. Розв’язати систему лінійних рівнянь матричним способом.
Розв’язання. Перепишемо задану систему у вигляді (7). Для цього складемо матриці виду
Розв’язок системи будемо шукати у вигляді (8). Необхідно знайти обернену матрицю
Складемо обернену матрицю згідно формули (3). Одержимо
Помножимо обернену матрицю на матрицю
Відповідь:
Аналітична геометрія.
Додавання векторів.
Щоб побудувати суму даних векторів  і і  , треба відкласти ці вектори від довільної точки та побудувати на них паралелограм. Сумою векторів буде діагональ, що виходить з початку векторів , треба відкласти ці вектори від довільної точки та побудувати на них паралелограм. Сумою векторів буде діагональ, що виходить з початку векторів  і і  (рис. 3.1). (рис. 3.1).
Цей спосіб побудови називається правилом паралелограма. Суму двох векторів можно побудувати ще й за правилом трикутника.
Відкласти вектор  від кінця вектора від кінця вектора  . Сумою векторів . Сумою векторів  і і  буде вектор, що з’єднує початок буде вектор, що з’єднує початок  з кінцем з кінцем  (рис. 3.2). (рис. 3.2).
Щоб побудувати суму n даних векторів  , треба від довільної точки відкласти , треба від довільної точки відкласти  , потім від його кінця відкласти , потім від його кінця відкласти 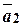 і т.д., нарешті від кінця і т.д., нарешті від кінця  відкласти відкласти  . Сумою векторів буде вектор, напрямлений від початку . Сумою векторів буде вектор, напрямлений від початку  до кінця до кінця  (рис. 3.3). (рис. 3.3).
Віднімання векторів.
Щоб побудувати різницю векторів  , треба відкласти ці вектори від довільної точки, з’єднати їх кінці та вибрати на цьому відрізку напрямок від кінця , треба відкласти ці вектори від довільної точки, з’єднати їх кінці та вибрати на цьому відрізку напрямок від кінця  до кінця до кінця  (рис. 3.4). (рис. 3.4).
Множення вектора на число. Добутком ненульового вектора Ці три операції називаються лінійними операціями з векторами. Проекція вектора на вісь.
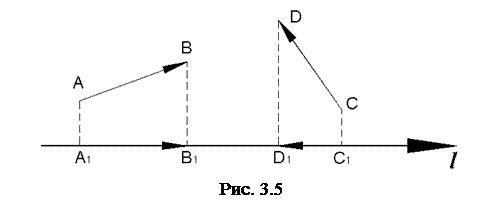
Проекцією вектора на вісь називається довжина направленого відрізка, початок якого є проекція початку вектора і кінець – проекція його кінця, яка береться із знаком плюс, якщо напрями відрізка і осі збігаються, і зі знаком мінус, якщо їх напрями протилежні (рис.3.5).
Властивості проекції. a) б) в) В просторі
Диференціальне числення. Числова послідовність. Основні теореми про границі 1) Якщо функції
В останньому випадку припускається, що функція
2) Якщо при 3) Якщо при
Визначні границі. В теорії границь важливе місце займають перераховані нижче границі 1)-4) за допомогою яких обчислюється багато границь від елементарних функцій: · 1) · 2) · 3) · 4)
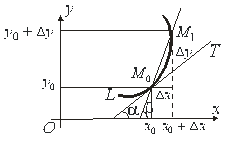
Вступні відомості Нехай матеріальна точка рухається прямолінійно, а закон руху її задається деякою функцією 1. Поставимо задачу: знайти швидкість точки в момент часу Нехай в деякий момент часу Відношення називається середньою швидкістю руху точки. Означення. Швидкістю Зазначимо, що формула дає змогу знайти швидкість у момент часу
Рис.6.1 2. Задача про дотичну до кривої. З поняттям дотичної до кривої в даній точці ми зустрічалися при вивченні кола за шкільною програмою, за якою давалося означення дотичної до кола як прямої лінії, що має з колом одну спільну точку. Проте це означення є окремим випадком. Його не можна поширити, наприклад, на незамкнуті криві. Тому треба дати загальне означення дотичної, яке б підходило як до замкнутих, так і до незамкнутих кривих. Нехай маємо деяку довільну криву
Рис.6.2 Рис.6.3 Означення. Дотичною до кривої
Рис.6.4
Означення похідної Нехай функція
Якщо границя (4.1) існує і скінченна, вона називається похідною функції
Означення. Похідною функції Операція знаходження похідної називається диференціюванням цієї функції. Користуючись означенням похідної, знайти похідні функцій. Приклад. Функція у = х 2. Знайти похідну в точках х = 3 і х = – 4. l Надамо аргументу х приросту Складемо відношення приросту функції до приросту аргументу | |||||||||||||||
|
| Поделиться: |

 є точка на координатній площині з відповідними декартовими координатами. Полярні координати цієї точки також є важливими характеристиками комплексного числа. Відповідний полярний радіус називається модулем комплексного числа, а полярний кут – його аргументом:
є точка на координатній площині з відповідними декартовими координатами. Полярні координати цієї точки також є важливими характеристиками комплексного числа. Відповідний полярний радіус називається модулем комплексного числа, а полярний кут – його аргументом: ,
, 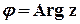 .
.

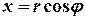 ,
,  .
.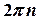 , де
, де  – ціле число.
– ціле число. . Таке значення аргументу називається його головним значенням та позначається
. Таке значення аргументу називається його головним значенням та позначається  . Будемо вважати, що
. Будемо вважати, що 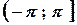 (досить часто також використовують проміжок
(досить часто також використовують проміжок  ).Тоді модуль та головне значення аргументу комплексного числа доцільно обчислювати за формулами
).Тоді модуль та головне значення аргументу комплексного числа доцільно обчислювати за формулами ;
;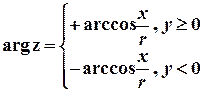 або
або  .
. .
. ;
; ;
; .
. комплексне число може бути записано у показниковій формі
комплексне число може бути записано у показниковій формі .
. ;
; ;
; .
. називається таке число,
називається таке число,  ,
,  ,
, .
. ,
,  .
.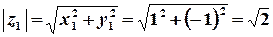 ;
; , або
, або .
. – тригонометрична форма,
– тригонометрична форма, – показникова форма.
– показникова форма.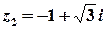 .
. ,
, 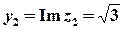 ;
; ;
; , або
, або .
. – тригонометрична форма,
– тригонометрична форма, – показникова форма.
– показникова форма. (розклад за елементами першого рядка);
(розклад за елементами першого рядка); (розклад за елементами другого стовпця).
(розклад за елементами другого стовпця). ,
,  .
. .
.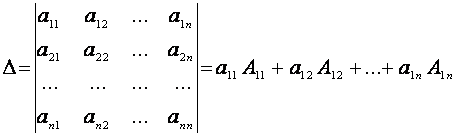 .
. , де
, де  – число інверсій у других індексах за умови, що елементи (множники
– число інверсій у других індексах за умови, що елементи (множники  ) доданка розміщені в порядку зростання перших індексів. Отже,
) доданка розміщені в порядку зростання перших індексів. Отже, .
.
 min (т, п).
min (т, п).

 1.
1.
 має три мінори третього поряду (всі з яких дорівнюють нулю), дев’ять мінорів другого порядку (з яких деякі дорівнюють нулю, а деякі – ні) та 12 мінорів першого порядку. Отже, для цієї матриці ранг r (A)=2.
має три мінори третього поряду (всі з яких дорівнюють нулю), дев’ять мінорів другого порядку (з яких деякі дорівнюють нулю, а деякі – ні) та 12 мінорів першого порядку. Отже, для цієї матриці ранг r (A)=2. .
. і перевірити, чи справджуються рівності
і перевірити, чи справджуються рівності  .
. .Оскільки
.Оскільки  , обернена матриця
, обернена матриця  існує. Знаходимо алгебричні доповнення: А11= 3, А12= -1, А21 = -2, А22 = 1. Тоді обернена матриця буде мати вигляд:
існує. Знаходимо алгебричні доповнення: А11= 3, А12= -1, А21 = -2, А22 = 1. Тоді обернена матриця буде мати вигляд: 
 .
. ;
; .
.

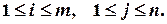
 , називається розв’язком системи, якщо при заміні х1 на а1, х2 на а2, …, хn на аn у кожному рівнянні системи дістанемо n правильних числових рівностей.
, називається розв’язком системи, якщо при заміні х1 на а1, х2 на а2, …, хn на аn у кожному рівнянні системи дістанемо n правильних числових рівностей. (2.1)
(2.1)
 ):
):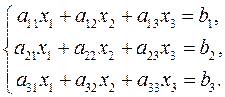 (5)
(5)

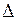 називають визначником системи і його складають з коефіцієнтів при невідомих, а у визначниках
називають визначником системи і його складають з коефіцієнтів при невідомих, а у визначниках 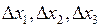 коефіцієнти при відповідних невідомих замінені вільними членами.
коефіцієнти при відповідних невідомих замінені вільними членами. , то система (5) має єдиний розв’язок. Невідомі визначають за формулами
, то система (5) має єдиний розв’язок. Невідомі визначають за формулами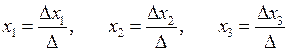 (6)
(6)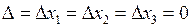 , то система (5) має безліч розв’язків, а правило Крамера застосувати не можна.
, то система (5) має безліч розв’язків, а правило Крамера застосувати не можна. , а хоча б один із визначників
, а хоча б один із визначників 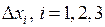 , відмінний від нуля, то система (5) несумісна.
, відмінний від нуля, то система (5) несумісна.




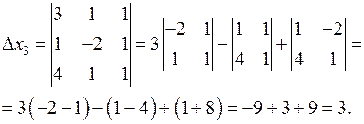

 .
.
 ~
~ 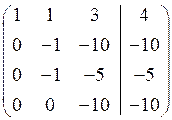 ~
~ 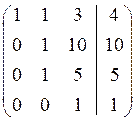 ~
~ ~
~  ~
~  ~
~  .
.
 . З другого рівняння одержали
. З другого рівняння одержали  , а з першого одержуємо
, а з першого одержуємо 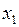 .
. .
. .
.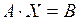 . (7)
. (7) , (8)
, (8) є оберненою матрицею до матриці
є оберненою матрицею до матриці  .
.
 (див. приклад 2). Знайдемо алгебраїчні доповнення для кожного елемента матриці
(див. приклад 2). Знайдемо алгебраїчні доповнення для кожного елемента матриці 
 .
. і одержимо шукану матрицю
і одержимо шукану матрицю  . Маємо
. Маємо .
.



 , і протинапрям, якщо
, і протинапрям, якщо  (при
(при  ,
,  ).
).
 ,
,  .
. ;
;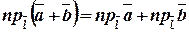 ;
; .
.


 і
і  мають границі при
мають границі при  , який прямує до
, який прямує до  , то функції
, то функції  ,
,  ,
,  також мають границі при
також мають границі при  ,
, ,
, .
. .
.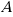 , і ця границя більше числа
, і ця границя більше числа  , то для достятньо близьких до
, то для достятньо близьких до  .
. функція
функція  має границю A, то ця границя єдина.
має границю A, то ця границя єдина. .
.
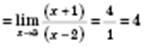 .
. можна, тому що в означенні границі
можна, тому що в означенні границі  .
. — перша визначна границя.
— перша визначна границя.
 .
.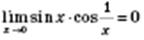 .
. , а функція
, а функція 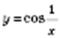 є обмеженою.
є обмеженою.  ,
, ,
, ,
, 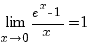 ,
, ,
, 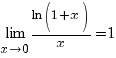 .
.
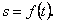 (6.1)
(6.1) .
. (рис.6.1).Через проміжок часу
(рис.6.1).Через проміжок часу  точка займе положення
точка займе положення  і пройде шлях
і пройде шлях  .
. (6.2)
(6.2) точки в момент часу
точки в момент часу  на проміжку часу
на проміжку часу  (6.3)
(6.3)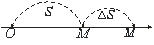
 (рис.6.2, 6.3). Візьмемо на цій кривій точки
(рис.6.2, 6.3). Візьмемо на цій кривій точки  та
та  і через них проведемо пряму
і через них проведемо пряму  , яку називатимемо січною. Якщо точка
, яку називатимемо січною. Якщо точка  , рухаючись вздовж кривої, наближається до точки
, рухаючись вздовж кривої, наближається до точки  прямує до нуля. Якщо при цьому й значення кута
прямує до нуля. Якщо при цьому й значення кута  прямує до нуля, то пряма
прямує до нуля, то пряма  називається граничним положенням січної
називається граничним положенням січної 
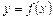 визначена на деякому проміжку (а; b). Візьмемо значення
визначена на деякому проміжку (а; b). Візьмемо значення  і надамо аргументу приросту
і надамо аргументу приросту  . Тоді функція набуде приросту
. Тоді функція набуде приросту  . Розглянемо відношення приросту функції
. Розглянемо відношення приросту функції 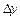 до приросту аргументу
до приросту аргументу  :
: . (4.1)
. (4.1)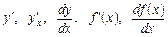 .
. за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.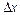 , тоді функція набуде приросту
, тоді функція набуде приросту 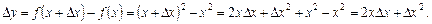
 , відшукаємо границю
, відшукаємо границю 


