
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про лінію та її рівняння.Содержание книги
Поиск на нашем сайте
Лінія на площині розглядається (задається) як множинаточок,що має певні і притаманні тільки їм геометричні властивості. Наприклад, коло радіусом R це безліч всіх точок площини, віддалених на відстань R від деякої фіксованої точки О (центра кола). Введення на площині системи координат дозволяє визначати положення точки площини завданням двох чисел — її координат, а положення лінії на площині визначається за допомогою рівняння (тобто рівність, що зв'язує координати точок лінії). Рівняння лінії (або кривої) на площині Оху називається таке рівняння F(х;у)=0 з двома змінними, якому задовольняють координати х і у кожної точці лінії і не задовольняють координати будь-якої точки, які не лежать на цій лінії. Змінні x і у в рівнянні лінії називаються поточними координатами точок лінії. Рівняння лінії дозволяє вивчення геометричних властивостей лінії замінити дослідженням його рівняння. Так, для того, щоб встановити чи лежить точка A(x0; y0) на даній лінії, досить перевірити (не вдаючись до геометричних побудов), чи задовольняють координати точки А рівнянню цієї лінії у вибраній системі координат. Приклад: Чи лежать точки К(—2; 1) і L(1; 1) на лінії ○ Підставивши в рівняння замість x і у координати точки К, отримаємо Завдання про знаходження точок перетину двох ліній, заданих рівняннями F1(х; у)=0 і F2(х; у)=0, зводиться до відшукування точок, координати яких задовольняють рівняння обох ліній, тобто зводиться до розв’язку системи двох рівнянь з двома невідомими: Якщо ця система не має дійсних розв’язок, то лінії не перетинаються. Аналогічним чином вводиться поняття рівняння лінії в полярній системі координат. Рівняння F(
де х і у — координати довільної точки М(х; у), які лежать на даній лінії, а t — змінна, називається параметром; параметр t визначає положення точки (х; у) на площині. Наприклад, якщо Якщо параметр t змінюється, то точка на площині переміщається, описуючи дану лінію. Такий спосіб завдання прямої називається параметричним, а рівняння (2.1) — параметричними рівняннями лінії. Щоб перейти від параметричних рівнянь лінії до рівняння виду F(х;у)=0, треба яким-небудь чином з двох рівнянь виключити параметр t. Наприклад, від параметричних рівнянь
рис. 9. Лінію на площині можна задати векторним рівнянням, де t — скалярний змінний параметр. Кожному значенню t0 відповідає певний вектор Векторному рівнянню лінії Векторне рівняння і параметричне рівняння лінії мають механічний сенс. Якщо точка переміщається на площині, то вказані рівняння називаються рівняннями руху, а пряма — траєкторією точки, параметр t при цьому є час. Отже, всякій лінії на площині відповідає деяке рівняння виду F(х; у)= 0. Всякому рівнянню виду F(х; у)= 0 відповідає, взагалі кажучи, деяка лінія, властивості якої визначаються даним рівнянням (вираз «взагалі кажучи» означає, що сказане допускає виключення. Так, рівнянню (х-2)2+(у-3)2=0 відповідає не лінія, а точка (2;3); рівнянню У аналітичній геометрії на площині виникають два основні завдання. Перше: знаючи геометричні властивості кривої, знайти її рівняння; друге: знаючи рівняння кривої, вивчити її форму і властивості. На малюнках 10-18 приведені приклади деяких кривих і вказані їх рівняння.
рис. 10. Коло радіусом R
рис. 11. Лемніската Бернуллі рис. 12. Трьохпелюсткова роза у полярних координатах:
рис. 13. Равлик Паскаля Рівняння в полярних координатах має вигляд
рис. 14. Напівкубічна парабола рис. 15. Астроїда Рівняння кривої у2 = х3 або Рівняння в прямокутних координатах:
рис. 16. Кардіоїда рис. 17. Спіраль Архімеда Рівняння в полярних координатах рівняння кривої в полярних має вигляд де равлика Паскаля (
рис. 18. Циклоїда Параметричні рівняння циклоїди мають вигляд Циклоїда — це крива, яку описує фіксована точка кола, що котиться без ковзання по нерухомій прямій.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 996; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.72.220 (0.006 с.) |

 ?
? . Отже, точки К лежить на даній лінії. Точка L не лежить на даній лінії, оскільки
. Отже, точки К лежить на даній лінії. Точка L не лежить на даній лінії, оскільки  .●
.● ;
;  )=0 називається рівнянням даної лінії в полярній системі координат, якщо координати будь-якої точки, лежать на цій лінії, і лише вони, задовольняють це рівняння. Пряму на площині можна задати за допомогою двох рівнянь:
)=0 називається рівнянням даної лінії в полярній системі координат, якщо координати будь-якої точки, лежать на цій лінії, і лише вони, задовольняють це рівняння. Пряму на площині можна задати за допомогою двох рівнянь: (2.1)
(2.1) ,
,  у, то значенню параметра
у, то значенню параметра  відповідає на площині точка з координатами (3; 4), оскільки
відповідає на площині точка з координатами (3; 4), оскільки  ,
,  .
. шляхом підстановки
шляхом підстановки  в друге рівняння, легко отримати рівняння
в друге рівняння, легко отримати рівняння  або
або  , тобто виду F(х; у)= 0. Проте, відмітимо, такий перехід не завжди доцільний і не завжди можливий.
, тобто виду F(х; у)= 0. Проте, відмітимо, такий перехід не завжди доцільний і не завжди можливий.

 опише деяку лінію (див. рис. 9).
опише деяку лінію (див. рис. 9). на площині не відповідає ніякий геометричний образ).
на площині не відповідає ніякий геометричний образ).




 або
або 
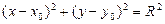


 2(х2–у2)=0,
2(х2–у2)=0,  > 0; має вигляд,
> 0; має вигляд,  де >0.
де >0.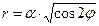 .
.
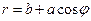 .
.

 ; параметричні рівняння:
; параметричні рівняння:



 , координатах,
, координатах, 
 . Кардіоїда — окремий випадок де
. Кардіоїда — окремий випадок де  ).
).
 де а > 0.
де а > 0.


