
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення визначників вищих порядків.Содержание книги
Поиск на нашем сайте
Визначник п порядку дорівнює сумі добутків усіх елементів будь-якого стовпця (або рядка) на відповідні їм алгебраїчні доповнення. У випадку використання і -го рядка це правило математично виглядає так
Цю рівність називають розкладом визначника за елементами і-го рядка. Обчислення визначника п порядку зводиться до обчислення п визначників (п-1) порядку. Для скорочення обчислень визначник доцільно розкладати за елементами рядка або стовпця, який містить найбільшу кількість нулів. До нулів не треба знаходити алгебраїчних доповнень тому, що добуток 0 на його алгебраїчне доповнення дорівнює нулю. Властивості визначника дозволяють робити еквівалентні перетворення визначника і одержувати якомога більше нулів в деякому рядку або стовпці. 1. Обчисліть визначник
Розклавши цей визначник по елементах 1-го стовпця, маємо
Додамо до елементів 1-го рядка елементи 3-го рядка і віднімемо від елементів 2-го рядка елементи 3-го рядка, одержимо
Розкладемо визначник по елементах 1-го стовпця.
2. Обчисліть визначник п’ятого порядку
Одержимо:
Розкладемо визначник по елементах другого стовпця.
В одержаному визначнику вже 4-го порядку з найменших елементів складається 4-ий рядок. Перетворимо в нулі всі його елементи, крім а42=-1. Для цього виконаємо (Іст+(-3)ІІст, ІІІст+2 ІІст, ІVст+3 ІІст). В результаті одержимо:
Розкладемо визначник по елементах четвертого рядка
(Ми винесли за знак визначника спільний множник з елементів другого рядка і спільний множник з елементів третього рядка). Для зменшення елементів цього визначника додамо перший стовпець до другого та третього:
3. Обчислити визначник n-го порядку, звівши його до трикутного вигляду:
Δ Віднімемо І рядок від усіх інших.
Ранг матриці. Нехай задано матрицю Ат х п = А. Виділимо в матриці А будь-які k рядків і стільки ж стовпців, де k — число, не більше чисел т і п, тобто k Визначник порядку k, складений з елементів, що стоять на перетині виділених рядків і стовпців, називається мінором k -гo порядку матриці А. Рангом r (А) матриці А називається найбільший з порядків її мінорів, відмінних від нуля. Безпосередньо з означення випливає, що: 1) Ранг існує для будь-якої матриці Ат х п , причому
2) r (A) = 0 тоді і тільки тоді, коли А = 0; 3) для квадратної матриці п -го порядку ранг дорівнює п тоді і тільки тоді, коли матриця невироджена. Ранг матриці можна знайти так. Якщо всі мінори першого порядку (елементи матриці) дорівнюють нулю, то r = 0. Якщо хоч один з мінорів першого порядку відмінний від нуля, а всі мінори другого порядку дорівнюють нулю, то r = 1. У випадку, коли є мінор другого порядку, відмінний від нуля, досліджуємо мінори третього порядку. Так продовжуємо доти, поки не станеться одне з двох: або всі мінори порядку k дорівнюють нулю, або мінорів порядку k не існує, тоді r = k- l. Приклад Знайти ранг матриці
О Серед мінорів першого порядку (тобто елементів матриці) є відмінні від нуля) тому r (А) Оскільки один з мінорів другого порядку
а всі мінори третього порядку дорівнюють нулю, то r (А) = 2. • Вказаний метод знаходження рангу матриці не завжди зручний, тому що пов'язаний з обчисленням значного числа визначників. Простіший метод ґрунтується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме [1]: а) переставити місцями два рядки (стовпці); б) помножити кожен елемент рядка (стовпця) на один і той самий відмінний від нуля множник; в) додати до елементів рядка (стовпця) відповідні елементи другого рядка (стовпця), помножені на одне і те саме число. Розглянемо довільну (не обов’язково квадратну) матрицю A. Рангом r (A) цієї матриці називається найвищий порядок її мінора, що не дорівнює нулю. Приклад. Матриця
Обернена матриця. Матриця А -1 називається оберненою до квадратної матриці А, якщо добуток цих матриць дорівнює одиничній матриці, тобто АА-1=А-1А=Е.
Обернена матриця існує для всякої квадратної матриці А, яка є невиродженою, тобто коли визначник матриці detA ≠ 0.
Алгоритм знаходження оберненої матриці:
1. Обчислити визначник матриці А. Якщо detA ≠ 0, то матриця А має обернену, в іншому випадку оберненої матриці не існує. 2. знайти транспоновану матрицю АТ 3. Обчислити алгебричні доповнення Аij елементів матриці АТ. 4. Визначити обернену матрицю за формулою:
1. Знайти матрицю, обернену до матриці Розв’язання: Знайдемо визначник матриці:
Перевіримо, чи виконуються рівності
Отже
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.232 (0.009 с.) |



 Виконаємо такі дії: 1) до елементів 1-го рядка додамо помножені на -3 відповідні елементи 2-го рядка; 2) до елементів 3-го рядка додамо подвоєні елементи 2-го рядка; 3) до елементів 4-го рядка додамо відповідні елементи 2-го рядка, помножені на -1. Тоді вихідний визначник перетвориться до вигляду.
Виконаємо такі дії: 1) до елементів 1-го рядка додамо помножені на -3 відповідні елементи 2-го рядка; 2) до елементів 3-го рядка додамо подвоєні елементи 2-го рядка; 3) до елементів 4-го рядка додамо відповідні елементи 2-го рядка, помножені на -1. Тоді вихідний визначник перетвориться до вигляду.





 Для перетворення в нуль всіх елементів (крім одного) будь-якого рядка чи стовпця, вибираємо той рядок або стовпчик, який складається з найменших чисел. У визначнику таким буде другий стовпчик. Залишимо в ньому без змін елемент а22=-1, а всі інші перетворимо в нулі. Для цього виконаємо:
Для перетворення в нуль всіх елементів (крім одного) будь-якого рядка чи стовпця, вибираємо той рядок або стовпчик, який складається з найменших чисел. У визначнику таким буде другий стовпчик. Залишимо в ньому без змін елемент а22=-1, а всі інші перетворимо в нулі. Для цього виконаємо: 




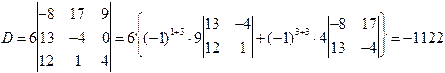
 Останній визначник розклали по елементах третього стовпця.
Останній визначник розклали по елементах третього стовпця. .
. До І стовпця додамо суму всіх інших.
До І стовпця додамо суму всіх інших.

 min (т, п).
min (т, п).

 1.
1.
 має три мінори третього поряду (всі з яких дорівнюють нулю), дев’ять мінорів другого порядку (з яких деякі дорівнюють нулю, а деякі – ні) та 12 мінорів першого порядку. Отже, для цієї матриці ранг r (A)=2.
має три мінори третього поряду (всі з яких дорівнюють нулю), дев’ять мінорів другого порядку (з яких деякі дорівнюють нулю, а деякі – ні) та 12 мінорів першого порядку. Отже, для цієї матриці ранг r (A)=2. .
. і перевірити, чи справджуються рівності
і перевірити, чи справджуються рівності  .
. .Оскільки
.Оскільки  , обернена матриця
, обернена матриця  існує. Знаходимо алгебричні доповнення: А11= 3, А12= -1, А21 = -2, А22 = 1. Тоді обернена матриця буде мати вигляд:
існує. Знаходимо алгебричні доповнення: А11= 3, А12= -1, А21 = -2, А22 = 1. Тоді обернена матриця буде мати вигляд: 
 .
. ;
; .
.


