
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деякі інтеграли, що не виражаються через елементарні функціїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Як вже наголошувалося вище, операція інтегрування функцій значно складніша за операцію диференціювання функцій. Не завжди вибраний шлях інтегрування є найкращим, більш коротким, простим. Інтегрування часто може бути виконане не єдиним способом. Багато що залежить від рекомендованого знання багатьох штучних прийомів інтегрування, від кмітливості, від натренованості. Наприклад,
Навряд чи варто обчислювати інтеграл
Помітивши, що чисельник
На практиці при обчисленні невизначених інтегралів використовують різні довідники, що містять таблиці інтегралів, які часто зустрічаються. Зокрема, «Таблиці невизначених інтегралів» М.Л.Смолянського. Вивчені методи інтегрування дозволяють у багатьох випадках обчислити невизначений інтеграл, тобто знайти первісну функцію для підінтегральної функції. Як відомо, всяка неперервна функція має первісну. У тому випадку, коли первісна деякої елементарної функції Так, наприклад, не можна узяти інтеграл
Первісні від функції
Інтеграли Ейлера. При
При
Інтеграл Фур’є. Якщо 1) функція (4) де Якщо визначити амплітуду
Для комплекснозначних функцій розклад (4) має вигляд:
Завдання Користуючись класичними невласними інтегралами (Пуассона, Діріхле, Фруллані, Френеля) та властивостями невласних інтегралів, залежних від параметра, обчислити дані інтеграли. 1.
Означення визначеного інтеграла. Інтегральні суми
Нехай функція
Сукупність точок
Означення 1. Якщо існує скінченна границя інтегральної суми
Числа
Означення 2. Функція
Геометричний зміст визначеного інтеграла полягає в тому, що визначений інтеграл від невід’ємної та інтегровної на відрізку
Рис.1.1 Необхідною умовою існування визначеного інтеграла є обмеженість функції Достатньою умовою існування визначеного інтеграла є неперервність функції
Розглянемо деякі властивості визначеного інтеграла: 1) Визначений інтеграл не залежить від позначення змінної інтегрування:
2) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю:
3) Для будь-якого довільного сталого числа
4) При переставленні меж інтегрування визначений інтеграл змінює знак, тобто
5) Якщо функції
6) Якщо функція
7) Якщо функція
Аналогічно маємо, що
8) Якщо функції
9) Якщо функція
10) Якщо функція
11) Якщо функція
Це ствердження має назву теореми про середнє значення визначеного інтеграла.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 можна знайти, не використовуючи рекомендовану підстановку
можна знайти, не використовуючи рекомендовану підстановку  , а застосувавши штучний прийом:
, а застосувавши штучний прийом:
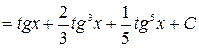 .
. , розкладаючи підінтегральну функцію на найпростіші дроби:
, розкладаючи підінтегральну функцію на найпростіші дроби: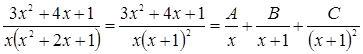 .
. є похідною знаменника
є похідною знаменника  , легко отримати:
, легко отримати:
 .
. є також елементарною функцією, говорять, що
є також елементарною функцією, говорять, що  «береться», тобто інтеграл виражається через елементарні функції (або інтеграл обчислюється). Якщо ж інтеграл не виражається через елементарні функції, то говорять, що інтеграл не «береться» (або «його знайти не можна»).
«береться», тобто інтеграл виражається через елементарні функції (або інтеграл обчислюється). Якщо ж інтеграл не виражається через елементарні функції, то говорять, що інтеграл не «береться» (або «його знайти не можна»). , оскільки не існує елементарної функції, похідна від якої б була рівна
, оскільки не існує елементарної функції, похідна від якої б була рівна  . Наведемо ще приклади інтегралів, що не «беруться», які мають велике значення в додатках:
. Наведемо ще приклади інтегралів, що не «беруться», які мають велике значення в додатках: - інтеграл Пуассона
- інтеграл Пуассона - інтегральний логарифм (теорія чисел)
- інтегральний логарифм (теорія чисел) - інтеграли Френеля (фізика)
- інтеграли Френеля (фізика) - інтегральні синус і косинус
- інтегральні синус і косинус - інтегральна показова функція.
- інтегральна показова функція. ,
,  ,
,  і інших добре вивчені, для них складені докладні таблиці значень для різних значень аргументу
і інших добре вивчені, для них складені докладні таблиці значень для різних значень аргументу  .
. визначена гама-функція
визначена гама-функція  . Мають місце наступні властивості гама-функції:
. Мають місце наступні властивості гама-функції: ,
, 
 визначена бета-функція
визначена бета-функція  . Має місце співвідношення:
. Має місце співвідношення: 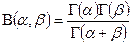 .
. задана на осі
задана на осі 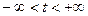 ; 2) кусково-гладка на кожному скінченному проміжку; 3)абсолютно інтегровна на осі
; 2) кусково-гладка на кожному скінченному проміжку; 3)абсолютно інтегровна на осі  , то у кожній точці неперервності вона може бути подана у вигляді інтегралу Фур’є (в дійсній формі):
, то у кожній точці неперервності вона може бути подана у вигляді інтегралу Фур’є (в дійсній формі): ,
, ,
,  .
. та початкову фазу
та початкову фазу  , то формула (4) набуває вигляду:
, то формула (4) набуває вигляду: .
. , де
, де  - частотна характеристика або спектр функції
- частотна характеристика або спектр функції  ,
,  - перетворення Фур’є функції
- перетворення Фур’є функції  2.
2. 
 визначена на відрізку
визначена на відрізку  ,
,  <
<  . Розіб’ємо відрізок
. Розіб’ємо відрізок  довільних частин так, щоб
довільних частин так, щоб <
< 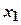 <
<  …<
…<  <
<  <
<  <…<
<…<  .
. назвемо
назвемо  -розбиттям відрізка
-розбиттям відрізка  та значення функції
та значення функції  у довільній точці
у довільній точці  . Позначимо через
. Позначимо через  - найбільшу довжину серед довжин частинних відрізків, тобто
- найбільшу довжину серед довжин частинних відрізків, тобто  . Утворимо суму
. Утворимо суму  , яка називається інтегральною сумою функції
, яка називається інтегральною сумою функції  на відрізку
на відрізку  .
. при умові, що найбільша із різниць
при умові, що найбільша із різниць  прямує до нуля, яка не залежить ані від способу розбиття відрізка
прямує до нуля, яка не залежить ані від способу розбиття відрізка  у кожному з частинних відрізків, то вона називається визначеним інтегралом функції
у кожному з частинних відрізків, то вона називається визначеним інтегралом функції  . Отже, згідно з означенням,
. Отже, згідно з означенням, .
. - підінтегральним виразом;
- підінтегральним виразом;  - змінною інтегрування, а відрізок
- змінною інтегрування, а відрізок  ,
, 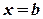 та віссю
та віссю  :
:
 .
. .
. справджується рівність:
справджується рівність: .
. .
. - інтегровні на відрізку
- інтегровні на відрізку  також є інтегровною на цьому відрізку, причому
також є інтегровною на цьому відрізку, причому .
. ,
,  , то вона інтегровна і в двох інших і для будь-якого взаємного розташування точок
, то вона інтегровна і в двох інших і для будь-якого взаємного розташування точок  має місце рівність
має місце рівність
 .
. <
<  і всюди на цьому відрізку
і всюди на цьому відрізку 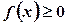 , то
, то .
. , якщо
, якщо  .
. , то
, то .
. також інтегровна на цьому відрізку, причому
також інтегровна на цьому відрізку, причому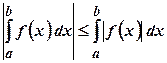 .
.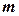 і
і  - відповідно її найменше і найбільше значення на цьому відрізку, то справджуються нерівності
- відповідно її найменше і найбільше значення на цьому відрізку, то справджуються нерівності .
. така, що виконується рівність:
така, що виконується рівність: .
.


