
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Границя функції. Обчислення границьСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай функція
виконується нерівність
Позначення:
Функція
виконується нерівність
Позначення:
Функція
При Функція Деякі властивості нескінченно малих величин:
1) якщо при 2) сума скінченого числа нескінченно малих величин є нескінченно малою величиною; 3) добуток обмеженої функції на нескінчену малу є нескінченно малою величиною; 4) частка від ділення нескінченно малої величини на функцію, яка має відміну від нуля границю, є нескінченно малою величиною. Якщо кожна з функцій 1) 2) 3) 4) При обчисленні границь часто використовують такі границі:
Число Число
Ліва і права границі функції називаються односторонніми границями.
Неперервність функції Функція 1) функція визначена в точці 2) існують скінчені односторонні границі функції 3) односторонні границі рівні між собою і дорівнюють значенню функції в точці Якщо не виконується хоча б одна з цих умов, то функція розриву функції. Якщо функція визначена в точці
Якщо хоча б одна із односторонніх границь не існує або дорівнює нескінченності, то розрив функції в точці р озривом другого роду, а точка Функція Всі елементарні функції неперевні в області свого визначення. Якщо функція 1) вона обмежена на цьому відрізку і досягає на ньому принаймні один раз свого найбільшого і найменшого значення; 2) набуває всіх проміжних значень між найменшим і найбільшим значеннями; 2) при зміні знаку функції на відрізку знайдеться принаймні одна точка
I.Довести, що функція 1. 2. 3. 4. II. Дослідіть на неперервність наступні функції в точці 1. 2. 3. 4. 5. 6. 7. 8. III. Обчислити границю: 1. 3. IV. Знайти область визначення функції: 1. 3. 5. 7. V. Які із функцій є парними, які непарними: 1. VI. Обчислити границю: 1.
3. 5. 7. 9. 11. 13. 15. 17. 19. 21.
23. Глава 4. Диференціальне числення функції однієї змінної Означення похідної. Рівняння дотичної. Рівняння нормалі Похідна Похідною функції
де Позначається похідна через
Значення похідної функції З погляду фізики похідна має таке тлумачення: а) швидкість руху б) лінійна густина в) сила струму г) теплоємність
Односторонні похідні позначаються відповідно так: Ліва похідна Права похідна Якщо обидві ці границі існують і рівні між собою, то тільки в цьому випадку кажуть, що в цій точці існує похідна:
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.50.1 (0.009 с.) |

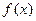 визначена в деякому околі Х точки
визначена в деякому околі Х точки  , крім, можливо, самої точки
, крім, можливо, самої точки 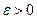 існує число
існує число 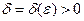 таке, що для всіх
таке, що для всіх 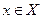 , які задовольняють нерівність
, які задовольняють нерівність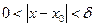 ,
,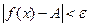 .
. .
.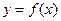 при
при 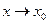 є нескінченно великою (має границю
є нескінченно великою (має границю 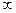 ), якщо вона визначена в деякому околі точки
), якщо вона визначена в деякому околі точки 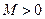 існує таке
існує таке 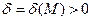 , що для всіх
, що для всіх  , які задовольняють нерівність
, які задовольняють нерівність 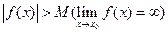 .
.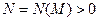 , що для всіх
, що для всіх 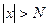 , виконується нерівність
, виконується нерівність 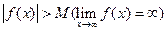 .
.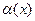 є нескінченно великою при
є нескінченно великою при  ), якщо
), якщо 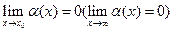 .
.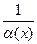 і
і 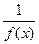 - відповідно нескінченно велика і нескінченно мала велечини;
- відповідно нескінченно велика і нескінченно мала велечини;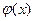 має скінчену границю при
має скінчену границю при 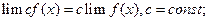
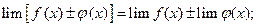

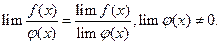
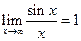 - перша важлива границя;
- перша важлива границя;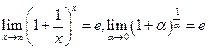 - друга важлива границя.
- друга важлива границя.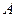 є границею функції
є границею функції 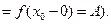
 є границею функції
є границею функції 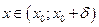 виконується нерівність
виконується нерівність
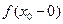 і
і 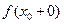 ;
;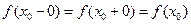 .
. рівні між собою, то розрив функції в точці
рівні між собою, то розрив функції в точці  є стрибком функції. Зокрема, якщо
є стрибком функції. Зокрема, якщо 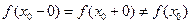 , то розрив у точці
, то розрив у точці 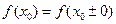 , дістанемо непервну функцію.
, дістанемо непервну функцію.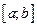 , якщо вона непервна в кожній внутрішній точці цього вірізка, а також у точці
, якщо вона непервна в кожній внутрішній точці цього вірізка, а також у точці 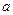 справа і в точці
справа і в точці 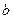 зліва.
зліва. , в якій
, в якій  .
. ;
; ;
;
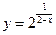 в т.
в т. 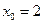 ;
;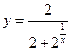 в т.
в т. 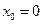 ;
;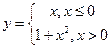 в т.
в т. 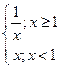 в т.
в т.  ;
;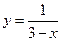 в т.
в т. 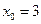 ;
;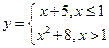 в т.
в т.  в т.
в т. 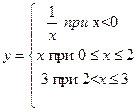 в т.
в т.  ; 2.
; 2. 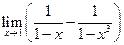 ;
;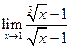 ; 4.
; 4. 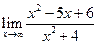 .
.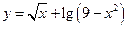 ; 2.
; 2. 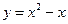 ;
;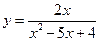 ; 4.
; 4. 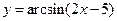 ;
;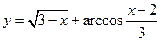 ; 6.
; 6. 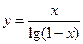 ;
; ; 8.
; 8. 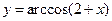 .
.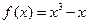 ; 2.
; 2. 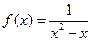 .
. ; 2.
; 2. 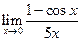 ;
;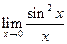 ; 4.
; 4. 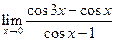 ;
;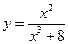 ; 6.
; 6. 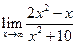 ;
;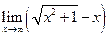 ; 8.
; 8. 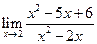 ; 10.
; 10. 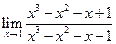 ;
;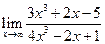 ; 12.
; 12.  ;
;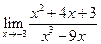 ; 14.
; 14.  ;
;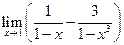 ; 16.
; 16. 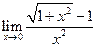 ; 18.
; 18.  ;
; ; 20.
; 20. 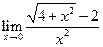 ;
;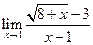 ; 22.
; 22. 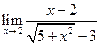 ;
;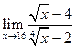 ; 24.
; 24.  .
.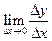 ,
,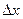 - приріст аргументу, а
- приріст аргументу, а 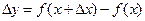 - приріст функції.
- приріст функції.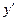 , або
, або  , або
, або 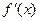 . Отже,
. Отже,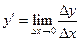 , або
, або 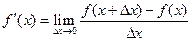 .
. дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою
дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою 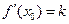 .
.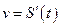 , де
, де 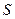 - шлях,
- шлях,  - час;
- час;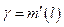 , де
, де 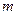 - маса стержня,
- маса стержня,  - довжина;
- довжина;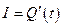 , де
, де 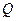 – кількість електрики, що проходить через провідник,
– кількість електрики, що проходить через провідник,  , де
, де 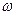 – кількість теплоти;
– кількість теплоти;  ;
;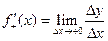 .
.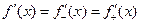 .
. 


