
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знакододатні ряди. Достатні ознаки збіжностіСодержание книги Поиск на нашем сайте
Ознака порівняння. Нехай ряди Гранична ознака порівняння. Нехай ряди Ознака Д’Аламбера. Якщо для знакододатного ряду
Ознака Коші. Якщо для знакододатного ряду Інтегральна ознака Коші. Нехай задано ряд
причому І. Дослідити на збіжність ряди (ознака Д’Аламбера): 1. 2. 3. 4.
5.
ІІ. Дослідити на збіжність ряди (ознака Коші): 1. 2. 3. 8. Степеневі ряди Теорема Абеля. Інтеграл та радіус збіжності степеневого ряду Поняття степеневого ряду. Теорема Абеля Функціональний ряд виду Теорема Абеля. Якщо степеневий ряд
Для визначення радіуса та інтервалу збіжності степеневого ряду, складемо ряд з модулів членів ряду тобто Припустимо, що для коефіцієнтів степеневого ряду існує границя
Число Радіус збіжності
Знайти область збіжності степеневих рядів: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Ряд Тейлора. Розкладання елементарних функцій у ряд Маклорена Розвинення елементарних функцій у ряди Тейлора і Маклорена. Наближені обчислення Ряд Тейлора має вигляд:
При
Розвинення деяких функцій у ряд Маклорена:
І. Розкласти в ряд Маклорена функції:
1. 2. 3. 4. 5. 6. 7.
ІІ. Скласти ряд Тейлора для даних функцій у вказаних точках: 1. 2.
Ряди Фур’є Тригонометричні ряди Нехай
де
Якщо функція
де
Якщо функція
де
Для довільної інтегрованої
де Нехай функція
де
Якщо функція
де
а якщо
де
Ортогональність системи функцій Система функцій Система функцій І. Розкласти в ряд Фур’є функцію: 1. 2. 3. 4. ІІ. Які із цих систем функцій є ортогональними на відрізку
1. 2. 3. 4.
Відповіді Глава 3. §3.1 II. а)
III. 1. -1; 2.
§3.2 III. 1. IV. 1. 4. 7. V. 1. непарна. 2. ні, парна, ні, непарна. VI. 1. непарна. 2. ні, парна, ні, непарна. VI. 1. 3. 0. 4.
Глава 4. §4.1 2. рівняння дотичної: 6.
§4.2 I. 1. 4. 5. 6. 8. 9. 10. 13. 15.
II.1. 2. 2. 0. 3. 4. 4. 1. 5. 2. 6.
§4.3 I. 1. функція зростає на інтервалі
II.1. 2. 4.
III.1. 2.
VI. 1. 2. 3.
VI.
§4. I. 1.
І1. 4. III. 1.
Глава 5. §5.1 1. 3. 6. 12. 14. 16. 18. 19.
20. 22. 23. 26. 27. 30.
§5.2 1. 26. 2. 1. 3. 6. 18. 24. 29.
§5.3 I. 1. 6. 9.
II. 1. 16. 2. 6. 3. 36. 4. Глава 6. §6.1 VI. 1. 2.
§6.2 I. 1. 2. 3. 4. 5. 7. 10. 11. 12. 13.
17.
II.
III.
Глава 7 §7.1 VI. 1. §7.2 I. 1. 4. II. 1. III. 1. IV. 5. V. 1. VI. 4. §7.3 I. 1. 4. II. 1. III. 4. IV. 1. V. 3. §7.4 I. 1. 3. 6. 9. II. 1. 3. 6. Глава 8 §8.1 I. 1. розбіжний. 2. збіжний. 3. розбіжний. 1. розбіжний. 2. розбіжний. 3. збіжний. 4. збіжний. 5. розбіжний. 1. збіжний. 2. збіжний. 3. збіжний. 4. збіжний. 5. збіжний. §8.2 I. 1. збіжний. 2. розбіжний. 3. збіжний. 4. збіжний. 5. розбіжний. 6. збіжний. 7. збіжний. 8. збіжний. 9. збіжний. 10. збіжний. 1. збіжний. 2. збіжний. 3. розбіжний. 4. розбіжний. 5. збіжний. 6. збіжний. 7. розбіжний. §8.3 1. 4. I. 1. 2. 3. 6.
II. 1. 2. §8.5 І. 2. 3. 4.
II. 1. неортогональна. 2. ортогональна. 3. ортогональна. 4. ортогональна. Список рекомендованої літератури Основна: 1. Дубовик В. П., Юрик І. І. Вища математика. Збірник задач:- 2. Дубовик В. П., Юрик 1. І. Вища математика: Навч. посіб. - К.: 3. Дюженкова Л. І., Дюженкова О. Ю., Михалін Г. О. Вища" 4. Лейфура В. М. та ін. Математика: підручник для студентів 5. Соколенко О. І. Вища математика. Підручник. - К.: Видав Додаткова: 1. Беклемишев Д. В. Курс аналитической геометрии и линейной 2. Дискант В. І., Береза Л. Р., Грижук О. П., Захаренко Л. М. 3. Завало С. Т. Курс алгебри. - К.: Вища школа. Головне 4. Пастушенко С. М., Підченко Ю. П. Вища математика. Довідник 5. Щипачев В. С. Задачник по высшей математике. Учебник
6. Щипачев В. С. Курс высшей математики. Учебник / Под
ПРО АВТОРА Кацімон Оксана Василівна – викладач циклової комісії фундаментальних дисциплін Черкаського державного бізнес-коледжу. Закінчила Черкаський педагогічний інститут ім. Б. Хмельницького в 1993 р. Викладає математику з 1993 року. Спеціаліст вищої категорії. Автор навчально-методичного видання “Вища математика. Методичні рекомендації”(2002р.) та “Вища математика. Збірник задач” (2005р.).
Навчальне видання Кацімон Оксана Василівна
ВИЩА МАТЕМАТИКА Збірник задач ІІ частина
Редактор Н. А. Азьмук Комп’ютерний набір О. В. Кацімон Коректор В.Л. Красюк
Підписано до друку. Формат 60х84 1/16 Папір офсетний. Гарнітура Times New Roman. Друк офсетний. Умов. друк. арк. 0,87 Тираж 80 прим. Зам. № 187 Видавництво ТОВ "Інтеграл-техноімпекс" 18000, м.Черкаси, вул. Смілянська, 2 За довідками з питань реалізації звертатись за тел. (0472) 64-05-15
|
|||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.128.81 (0.009 с.) |

 та
та  знакододатні і
знакододатні і  ,
,  тоді якщо ряд
тоді якщо ряд 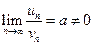 , тоді ряди або одночасно збіжні, або одночасно розбіжні.
, тоді ряди або одночасно збіжні, або одночасно розбіжні.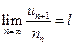 , то ряд збіжний при
, то ряд збіжний при  і розбіжний при
і розбіжний при  .
.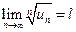 , то ряд збіжний при
, то ряд збіжний при  ,
,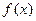 додатна, неперервна і монотонно спадна функція на проміжку
додатна, неперервна і монотонно спадна функція на проміжку  . Тоді ряд
. Тоді ряд  збіжний, якщо збіжний невласний інтеграл
збіжний, якщо збіжний невласний інтеграл  , і розбіжний, якщо цей інтеграл розбіжний.
, і розбіжний, якщо цей інтеграл розбіжний. 6.
6. 
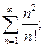 7.
7. 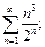
 8.
8. 
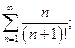 9.
9. 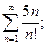
 10.
10. 
 5.
5. 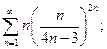
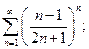 6.
6. 
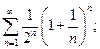 7.
7. 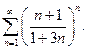
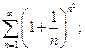
 називають степеневим рядом.
називають степеневим рядом. , то він абсолютно збіжний для всіх значень
, то він абсолютно збіжний для всіх значень  , що задовольняють нерівність
, що задовольняють нерівність  . Якщо при
. Якщо при 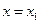 ряд
ряд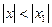 .
. .
.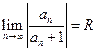 або
або  .
. називається радіусом збіжності степеневого ряду, а інтервал
називається радіусом збіжності степеневого ряду, а інтервал  - його інтервалом збіжності. Питання збіжності ряду при
- його інтервалом збіжності. Питання збіжності ряду при  розв’язується для кожного ряду окремо. Якщо
розв’язується для кожного ряду окремо. Якщо  , то ряд є збіжним на всій числовій осі, а при
, то ряд є збіжним на всій числовій осі, а при  ряд збігається лише в точці
ряд збігається лише в точці  .
. визначається за тими самими формулами, що й ряд
визначається за тими самими формулами, що й ряд  , тобто він має вигляд
, тобто він має вигляд  .
.
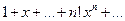
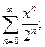
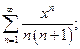





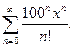


 маємо ряд Маклорена
маємо ряд Маклорена
 ,
, 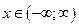 ;
; ,
,  ,
, 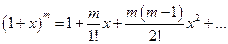
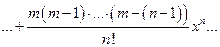 ,
,  ;
; ,
,  ,
,  ;
; ,
,  ;
;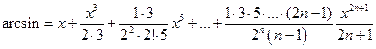 ,
, ,
, 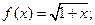


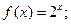
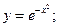


 ,
, 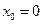 ,
,  ;
; ,
,  ,
,  .
. - періодична кусково-диференційована на відрізку
- періодична кусково-диференційована на відрізку  функція. Тоді ряд Фур’є цієї функції має вигляд
функція. Тоді ряд Фур’є цієї функції має вигляд ,
, ;
;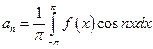 ;
;  .
. парна на
парна на  ,
, ;
;  .
. ,
,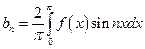 .
.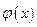 виконується рівність
виконується рівність ,
,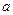 - довільне число.
- довільне число. , має період
, має період  і на відрізку
і на відрізку  ,
, ,
,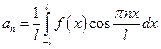 ,
,  .
.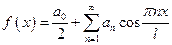 ,
,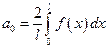 ,
,  .
. ,
, .
. ортогональна на
ортогональна на 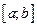 , якщо
, якщо 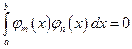
 .
. , якщо
, якщо 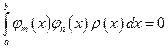
 на відрізку
на відрізку 
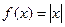 на відрізку
на відрізку  ,
,  ;
;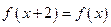 ,
,  .
. :
: ,
,  ,
, 
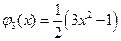 ,
, 
 ,
, 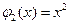 ;
; ,
, 
 б)
б) 
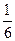 . 3.
. 3.  . 4. 3. 5.
. 4. 3. 5. 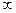 . 6.
. 6. 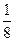 . 2. -1. 3.
. 2. -1. 3. 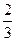 . 4. 1.
. 4. 1.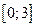 . 2.
. 2.  . 3.
. 3. 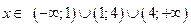 .
.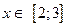 . 5.
. 5.  . 6.
. 6.  .
.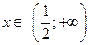 . 8.
. 8.  .
. . 2. 0.
. 2. 0. .
. ; рівняння нормалі:
; рівняння нормалі:  . 3. рівняння дотичної:
. 3. рівняння дотичної:  ; рівняння нормалі:
; рівняння нормалі:  . 4. а) рівняння дотичної:
. 4. а) рівняння дотичної:  ; рівняння нормалі:
; рівняння нормалі:  . б) рівняння дотичної:
. б) рівняння дотичної:  ; рівняння нормалі:
; рівняння нормалі:  . 5. т.
. 5. т.  .
. . 7. а)
. 7. а)  ; в)
; в) 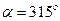 .
. . 2.
. 2.  . 3.
. 3.  .
. .
. .
. . 7.
. 7.  .
. .
.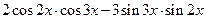 .
. . 11.
. 11.  . 12.
. 12.  .
.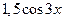 . 14.
. 14.  .
.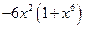 .
. . 7.
. 7.  . 8. 0. 9. 0.
. 8. 0. 9. 0.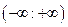 . 2.
. 2.  - функція спадає,
- функція спадає, 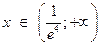 - функція зростає. 3.
- функція зростає. 3.  - функція спадає,
- функція спадає,  - функція зростає. 4.
- функція зростає. 4.  - функція зростає;
- функція зростає;  - функція спадає. 5.
- функція спадає. 5.  - функція спадає;
- функція спадає;  функція зростає. 6.
функція зростає. 6.  - функція спадає
- функція спадає  функція зростає.
функція зростає. ,
,  .
.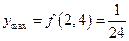 . 3. Функція зростає на множині дійсних чисел.
. 3. Функція зростає на множині дійсних чисел. ,
,  . 5.
. 5.  ,
,  ,
,  .
. ,
,  .
. ,
,  .
.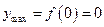 ,
,  .
.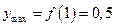 ,
,  .
. . 4.
. 4.  ,
,  .
. .
.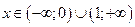 - крива вгнута,
- крива вгнута,  - крива опукла. 2.
- крива опукла. 2.  - крива опукла,
- крива опукла,  - крива вгнута. 3.
- крива вгнута. 3.  - крива опукла,
- крива опукла,  - крива вгнута. 4.
- крива вгнута. 4.  - крива опукла,
- крива опукла,  - крива вгнута. 5.
- крива вгнута. 5.  - крива вгнута,
- крива вгнута,  - крива опукла. 6. крива вгнута на множині дійсних чисел.
- крива опукла. 6. крива вгнута на множині дійсних чисел. . 2.
. 2. 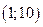 . 3.
. 3.  ,
,  ,
,  .
.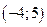 . 5.
. 5.  . 6.
. 6.  - похила асимптота. 2.
- похила асимптота. 2.  - горизонтальна асимптота. 3.
- горизонтальна асимптота. 3.  - похила асимптота. 4.
- похила асимптота. 4.  - вертикальна асимптота. 5.
- вертикальна асимптота. 5.  - горизонтальна асимптота.
- горизонтальна асимптота. . 2.
. 2.  .
.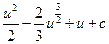 . 4.
. 4.  . 5.
. 5.  .
. . 7.
. 7. 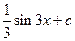 . 8.
. 8.  . 9.
. 9. 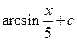 . 10.
. 10.  . 11.
. 11.  .
. . 13.
. 13. 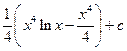 .
.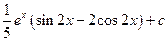 . 15.
. 15.  .
. . 17.
. 17.  .
. .
.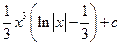 .
. . 21.
. 21.  .
. .
.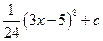 . 24.
. 24.  . 25.
. 25.  .
.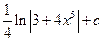 .
. . 28.
. 28.  . 29.
. 29. 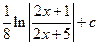 .
. .
. . 4.
. 4.  . 5.
. 5. 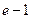 .
. . 7.
. 7.  . 8.
. 8.  . 9. 61. 10.
. 9. 61. 10.  . 12.
. 12. 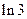 . 13.
. 13.  . 14.
. 14.  . 15.
. 15. 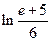 . 16.
. 16. 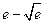 . 17.
. 17.  . 22.
. 22. 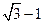 . 23.
. 23.  .
.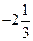 . 27.
. 27.  . 28. 12.
. 28. 12. . 30.
. 30.  .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 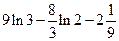 .
. . 7. 2. 8.
. 7. 2. 8.  .
. . 10.
. 10. 
 . 8. 6. 9.
. 8. 6. 9. 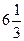 . 10. 6
. 10. 6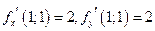 .
. .
. .
. .
.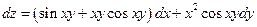 .
. .
. . 6.
. 6.  .
. . 8.
. 8.  . 9.
. 9. 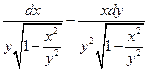 .
. .
. .
. .
. .
. . 18.
. 18.  .
. .
.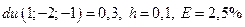 .
. . 2.
. 2.  .
. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  .
.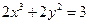 . 2.
. 2.  . 3.
. 3. 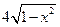 . 4.
. 4.  . 5.
. 5. 
 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
.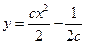 .
. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  .
. . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5. 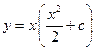 .
. . 2.
. 2.  . 3.
. 3. 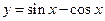 .
.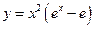 . 5.
. 5. 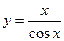
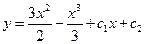 . 2.
. 2.  .
. . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  .
. . 2.
. 2.  .
. . 4.
. 4. 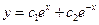 . 5.
. 5. 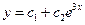 .
. . 7.
. 7.  . 8.
. 8.  .
. . 10.
. 10.  .
. . 2.
. 2.  .
. . 4.
. 4.  . 5.
. 5.  .
. .
. . 2. ряд збіжний лише в точці
. 2. ряд збіжний лише в точці 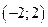 .
. . 5.
. 5.  . 6.
. 6. 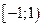 . 7. ряд абсолютно збіжний по всій числовій вісі. 8.
. 7. ряд абсолютно збіжний по всій числовій вісі. 8.  . 10.
. 10.  .
. .
. .
.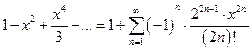 . 4.
. 4.  .
. . 7.
. 7.  .
.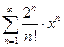 , при
, при  , при
, при 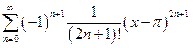 , при
, при  , при
, при  .
.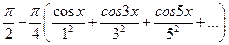 .
. ,
, .
.


