
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повний диференціал функції та його застосування до обчислення значень функцій та похибокСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функція
де
де Аналогічна формула вірна для диференційованої функції трьох змінних
Для наближеного обчислення значення функції, наприклад, двох змінних користуються наближеною рівністю
Максимальна абсолютна похибка
де Максимальну відносну похибку за формулою І. Знайти повний диференціал функцій: 1. 3. 5. 7. 9. 11. 13. 15. 17.
ІІ. Знайти значення повного диференціала функції:
ІІІ. Знайти повний диференціал функції VІ. Обчислити наближено: 1. 2.
3. 4. 5. 6. 7.
Глава 7. Диференціальні рівняння Диференціальні рівняння першого порядку. Задача Коші. Загальний і частинний розв’язок диференціального рівняння першого порядку Загальні поняття та означення. Геометричний зміст диференціального рівняння Диференціальним рівнянням першого порядку називається рівняння виду
яке пов’язує незалежну змінну Розв’язком диференціального рівняння (1) на деякому інтервалі перетворює його в тотожність по Функція 1) функція 2) для довільної точки
Частинним розв’язком рівняння (1) називається функція
Якщо загальний розв’язок диференціального рівняння знайдено в неявному вигляді, тобто у вигляді рівняння
І. Перевірити, чи є розв’язками даних диференціальних рівнянь указані функції. 1. 2. 3. 4. 5. 6.
ІІ. Довести, що для даних диференціальних рівнянь указані функції є розв’язком при будь-якому значенні 1. 2.
ІІІ. Чи є слідуючі функції а) 1. b) c) розв’зком рівнянь: 1. ІV. Знайти значення 1.
2.
Диференціальні рівняння першого порядку з відокремлюваними змінними. Однорідні диференціальні рівняння першого порядку
7.2.1 Диференціальні рівняння першого порядку з відокремлюваними змінними
Рівняння виду
де Рівняння виду
називається диференціальним рівнянням з відокремленими змінними. Загальний інтеграл диференціального рівняння (2) має вигляд
Диференціальне рівняння (1) є окремим випадком рівняння виду
Для відокремлення змінних у цьому рівнянні досить обидві його частини поділити на функцію
Однорідні диференціальні рівняння Функція
Диференціальне рівняння
називається однорідним, якщо функція * є однорідною функцією нульового виміру. Підстановкою
де
Рівняння виду
де змінною
І. Знайти загальний розв’язок рівняння: 1. 2. 3. 4. 5. ІІ. Знайти частинні розв’язки рівнянь: 1. 2. 3. 4. 5. ІІІ. Розв’язати рівняння: 1. 2. 3. 4. 5. ІV. Знайти частинні розв’язки рівнянь: 1. 2. 3. 4.
5. Лінійні диференціальні рівняння першого порядку. Диференціальні рівняння вищих порядків
|
||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 864; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.190.187 (0.009 с.) |

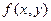 називається диференційованою в точці
називається диференційованою в точці  , якщо її повний приріст
, якщо її повний приріст  можна подати у вигляді
можна подати у вигляді ,
,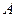 та
та  – дійсні числа, що не залежать від
– дійсні числа, що не залежать від 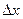 та
та  ,
,  і
і 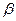 - нескінченно малі при
- нескінченно малі при  і
і  функції. Повним диференціалом
функції. Повним диференціалом  функції
функції  називається головна лінійна частина приросту функції, яка обчислюється за формулою
називається головна лінійна частина приросту функції, яка обчислюється за формулою ,
, ,
,  .
.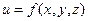 :
: .
. .
. змінної
змінної  обчислюється за формулою
обчислюється за формулою ,
, - максимальна абсолютна похибка змінної
- максимальна абсолютна похибка змінної  .
. зручно оцінювати
зручно оцінювати .
. ; 2.
; 2. 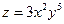 ;
; ; 4.
; 4.  ;
; ; 6.
; 6. 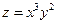 ;
; ; 8.
; 8.  ;
; ; 10.
; 10. 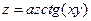
 ; 12.
; 12.  .
. . 14.
. 14.  .
. . 16.
. 16.  .
. . 18.
. 18.  .
. , при
, при  ,
,  ,
,  ,
, 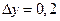 .
. , обчислити його значення при
, обчислити його значення при  ,
,  ,
,  ,
,  . Знайти абсолютну і відносну похибку наближення:
. Знайти абсолютну і відносну похибку наближення:  і
і  .
. .
. .
. .
.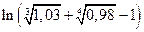 .
. .
. .
. .
. , (1)
, (1) , невідому функцію
, невідому функцію  називається диференційована на цьому інтервалі функція
називається диференційована на цьому інтервалі функція  , яка при підстановці в рівняння (1)
, яка при підстановці в рівняння (1) , яка залежить від аргументу і довільної сталої
, яка залежить від аргументу і довільної сталої  , називається загальним розв’язком рівняння(1) в області
, називається загальним розв’язком рівняння(1) в області  , якщо вона задовольняє дві умови:
, якщо вона задовольняє дві умови: є розв’язком рівняння при будь-якому значенні сталої
є розв’язком рівняння при будь-якому значенні сталої  можна знайти таке значення
можна знайти таке значення  , що функція
, що функція  задовольняє початкову умову:
задовольняє початкову умову: .
.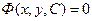 , то такий розв’язок називають загальним інтегралом диференціального рівняння (1). Рівність
, то такий розв’язок називають загальним інтегралом диференціального рівняння (1). Рівність  називають частинним інтегралом рівняння.
називають частинним інтегралом рівняння. :
: ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
;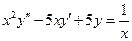 ,
,  ;
; ,
,  .
. , і знайти частинні розв’язки, що задовольняють початковим умовам:
, і знайти частинні розв’язки, що задовольняють початковим умовам: ,
,  ,
,  .
. ,
,  ,
,  .
. ; a)
; a)  ;
; ; 2. b)
; 2. b)  ;
; ; c)
; c)  .
. . 2.
. 2.  .
.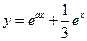 ,
, 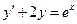 ;
; ,
,  .
. , (1)
, (1)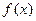 і
і  - задані і неперервні на деякому інтервалі функції, називається диференціальним рівнянням з відокремлюваними змінними.
- задані і неперервні на деякому інтервалі функції, називається диференціальним рівнянням з відокремлюваними змінними.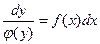
 (2)
(2) .
. .
. . При цьому втрачаємо розв’язки
. При цьому втрачаємо розв’язки  ,
,  .
. -го виміру відносно змінних
-го виміру відносно змінних  , якщо для довільного
, якщо для довільного  виконується тотожність
виконується тотожність . (1)
. (1) (2)
(2) ,
, 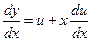 ,
,  ,
, - невідома функція, рівняння (2) зводиться до рівняння з відокремленими змінними
- невідома функція, рівняння (2) зводиться до рівняння з відокремленими змінними .
. ,
, ,
,  ,
,  ,
, 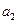 ,
, 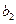 ,
,  - задані сталі, зводиться до однорідного рівняння
- задані сталі, зводиться до однорідного рівняння ,
,  , якщо
, якщо  . Числа
. Числа 
 ;
; ;
; ;
; ;
; .
. , якщо
, якщо  , при
, при  ;
; , якщо
, якщо  , при
, при  ;
; , якщо
, якщо  , якщо
, якщо  ;
; ;
; ;
; ;
; ;
; , якщо
, якщо 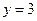 , при
, при  , якщо
, якщо  , якщо
, якщо  , якщо
, якщо  , якщо
, якщо 


