
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування диференціальних рівняньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
За допомогою степеневих рядів
Для наближеного інтегрування диференціальних рівнянь розв’язок відповідної задачі Коші розшукують у вигляді розвинення в степеневий ряд в околі початкової точки Якщо диференціальне рівняння є лінійним, застосовується також метод невизначених коефіцієнтів, який дозволяє побудувати низку рекурентних формул, а іноді навіть знайти правило для обчислення будь-якого коефіцієнта ряду.
Зразки розв’язування задач 1.Знайти перші три ненульові члени розвинення у степеневий ряд розв’язку задачі Коші
Запишемо шукане розвинення у степеневий ряд в околі початкової точки
Обчислимо за допомогою диференціального рівняння значення декількох похідних шуканої функції.
Тоді
2.Знайти перші три ненульові члени розвинення у степеневий ряд розв’язку задачі Коші
Запишемо шукане розвинення у степеневий ряд в околі початкової точки
Обчислимо за допомогою диференціального рівняння значення декількох похідних шуканої функції.
Тоді
3. Знайти перші три ненульові члени розвинення у степеневий ряд розв’язку задачі Коші
Запишемо шукане розвинення у степеневий ряд в околі початкової точки
Обчислимо за допомогою диференціального рівняння значення декількох похідних шуканої функції.
Тоді
4.Знайти розвинення у степеневий ряд розв’язку задачі Коші
Запишемо шукане розвинення у вигляді ряду з невизначеними коефіцієнтами, знайдемо його похідні та підставимо ці ряди у диференціальне рівняння та початкові умови (права частина рівняння також повинна бути записаною у вигляді ряду).
Порівняємо коефіцієнти при однакових степенях змінної
Можна довести, що коефіцієнти ряду задаються залежностями
Тоді шуканий ряд має вигляд
Легко помітити, що отриманий розв’язок може бути записаний у вигляді
5.Знайти розвинення у степеневий ряд розв’язку задачі Коші
Запишемо шукане розвинення, знайдемо його похідні та підставимо отримані ряди у диференціальне рівняння та початкові умови.
Отримаємо рекурентну послідовність рівностей
Можна довести, що коефіцієнти ряду задаються залежностями
Тоді шуканий ряд має вигляд
Легко помітити, що отриманий розв’язок може бути записаний у вигляді
Завдання для самостійної роботи
Знайти перші три ненульові члени розвинення у степеневий ряд розв’язку задачі Коші
1. 2. Знайти розвинення у степеневий ряд розв’язку задачі Коші 3. 4. Відповіді 1. 2. 3. 4.
Розділ 4 РЯДИ ФУР’Є
Основні формули Основні формули, за якими будуються розвинення в ряд Фур’є функцій та обчислюються коефіцієнти цих розвинень, наведені у вигляді таблиці.
У процесі обчислення коефіцієнтів Фур’є часто застосовуються деякі відомі математичні формули та факти. Наведемо їх.
Формули перетворення добутків тригонометричних формул в суму
Важливі властивості тригонометричних функцій
Деякі формули інтегрування
4.2.Розвинення в ряди Фур’є 2π-періодичних функцій
Розглянемо деяку 2π -періодичну функцію Функціональний ряд виду
називається рядом Фур’є функції
Якщо 2π -періодична функція f(x) є парною (
де
Непарна 2π - періодична функція f(x) розкладається в ряд Фур’є тільки за синусами:
де
Зразки розв’язування задач
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 697; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.009 с.) |

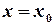 , тобто будують ряд Тейлора або Маклорена, коефіцієнти якого обчислюють шляхом диференціювання.
, тобто будують ряд Тейлора або Маклорена, коефіцієнти якого обчислюють шляхом диференціювання. ,
,  .
.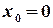 , тобто ряд Маклорена для функції
, тобто ряд Маклорена для функції 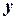 :
: .
. ;
; ,
,
 ;
; ,
, ;
; ,
,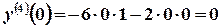 ;
; ,
, ;
;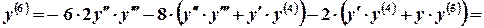
 ,
, ;
;
 ,
,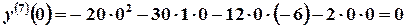 ;
;

 ,
, .
. ,
, .
. ,
,  .
. , тобто ряд Тейлора для функції
, тобто ряд Тейлора для функції  .
.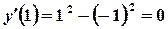 ;
; ,
, ;
; ,
, .
.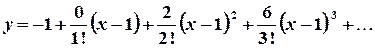 ,
,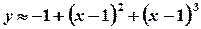 .
.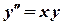 ,
, 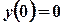 ,
,  .
. ;
; ;
; ;
; ;
; ;
;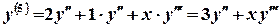 ;
; ;
; ;
;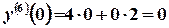 ;
; ;
;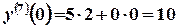 .
. ,
,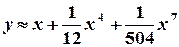 .
. ,
,  .
. ,
, ,
, ,
, .
. ;
; ;
;
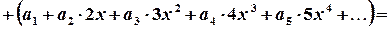
 ,
,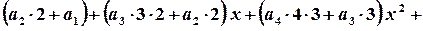

 та отримаємо рекурентну послідовність рівностей:
та отримаємо рекурентну послідовність рівностей: ;
; ;
;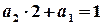 ,
, 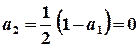 ;
;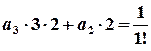 ,
,  ;
; ,
,  ;
; ,
,  ;
;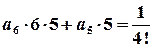 ,
,  ;
; 
 ,
, 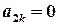 .
. .
. , де
, де  .
. ,
,  ,
,  .
. ;
;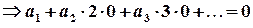 ;
;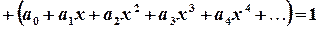 ,
,
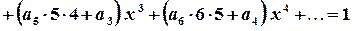 .
.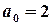 ;
; ;
; ,
,  ;
;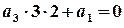 ,
,  ;
;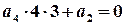 ,
, 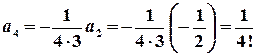 ;
; ,
,  ;
; ,
,  ;
;  ,
,  .
. .
. .
. ,
, 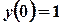 .
. ,
,  ,
,  ,
, 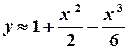 .
. .
.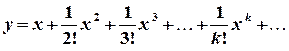 ;
;  .
. ;
; 
 ;
; 
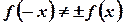
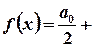


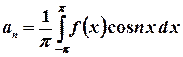
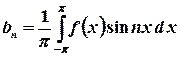




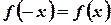




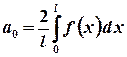




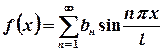




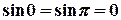

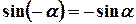


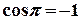

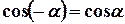




 , неперервну, або таку, що на відрізку
, неперервну, або таку, що на відрізку  має скінчене число точок розриву першого роду.
має скінчене число точок розриву першого роду.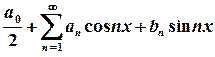 , коефіцієнти якого обчислюються за формулами
, коефіцієнти якого обчислюються за формулами ,
, ,
,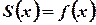 , а в точках розриву сума ряду дорівнює півсумі лівосторонньої та правосторонньої границь функції
, а в точках розриву сума ряду дорівнює півсумі лівосторонньої та правосторонньої границь функції  .
.
 .
.


