
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З’ясувати за допомогою ознак збіжності, чи буде збіжним числовий ряд.Содержание книги
Поиск на нашем сайте
6. Загальний член ряду задається формулою
7. Степінь числівника
8.
9. Загальний член ряду є правильною дробово-раціональною функцією (степінь числівника менший за степінь знаменника), числівник еквівалентний величині Порівняємо досліджуваний ряд з розбіжним гармонійним рядом
Згідно з граничною ознакою порівняння досліджуваний ряд
10. Скористаємося граничною ознакою порівняння. Оберемо допоміжний ряд.
Таким чином, Порівняємо досліджуваний ряд з узагальненим гармонійним рядом
Згідно з граничною ознакою порівняння ряд
11. Загальний член ряду містить арксинус нескінченно малого аргументу, отже, за допомогою граничної ознаки порівняння можна щонайменше позбутися оберненої тригонометричної функції. Скористаємося наслідком першої важливої границі
Порівняємо досліджуваний ряд з узагальненим гармонійним рядом
Згідно з граничною ознакою порівняння досліджуваний ряд
12. Скористаємося тим, що для досить великих значень змінної логарифм степеневої функції буде меншим за будь-який додатний степінь.
Ряд
13. Скористаємося тим, що для досить великих значень змінної логарифм степеневої функції буде більшим за одиницю.
Ряд Зауваження. Якщо логарифмічна функція розташована у знаменнику, для її оцінювання доцільно скористатися нерівністю
14. До загального члена ряду входить показникова функція, отже, можна використати признак Даламбера.
За ознакою Даламбера ряд збігається.
15. Побудуємо формулу загального члена ряду. Числівники дробів є факторіалами чисел
За ознакою Даламбера ряд розбігається.
16. Загальний член ряду є арктангенсом нескінченно малого аргументу, який містить факторіал, отже, скористаємося ознакою Даламбера.
При обчисленні
За ознакою Даламбера ряд збігається.
17. Спроба використати ознаку Даламбера для дослідження наданого ряду призведе до результату
Помітимо, що кожен з множників буде більшим за одиницю, отже, справджується нерівність Ряд
18. Як і у попередньому прикладі, ознака Даламбера призведе до результату
Легко помітити, що кожний з множників Тоді
19. Загальний член ряду є степенево-показниковою функцією, отже, можна спробувати радикальну ознаку Коші.
За радикальною ознакою Коші ряд розбігається.
20. Скористаємося радикальною ознакою Коші.
За радикальною ознакою Коші ряд збігається. 21. Скористаємося радикальною ознакою Коші. При обчисленні
За радикальною ознакою Коші ряд збігається.
22. Спроба використати радикальну ознаку Коші призведе до результату
Ряд розбігається.
23. Загальний член ряду задається за допомогою функції
Інтеграл є розбіжним, отже, ряд також розбігається.
Завдання для самостійної роботи
З’ясувати за допомогою означення, чи буде збіжним числовий ряд, та за умови позитивної відповіді знайти суму ряду.
1. З’ясувати за допомогою ознак збіжності, чи буде збіжним числовий ряд.
4. 7. 10. 13. 16. 18. 21. 24. 27. 29. 32. 34.
Відповіді. 1. Розбігається. 2. Збігається,
Знакозмінні ряди
Якщо серед членів ряду є як додатні, так і від’ємні, такий ряд називається знакозмінним. Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд, складений з абсолютних величин його членів. Якщо ряд є збіжним, а ряд з абсолютних величин розбігається, то такий знакозмінний ряд називається умовно збіжним. Ряд, члени якого по черзі є додатними та від’ємними, називається рядом з чергуванням знаків (або рядом Лейбніца).Такий ряд доцільно записувати у вигляді
Теорема Лейбніца. Якщо виконуються такі умови: 1) 2) послідовність то ряд Зауваження. Теорема Лейбніца надає достатню умову збіжності рядів з чергуванням знаків, отже, у випадку не монотонно спадної, але нескінченно малої послідовності
Зразки розв’язування задач
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.140.180 (0.01 с.) |


 . Це неправильна дробово-раціональна функція (степінь числівника не менший за степінь знаменника), отже, доцільно скористатися необхідною умовою збіжності.
. Це неправильна дробово-раціональна функція (степінь числівника не менший за степінь знаменника), отже, доцільно скористатися необхідною умовою збіжності. . За необхідною умовою збіжності ряд розбігається.
. За необхідною умовою збіжності ряд розбігається. .
. більший за степінь знаменника
більший за степінь знаменника  , отже, доцільно скористатися необхідною умовою збіжності.
, отже, доцільно скористатися необхідною умовою збіжності. . Ряд розбігається.
. Ряд розбігається.
 не існує, отже, за необхідною умовою збіжності ряд розбігається.
не існує, отже, за необхідною умовою збіжності ряд розбігається.
 , знаменник –
, знаменник – 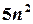 , отже,
, отже,  ~
~  .
. .
. .
.
 ~
~  ~
~  ;
; ~
~  ;
; ~
~  ~
~  .
. , який є збіжним, оскільки показник степеня
, який є збіжним, оскільки показник степеня  .
.
 .
.
 та оберемо ряд для порівняння.
та оберемо ряд для порівняння. ~
~  ~
~  .
. , який є розбіжним, оскільки показник степеня
, який є розбіжним, оскільки показник степеня  .
. .
. .
. ;
; .
. збігається, оскільки показник степеня
збігається, оскільки показник степеня  , отже, згідно з ознакою порівняння ряд
, отже, згідно з ознакою порівняння ряд  також буде збіжним.
також буде збіжним.
 ;
; .
. розбігається, оскільки показник степеня
розбігається, оскільки показник степеня  , отже, згідно з ознакою порівняння ряд
, отже, згідно з ознакою порівняння ряд  .
.
 ,
,  .
.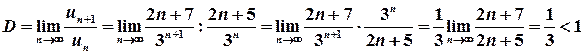 .
.
 , які складають арифметичну прогресію з першим членом 1 та різницею 2, тобто відповідають формулі
, які складають арифметичну прогресію з першим членом 1 та різницею 2, тобто відповідають формулі  . Знаменники дробів є факторіальними добутками, останні множники яких обчислюються як
. Знаменники дробів є факторіальними добутками, останні множники яких обчислюються як  . Тоді загальний член ряду має вигляд
. Тоді загальний член ряду має вигляд  . У цьому випадку також доцільно скористатися ознакою Даламбера.
. У цьому випадку також доцільно скористатися ознакою Даламбера.



 .
.
 ,
,  .
. використаємо наслідок першої важливої границі
використаємо наслідок першої важливої границі  , тобто
, тобто  при
при  .
.



 . Скористаємося ознакою порівняння.
. Скористаємося ознакою порівняння. .
. .
. буде розбіжним за необхідною умовою збіжності
буде розбіжним за необхідною умовою збіжності  , тоді, згідно з ознакою порівняння, досліджуваний ряд
, тоді, згідно з ознакою порівняння, досліджуваний ряд 
 .
. ,
,  ,
,  більший за одиницю.
більший за одиницю. . Гармонічний ряд
. Гармонічний ряд 

 .
.
 .
.
 використаємо другу важливу границю
використаємо другу важливу границю  .
. .
.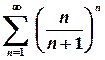
 . Скористаємося необхідною умовою збіжності.
. Скористаємося необхідною умовою збіжності. .
.
 . Ця функція неперервного аргументу для
. Ця функція неперервного аргументу для  набуває додатних значень та є спадною. Обчислимо невласний інтеграл першого роду від цієї функції та скористаємося інтегральною ознакою Коші.
набуває додатних значень та є спадною. Обчислимо невласний інтеграл першого роду від цієї функції та скористаємося інтегральною ознакою Коші.

 =
=
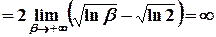 .
.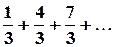 2.
2.  3.
3. 
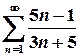 5.
5.  6.
6. 
 8.
8.  9.
9. 
 11.
11.  12.
12. 
 14.
14.  15.
15. 
 17.
17. 
 19.
19.  20.
20. 
 22.
22.  23.
23. 
 25.
25.  26.
26. 
 28.
28. 
 30.
30.  31.
31. 
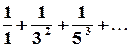 33.
33. 

 . 3. Збігається,
. 3. Збігається,  . 4. За необхідною умовою розбігається. 5. За необхідною умовою розбігається. 6. За необхідною умовою розбігається. 7. За необхідною умовою розбігається. 8. За необхідною умовою розбігається. 9. За необхідною умовою розбігається. 10. За граничною ознакою порівняння розбігається. 11. За граничною ознакою порівняння збігається. 12. За граничною ознакою порівняння розбігається. 13. За граничною ознакою порівняння збігається. 14. За ознакою порівняння розбігається. 15. За ознакою порівняння збігається. 16. За граничною ознакою порівняння розбігається. 17. За граничною ознакою порівняння збігається. 18. За інтегральною ознакою Коші ряд розбігається. 19. За інтегральною ознакою Коші ряд збігається. 20. За інтегральною ознакою Коші ряд збігається. 21. За ознакою Даламбера ряд розбігається. 22. За ознакою Даламбера ряд збігається. 23. За ознакою Даламбера ряд збігається. 24. За ознакою Даламбера ряд збігається. 25. За ознакою Даламбера ряд збігається. 26. За ознакою Даламбера ряд розбігається. 27. За ознакою Даламбера ряд збігається. 28. За радикальною ознакою Коші ряд збігається. 29. За радикальною ознакою Коші ряд збігається. 30. За радикальною ознакою Коші ряд розбігається. 31. За радикальною ознакою Коші ряд збігається. 32. За радикальною ознакою Коші ряд збігається. 33. За радикальною ознакою Коші ряд збігається. 34. За радикальною ознакою Коші ряд розбігається.
. 4. За необхідною умовою розбігається. 5. За необхідною умовою розбігається. 6. За необхідною умовою розбігається. 7. За необхідною умовою розбігається. 8. За необхідною умовою розбігається. 9. За необхідною умовою розбігається. 10. За граничною ознакою порівняння розбігається. 11. За граничною ознакою порівняння збігається. 12. За граничною ознакою порівняння розбігається. 13. За граничною ознакою порівняння збігається. 14. За ознакою порівняння розбігається. 15. За ознакою порівняння збігається. 16. За граничною ознакою порівняння розбігається. 17. За граничною ознакою порівняння збігається. 18. За інтегральною ознакою Коші ряд розбігається. 19. За інтегральною ознакою Коші ряд збігається. 20. За інтегральною ознакою Коші ряд збігається. 21. За ознакою Даламбера ряд розбігається. 22. За ознакою Даламбера ряд збігається. 23. За ознакою Даламбера ряд збігається. 24. За ознакою Даламбера ряд збігається. 25. За ознакою Даламбера ряд збігається. 26. За ознакою Даламбера ряд розбігається. 27. За ознакою Даламбера ряд збігається. 28. За радикальною ознакою Коші ряд збігається. 29. За радикальною ознакою Коші ряд збігається. 30. За радикальною ознакою Коші ряд розбігається. 31. За радикальною ознакою Коші ряд збігається. 32. За радикальною ознакою Коші ряд збігається. 33. За радикальною ознакою Коші ряд збігається. 34. За радикальною ознакою Коші ряд розбігається.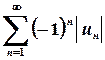 .
. ; та
; та ,
,  , …
, …  …є монотонно спадною,
…є монотонно спадною,


