
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достатні умови збіжності знакододатних рядівСодержание книги
Поиск на нашем сайте
Ознака порівняння. Якщо для членів знакододатних рядів справджується нерівність Якщо для членів знакододатних рядів справджується нерівність Якщо для членів знакододатних рядів має місце умова Найчастіше для порівняння використовується узагальнений гармонічний ряд (або ряд Діріхле) випадку
Ознака Даламбера. Ряд
Радикальна ознака Коші Ряд Інтегральна ознака Коші Нехай загальний член ряду задано рівністю
При розв’язуванні задач доцільно обирати ознаку для дослідження, користуючись порадами, які наведені у вигляді таблиці.
Зразки розв’язання задач
Скласти формулу загального члена
1. Члени ряду є дробами. Послідовність числівників Умову, яка задає
2. Члени ряду є дробами. Числівник дробу складається з двох множників, перший з яких є факторіалом члена арифметичної прогресії з першим членом 1 та різницею 2, отже, задається як
Тоді Зауваження. Для факторіального добутку доцільно при побудові формули для
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.72.27 (0.006 с.) |

 , та ряд
, та ряд  є збіжним, то ряд
є збіжним, то ряд  також збігається.
також збігається.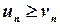 , та ряд
, та ряд 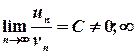 , то ряди
, то ряди 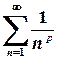 . Цей ряд збігається, якщо
. Цей ряд збігається, якщо  , та розбігається у
, та розбігається у .
. менший за 1, та розбігається, якщо це число більше за 1. У випадку
менший за 1, та розбігається, якщо це число більше за 1. У випадку  поведінку ряду за допомогою ознаки Даламбера визначити неможливо.
поведінку ряду за допомогою ознаки Даламбера визначити неможливо. менший за 1, та розбігається, якщо це число більше за 1. У випадку
менший за 1, та розбігається, якщо це число більше за 1. У випадку  поведінку ряду за допомогою радикальної ознаки Коші визначити неможливо.
поведінку ряду за допомогою радикальної ознаки Коші визначити неможливо. , та функція
, та функція  є додатною та спадною на проміжку
є додатною та спадною на проміжку  . Тоді невласний інтеграл
. Тоді невласний інтеграл  та ряд
та ряд  ,
,  ,
,  ,
,  , аргументами яких є правильний алгебраїчний дріб
, аргументами яких є правильний алгебраїчний дріб
 ,
, 
 ;
;  ;
; 
 Зауваження 1. Теоретично дослідження збіжності будь-якого числового ряду повинно починатися з перевірки необхідної умови збіжності. Але ця процедура досить часто є нетривіальною і, що дуже важливо, не завжди надає можливість зробити остаточний висновок. Отже, ми будемо вважати за доцільне застосовувати необхідну ознаку у тих випадках, коли є обгрунтовані припущення щодо її ефективності.
Зауваження 1. Теоретично дослідження збіжності будь-якого числового ряду повинно починатися з перевірки необхідної умови збіжності. Але ця процедура досить часто є нетривіальною і, що дуже важливо, не завжди надає можливість зробити остаточний висновок. Отже, ми будемо вважати за доцільне застосовувати необхідну ознаку у тих випадках, коли є обгрунтовані припущення щодо її ефективності. та знайти
та знайти  для заданого числового ряду:
для заданого числового ряду:
 складає арифметичну прогресію з першим членом 1 та різницею 3, отже, задається з урахуванням формули загального члену арифметичної прогресії
складає арифметичну прогресію з першим членом 1 та різницею 3, отже, задається з урахуванням формули загального члену арифметичної прогресії  як
як  =
=  . Послідовність знаменників
. Послідовність знаменників  складає геометричну прогресію з першим членом 3 та знаменником 5, отже, за формулою загального члену геометричної прогресії
складає геометричну прогресію з першим членом 3 та знаменником 5, отже, за формулою загального члену геометричної прогресії  задається як
задається як  . Таким чином, загальний член ряду задається рівністю
. Таким чином, загальний член ряду задається рівністю  .
. на
на  , отже,
, отже, .
.
 . Послідовність других множників
. Послідовність других множників  відповідає формулі
відповідає формулі  . Знаменник кожного з дробів є добутком попереднього знаменника та нового множника, який складає з існуючими арифметичну прогресію з першим членом 2 та різницею 3. Таким чином, послідовність нових множників відповідає формулі
. Знаменник кожного з дробів є добутком попереднього знаменника та нового множника, який складає з існуючими арифметичну прогресію з першим членом 2 та різницею 3. Таким чином, послідовність нових множників відповідає формулі  , а весь знаменник має вигляд
, а весь знаменник має вигляд  . Таку послідовність будемо надалі називати факторіальним добутком. Отже, формулою загального члена ряду є рівність
. Таку послідовність будемо надалі називати факторіальним добутком. Отже, формулою загального члена ряду є рівність .
. .
.


