
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудувати ряд Фур’є для заданої функціїСодержание книги
Поиск на нашем сайте
1.
тобто це функція загального виду, отже, ряд Фур’є цієї функції має вигляд
Обчислимо коефіцієнти цього ряду.
Таким чином, ряд Фур’є має вигляд
2.
тобто функція є парною, а її ряд Фур’є має вигляд
Обчислимо коефіцієнти ряду.
Отже, 3. Функція
Рис.4.1 Графік даної функції симетричний відносно початку координат, тому функція непарна, періодична с періодом 2π. Ряд Фур’є має вигляд
Задамо функцію
Тоді
Таким чином, ряд Фур’є функції, зображеної на рис.1, виглядає так:
Завдання для самостійної роботи
Знайти ряд Фур’є для функцій 1. 2. 3. На проміжку
Рис. 4.2 Відповіді 1. 2. 3.
4.3. Ряди Фур’є 2 l - періодичних функцій
Якщо f(x) є функцією періоду 2 l, її розвинення в ряд Фур’є має вигляд
де коефіцієнти обчислюються за формулами
Для парних функцій формули мають вигляд
а для непарних –
Зразки розв’язання задач
1. Функція є періодичною з періодом
отже, Обчислимо коефіцієнти ряду.
Остаточно
2. Функція є періодичною з періодом
Обчислимо коефіцієнти ряду.
Таким чином, ряд має вигляд
3. Функція має період
Обчислимо коефіцієнти ряду.
Отриманий результат справджується для Окремо обчислимо коефіцієнт
Таким чином, Отриманий результат є очікуваним, оскільки функція
4.На проміжку
Рис.4.3
Період функції 2 l= 8, отже, півперіод l= 4. Графік є симетричним відносно осі
Задамо функцію аналітично. Запишемо рівняння прямої, яка проходить через точки
Користуючись рівнянням
Таким чином, Якщо Остаточно
Обчислимо коефіцієнти Фур’є:
Зауваження. Також цілком коректною є задача побудови ряду Фур’є для функції, яку задано лише на скінченому проміжку
Завдання для самостійної роботи
Знайти ряд Фур’є для функцій. 1. 2.
Відповіді 1. 2.
4.4. Ряди Фур’є для функцій, заданих на проміжку
Якщо функцію У випадку, коли функцію продовжено на проміжку
де
Якщо продовження є непарним, отримують розвинення заданої функції за синусами:
де Аналогічно будується розвинення в ряд Фур’є функцій, заданих на проміжку
Зразки розв’язання задач
1. Побудувати розвинення в ряд Фур’є функції а) за синусами; б) за косинусами.
а) Функцію задано на проміжку
Обчислимо коефіцієнти цього ряду.
Остаточно
б) Розвинення функції в ряд Фур’є за косинусами має вид
Обчислимо коефіцієнти ряду.
Таким чином,
2. Побудувати ряди Фур’є за синусами та за косинусами функції, заданої графічно.
Рис.4.4
Задамо функцію аналітично. Очевидно, що, якщо
Функцію задано на проміжку а) Розвинення в ряд за синусами має вид
Обчислимо коефіцієнти цього ряду.
Тоді
б) Побудуємо ряд за косинусами:
Отже,
Завдання для самостійної роботи Побудувати розвинення в ряди Фур’є за синусами та за косинусами функцій: 1. 2. 3.
Рис.4.5
Відповіді
1. а) б) 2. а) б) 3. а) б)
ЛІТЕРАТУРА
1. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2006. – 648 с. 2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления.
В 3-х т. Т. 2: М: – ФИЗМАТЛИТ, 2001. – 810 с. 3. Пискунов Н.С. Дифференциальное и интегральное исчисления: Учеб. для втузов. В 2-х т.: Т. 2: – М: – Интеграл-Пресс, 2004. – 544 с. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. 2: – М.: Оникс, 2006. – 416 с. 5. Сборник задач по высшей математике. 2 курс / К.Н. Лунгу, В.П. Норин, Д.Т. Письменный и др. – М.: АЙРИС-пресс, 2009. – 592 с. З М І С Т Вступ ……………………………………………………………………………….3
Розділ 1 Числові ряди 1.1. Знакододатні ряди…………………………………………………………….4 1.2. Знакозмінні ряди…………………………………………………………….19
Розділ 2 Степеневі ряди 2.1. Збіжність степеневих рядів…….……………………………………………23 2.2. Розвинення функцій в степеневі ряди……………………………………...32
Розділ 3 Застосування рядів 3.1. Наближене обчислення значень функцій та визначених інтегралів…………………………………………………………………......50 3.2. Інтегрування диференціальних рівнянь за допомогою степеневих рядів……………………………………………………………..60
Розділ 4 Ряди Фур’є 4.1. Основні формули…………………………………………………………….66 4.2. Розвинення в ряди Фур’є 2π -періодичних функцій…………..…………...68 4.3. Ряди Фур’є 2l -періодичних функцій…………………………..…………..74 4.4. Ряди Фур’є для функцій, заданих на проміжку
ЛІТЕРАТУРА ……………………………………………………………………..86 Навчальне видання Кадильникова Тетяна Михайлівна Кагадій Лариса Петрівна Кочеткова Інна Борисівна Сушко Лариса Федорівна Запорожченко Олена Євгенівна
Вища математика в прикладах та задачах. Частина V Навчальний посібник
Тематичний план 2011, поз. Підписано до друку. Формат 60х84 1/16. Папір друк. Друк плоский. Облік.-вид. арк.. Умов. друк. арк.. Тираж 100 пр. Замовлення № Національна металургійна академія України 49600, м. Дніпропетровськ-5, пр. Гагаріна, 4 __________________________________ Редакційно-видавничий відділ НМетАУ
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 921; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.13.203 (0.011 с.) |

 ,
, 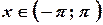 ;
;  .
. ,
, .
.


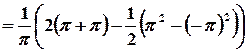
 ;
;





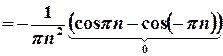
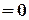 ;
;
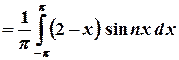
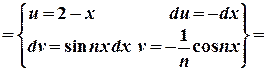


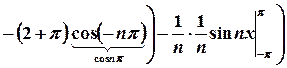


 .
. .
.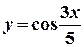 ,
,  ;
;  ,
, .
.

 ;
;







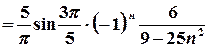
 .
. .
. задана графічно.
задана графічно.
 де
де  .
. та
та  .Запишемо рівняння прямої
.Запишемо рівняння прямої  :
:
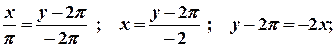
 .
.



 .
.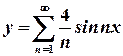 .
. .
. .
. функцію задано графічно;
функцію задано графічно;  .
.
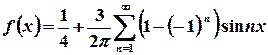 .
. .
.
 ,
, ,
, ,
, .
. ,
, 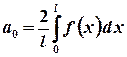 ,
,  ,
,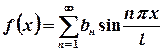 ,
,  .
. ,
,  ;
; 
 , отже,
, отже, 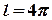 .
.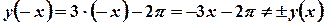 – функція загального вигляду,
– функція загального вигляду, .
.
 ;
;




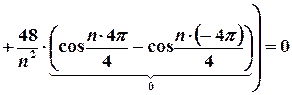 ;
;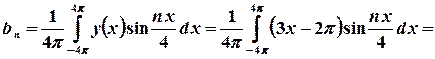
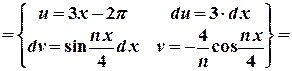






 .
.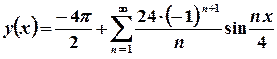 .
. ;
; 
 , отже,
, отже,  . Очевидно, що функція є ні парною, ні непарною, отже,
. Очевидно, що функція є ні парною, ні непарною, отже, .
. ,
,
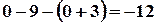 ,
,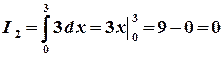 ,
, ;
;
 ,
,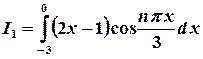





 ,
,
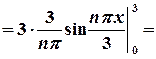
 ,
, ;
;
 ,
,
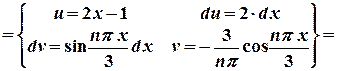



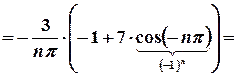
 ,
,



 ,
, .
. .
. ,
,  ;
;  .
. , отже,
, отже,  .
. – функція непарна, тобто її ряд Фур’є має вигляд
– функція непарна, тобто її ряд Фур’є має вигляд  .
.


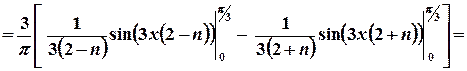
 .
. , оскільки застосування відомої формули з таблиці інтегралів можливо лише, якщо
, оскільки застосування відомої формули з таблиці інтегралів можливо лише, якщо  .
. :
:
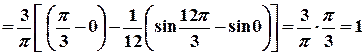 .
. , або
, або  періодичну з періодом
періодичну з періодом  функцію y=f(x) задано графічно.
функцію y=f(x) задано графічно.
 , тому функція парна та розкладається в ряд Фур’є за косинусами:
, тому функція парна та розкладається в ряд Фур’є за косинусами: .
. та
та  .
. , маємо
, маємо

 .
. для
для  .
.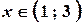 , то
, то  ; при
; при 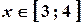
 .
. .
.

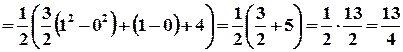 ;
;



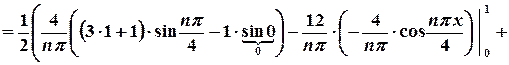


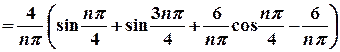 .
. .
.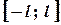 . Треба лише зауважити, що застосовувати отримане розвинення можна виключно для значень аргументу із зазначеного проміжку.
. Треба лише зауважити, що застосовувати отримане розвинення можна виключно для значень аргументу із зазначеного проміжку. .
.
 .
. .
.
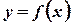 задано на проміжку
задано на проміжку  , то її визначення можна доповнити для проміжку
, то її визначення можна доповнити для проміжку  , та побудувати розвинення отриманої функції в ряд Фур’є.
, та побудувати розвинення отриманої функції в ряд Фур’є. ,
, .
. ,
, 
 , отже,
, отже,  . Розвинення в ряд Фур’є за синусами має вид
. Розвинення в ряд Фур’є за синусами має вид .
.







 .
. ,
, 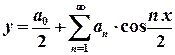 .
.
 ;
;



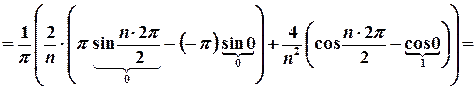

 .
. ,
, 
 , то
, то  , а для
, а для 
 , отже,
, отже, .
.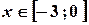 , тобто
, тобто  .
. .
.



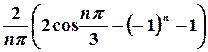 .
. ,
,  .
.

 .
.


 .
. ,
,  ,
,  .
. .
.

 ;
; .
. ;
; .
. ;
; .
.


