
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знайти область збіжності степеневого ряду.Содержание книги
Поиск на нашем сайте
9. Для заданого ряду
Інтервал збіжності ряду задається умовою
Узагальнений гармонічний ряд
Це ряд Лейбніца. Перевіримо, чи виконуються умови відповідної теореми. 1) 2)
За теоремою Лейбніца ряд є збіжним, тобто при Таким чином, областю збіжності досліджуваного ряду є
10. Якщо необхідно дослідити поведінку ряду за степенями
Це ряд з пропуском степенів, тому скористаємося ознакою Даламбера:
Нерівність
Дослідимо поведінку ряду на границях інтервалу збіжності.
Гармонічний ряд
Гармонічний ряд Таким чином, область збіжності ряду задається умовою
11. Введемо нову змінну Для цього ряду
Інтервалом збіжності допоміжного ряду буде
Це ряд Лейбніца. Перевіримо, чи виконуються умови відповідної теореми. 1) 2)
За теоремою Лейбніца ряд є збіжним, тобто при
Узагальнений гармонічний ряд Таким чином, область збіжності допоміжного ряду відповідає умові Тоді область збіжності основного ряду задається нерівністю
Отже, область збіжності заданого ряду – це проміжок
Завдання для самостійної роботи
1. З’ясувати, чи буде степеневий ряд
Знайти інтервал збіжності ряду: 2. 5
Знайти область збіжності ряду: 7. 10. 13. 16. 19
Відповіді. 1. Ряд збігається за ознакою Лейбніца. 2. 7. 11. 16.
Розвинення функцій у степеневі ряди
Якщо функція
Степеневий ряд у околі точки
Наведемо розвинення у ряд Маклорена деяких елементарних функцій та вкажемо інтервали збіжності цих рядів (у точках, що належать інтервалам збіжності, ряди збігаються до значень відповідних функцій у цих точках).
Степеневі ряди мають такі важливі властивості: а) степеневий ряд б) степеневий ряд
Зразки розв’язування задач
1.Знайти перші два ненульові члени розвинення у ряд Маклорена функції Ряд Маклорена має вигляд
Обчислимо значення заданої функції та декількох її перших похідних при
Тоді розвинення функції має вигляд
2. Розвинути у ряд Тейлора в околі точки Розвинення у ряд Тейлора полінома буде мати скінченну кількість ненульових членів.
Розвинути функцію у ряд Маклорена за допомогою табличних розвинень. Вказати інтервал збіжності отриманого ряду:
3. При побудові розвинення буде введено допоміжну змінну за аргументом складної функції.
Табличний ряд буде збігатися при
4.
Табличний ряд буде збігатися при
5.
Інтервал збіжності застосованого табличного ряду визначається нерівністю
Таким чином, інтервалом збіжності побудованого ряду буде
6.
Інтервал збіжності застосованого табличного ряду визначається нерівністю
Таким чином, інтервалом збіжності побудованого ряду буде
7. Задану функцію можна записати у вигляді Спочатку запишемо вказане табличне розвинення:
Повернемося до заданої функції:
Інтервал збіжності застосованого табличного ряду визначається нерівністю
Таким чином, інтервалом збіжності побудованого ряду буде
8. Задану функцію можна записати у вигляді Спочатку запишемо вказане табличне розвинення:
Повернемося до заданої функції:
Інтервал збіжності застосованого табличного ряду визначається нерівністю
Таким чином, інтервалом збіжності побудованого ряду буде
9.Розвинути в степеневий ряд функцію 1 спосіб. Ряд Тейлора для заданої функції має вигляд
Обчислимо у точці
Легко помітити, що значення похідних є додатними дробами, числівники яких мають факторіальний вигляд, а знаменники є степенями основи 3. Аналіз цих виразів приводить до висновку, що шукані значення похідних можна обчислити за формулою
Тоді ряд Тейлора для заданої функції має вигляд
Обчислимо радіус збіжності отриманого ряду.
Тоді ряд абсолютно збігається, якщо Таким чином, інтервал збіжності задається умовою
2 спосіб. Використаємо табличне розвинення у ряд Маклорена. Для цього виконаємо заміну змінної
Таким чином, шукане розвинення має вигляд
Інтервал збіжності застосованого табличного ряду визначається нерівністю
Таким чином, інтервалом збіжності побудованого ряду буде
10.Розвинути в степеневий ряд функцію 1 спосіб. Ряд Тейлора для заданої функції має вигляд
Обчислимо у точці
Легко помітити, що парні похідні дорівнюють 0, а значення непарних є знакозмінними дробами, числівники яких є степенями основи
Тоді ряд Тейлора для заданої функції має вигляд
Знайдемо інтервал збіжності ряду за допомогою ознаки Даламбера:
Нерівність
2 спосіб. Використаємо табличне розвинення у ряд Маклорена. Для цього виконаємо заміну змінної
Таким чином, шукане розвинення має вигляд
Табличний ряд буде збігатися при
11.Розвинути в степеневий ряд функцію 1 спосіб. Ряд Тейлора для заданої функції має вигляд
Обчислимо у точці
Аналіз цих виразів приводить до висновку, що шукані значення похідних можна обчислити за формулою
Тоді ряд Тейлора для заданої функції має вигляд
Обчислимо радіус збіжності отриманого ряду.
Таким чином, ряд буде збіжним при
2 спосіб. Використаємо табличне розвинення у ряд Маклорена. Для цього виконаємо заміну змінної
Таким чином, шукане розвинення має вигляд
Табличний ряд буде збігатися при
12.Розвинути в степеневий ряд функцію Побудуємо шукане розвинення за допомогою табличних розвинень у ряд Маклорена.Для цього виконаємо заміну змінної
Тоді
Умовами збіжності допоміжних рядів були нерівності
Остаточно
13.Розвинути в степеневий ряд функцію Побудуємо шукане розвинення за допомогою табличних розвинень у ряд Маклорена. Для цього виконаємо заміну змінної
Запишемо необхідне для подальшого розв’язування задачі табличне розвинення.
Отримуємо
Остаточно
14.Записати у вигляді ряду інтеграл зі змінною верхньою границею Запишемо розвинення у ряд Маклорена підінтегральної функції
Отриманий ряд збігається на всій множині дійсних чисел, отже, його можна почленно інтегрувати у будь-якому скінченному проміжку. Тоді з урахуванням того, що
Легко помітити, що отримане розвинення відповідає функції
15.Записати у вигляді ряду інтеграл зі змінною верхньою границею Запишемо розвинення у ряд Маклорена підінтегральної функції
Як відомо, інтервалом збіжності отриманого ряду є
Завдання для самостійної роботи
1. Знайти перші три ненульові члени розвинення у ряд Маклорена функції 2. Розвинути у ряд Тейлора в околі точки
Записати розвинення функції у ряд Маклорена. Вказати інтервал збіжності отриманого ряду. 3. 6. 9. Записати розвинення функції у ряд Тейлора в околі заданої точки. Вказати інтервал збіжності отриманого ряду. 10. 12. 14. 16. Записати у вигляді ряду інтеграл зі змінною верхньою границею. 17. Відповіді. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. Розділ 3. ЗАСТОСУВАННЯ РЯДІВ
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 796; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.209.231 (0.008 с.) |


 ,
,  .
.
 .
. . Дослідимо поведінку ряду на границях цього інтервалу.
. Дослідимо поведінку ряду на границях цього інтервалу. :
: 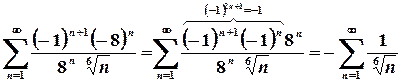 .
. є розбіжним
є розбіжним 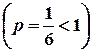 , отже, степеневий ряд при
, отже, степеневий ряд при  :
:  .
. ;
; ,
,  ,
,  , …
, … ,
,  .
. .
.
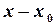 на границях інтервалу збіжності, доцільно ввести допоміжну змінну
на границях інтервалу збіжності, доцільно ввести допоміжну змінну  та розшукувати область збіжності отриманого ряду за новою змінною.
та розшукувати область збіжності отриманого ряду за новою змінною.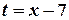 ;
;  .
. ,
, 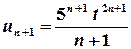 ;
;


 .
. справджується, якщо
справджується, якщо .
. ,
,  .
. є розбіжним, отже, степеневий ряд
є розбіжним, отже, степеневий ряд  ,
,  .
. , або
, або 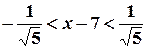 ,
,  .
.
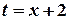 та знайдемо область збіжності отриманого ряду
та знайдемо область збіжності отриманого ряду  .
.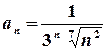 ,
, 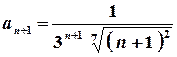 .
.
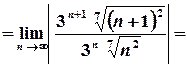
 .
. . Дослідимо поведінку ряду на границях інтервалу.
. Дослідимо поведінку ряду на границях інтервалу. ,
,  .
. ;
; ,
, 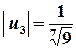 , …
, …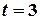 ,
, 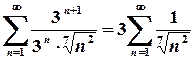 .
. є розбіжним
є розбіжним  , отже, степеневий ряд при
, отже, степеневий ряд при  .
. ;
;  .
. .
. збігатися у точці
збігатися у точці 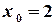 .
.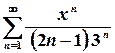 ; 3.
; 3.  ; 4.
; 4.  ;
; ; 6.
; 6. 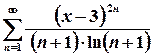 .
. ; 8.
; 8.  ; 9.
; 9. 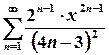 ;
; ; 11.
; 11.  ; 12.
; 12.  ;
;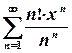 ; 14.
; 14. 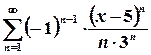 ; 15.
; 15.  ;
; ; 17.
; 17.  ; 18.
; 18.  ;
; ; 20.
; 20.  .
. ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5.  ; 6.
; 6.  ;
; ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10.  ; 12.
; 12.  ; 13.
; 13.  ; 14.
; 14.  ; 15.
; 15.  ;
; ; 17.
; 17. 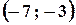 ; 18.
; 18.  ; 19.
; 19.  ; 20.
; 20.  .
. має в точці
має в точці  похідні будь-якого порядку, цій функції відповідає ряд Тейлора
похідні будь-якого порядку, цій функції відповідає ряд Тейлора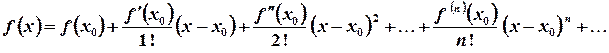 =
=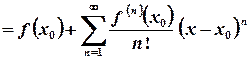 .
. має назву ряду Маклорена:
має назву ряду Маклорена: =
= .
. ;
;  .
.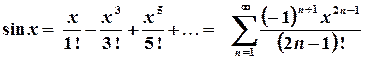 ;
;  ;
; 
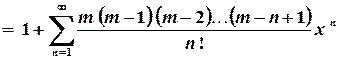 ;
;  .
. ;
; 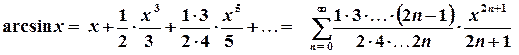 ;
;  ;
;  можна почленно інтегрувати, якщо проміжок інтегрування належить області збіжності ряду;
можна почленно інтегрувати, якщо проміжок інтегрування належить області збіжності ряду; .
. .
. .
. ;
; ,
,  ;
; ,
,  ;
;
 ,
, .
. ,
, .
. поліном
поліном  .
. .
.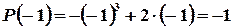 ;
; ,
,  ;
;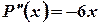 ,
,  ;
;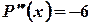 ,
,  ;
; .
. =
= .
.



 ;
;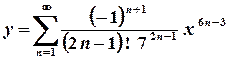 .
. , отже, побудований ряд буде збіжним при
, отже, побудований ряд буде збіжним при  .
.




 ;
; .
.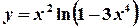




 ;
; .
. , отже, побудований ряд абсолютно збігається, якщо
, отже, побудований ряд абсолютно збігається, якщо .
. .
.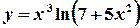




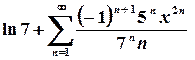 ;
; ;
; .
. .
. .
.
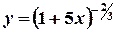 та скористатись табличним розвиненням у біноміальний ряд для
та скористатись табличним розвиненням у біноміальний ряд для  .
.



 .
.


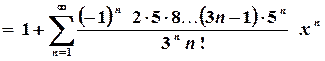 ;
; .
. .
. .
.
 та скористатись табличним розвиненням у біноміальний ряд для
та скористатись табличним розвиненням у біноміальний ряд для 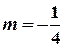 .
.

 .
.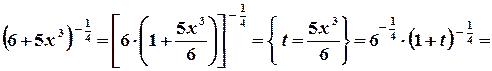


 ;
; ;
; .
. .
. .
.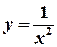 в околі точки
в околі точки  .
. .
. ;
;  ;
; ;
;  ;
; ;
; 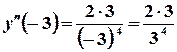 ;
; ;
;  .
. .
. ;
; .
. ,
,  ,
, .
. .
. .
. та перетворимо функцію до вигляду, який дозволяє використати вказане розвинення.
та перетворимо функцію до вигляду, який дозволяє використати вказане розвинення.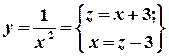

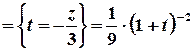 ;
;


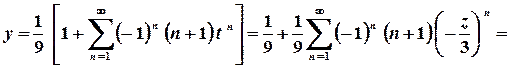

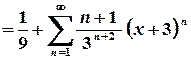 .
. .
. .
. .
.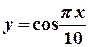 в околі точки
в околі точки 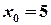 .
. .
. ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  .
. , а знаменники – степенями основи 10. Аналіз цих виразів приводить до висновку, що шукані значення похідних можна обчислити за формулою
, а знаменники – степенями основи 10. Аналіз цих виразів приводить до висновку, що шукані значення похідних можна обчислити за формулою .
. .
. ,
, ;
;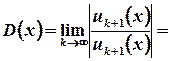

 .
. справджується для будь-якого значення
справджується для будь-якого значення  , отже, ряд буде збіжним для
, отже, ряд буде збіжним для  .
.
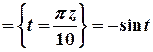


 .
. .
.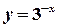 в околі точки
в околі точки  .
. .
.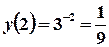 ;
; ,
,  ;
; ,
,  ;
; ,
,  .
. .
. .
. ,
, 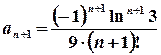 ,
,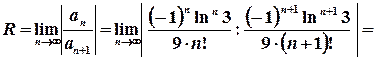
 .
.


 .
. .
. в околі точки
в околі точки  .
.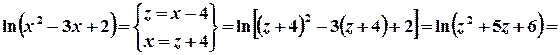
 .
.
 ;
;  ;
;  .
.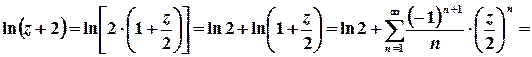
 ;
;  ;
; 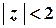 .
.


 .
. .
. ,
,  .
. в околі точки
в околі точки  .
.

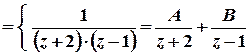 ;
;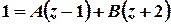 ;
;

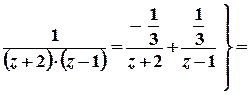
 .
.
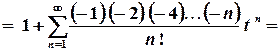
 .
.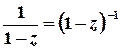
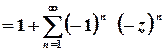
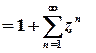 ;
;  .
.

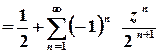 ;
;
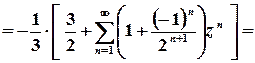

 ;
; .
. ,
,  .
. .
. .
.


 ,
,
 ;
;  .
. , маємо
, маємо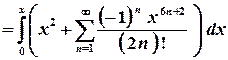

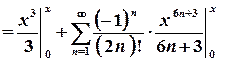
 .
. , яка є первісною для підінтегральної функції.
, яка є первісною для підінтегральної функції. .
. .
.
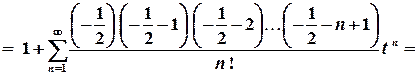


 .
. , крім того, можна показати за допомогою теореми Лейбніца, що цей ряд збігається також, якщо
, крім того, можна показати за допомогою теореми Лейбніца, що цей ряд збігається також, якщо  , отже, цей ряд можна почленно інтегрувати, якщо проміжок інтегрування повністю належить множині
, отже, цей ряд можна почленно інтегрувати, якщо проміжок інтегрування повністю належить множині  .
. =
=

 .
. .
. .
. . 4.
. 4.  . 5.
. 5.  .
. . 7.
. 7.  . 8.
. 8.  .
. .
.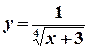 ,
,  . 11.
. 11.  ,
, 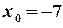 .
. ,
, 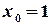 . 13.
. 13.  ,
,  .
. ,
,  . 15.
. 15. 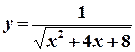 ,
, 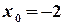 .
. ,
,  . 18.
. 18. 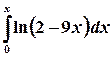 . 19.
. 19.  .
.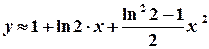 .
. .
. .
. .
. .
.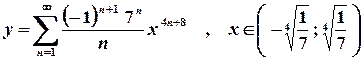 .
. .
.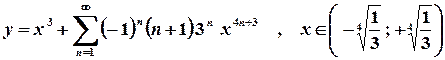 .
. .
. .
. .
. .
. .
. .
. .
.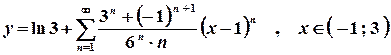 .
. .
. .
. .
.


