
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З’ясувати, чи буде заданий ряд розбіжним, абсолютно або умовно збіжним.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Члени заданого ряду мають різні знаки. Дослідимо цей ряд на абсолютну збіжність.
Узагальнений гармонічний ряд
2. Знаки членів ряду чергуються та відповідають залежності Перевіримо, чи виконуються умови теореми Лейбніца.
За необхідною умовою збіжності ряд розбігається.
3. Загальний член ряду задається формулою Перевіримо, чи виконуються умови теореми Лейбніца. 1) 2)
За теоремою Лейбніца ряд збігається. Дослідимо ряд з модулів
Узагальнений гармонічний ряд
Згідно з граничною ознакою порівняння знакододатний ряд
Зауваження. Умова спадності може виконуватися не з першого члена ряду. 4. Загальний член ряду задається формулою Перевіримо, чи виконуються умови теореми Лейбніца. 1) 2)
За теоремою Лейбніца ряд збігається. Дослідимо ряд з модулів
За ознакою Даламбера ряд Зауваження. У останньому прикладі можна обмежитися дослідженням ряду з модулів, оскільки при абсолютній збіжності автоматично забезпечується збіжність за Лейбніцем.
5. Дослідимо ряд з модулів
За ознакою Даламбера ряд Зауваження. Якщо при дослідженні ряду з модулів за радикальною ознакою Коші або за ознакою Даламбера з’ясовано, що цей ряд розбігається, то можна зробити висновок, що буде розбіжним і знакозмінний ряд, оскільки в таких випадках (
Завдання для самостійної роботи
1. 4. Відповіді. 1. Абсолютно збігається. 2. Розбігається. 3. Абсолютно збігається. 4. Умовно збігається. 5. Умовно збігається. 6. Абсолютно збігається.
Розділ 2 СТЕПЕНЕВІ РЯДИ Збіжність степеневих рядів
Розглянемо послідовність функцій
називається функціональним рядом. Ряд Множина всіх значень аргументу Сума Область збіжності функціонального ряду можна знайти за ознакою Даламбера або радикальною ознакою Коші.
Ознака Даламбера. Функціональний ряд
Якщо
Ознака Коші. Функціональний ряд
Якщо
Функціональний ряд вигляду Якщо Для будь-якого степеневого ряду Степеневий ряд Поведінка степеневого ряду на границях інтервалу збіжності потребує окремого дослідження. Якщо серед коефіцієнтів ряду немає таких, що дорівнюють нулю, (тобто у ряді немає пропуску степенів), радіус збіжності обчислюється за формулами
Якщо радіус збіжності Якщо ряд побудовано з пропуском степенів, для визначення інтервалу збіжності використовують умови для функціонального ряду, тобто нерівності
Зразки розв’язування задач
1. З’ясувати, чи буде степеневий ряд
Це знакододатний числовий ряд, який буде збіжним (
Знайти інтервал збіжності ряду: 2. Для даного ряду
Інтервал збіжності ряду
3. Для даного ряду
Інтервал збіжності ряду
4. Для даного ряду
Таким чином, ряд буде збіжним, якщо
5. Для даного ряду
Таким чином, ряд буде збіжним, якщо
6. Це ряд з пропуском степенів, тому скористаємося ознакою Даламбера:
Нерівність
Таким чином, інтервалом збіжності ряду буде
7. Це ряд з пропуском степенів, тому скористаємося ознакою Коші:
Нерівність
8. Це ряд з пропуском степенів, тому скористаємося ознакою Даламбера:
Нерівність
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.163.169 (0.011 с.) |



 збігається (оскільки показник степеня
збігається (оскільки показник степеня  ). Згідно з ознакою порівняння знакододатний ряд
). Згідно з ознакою порівняння знакододатний ряд 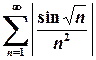 також збігається, отже знакозмінний ряд
також збігається, отже знакозмінний ряд 
 . Загальний член ряду задається формулою
. Загальний член ряду задається формулою  .
.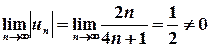 .
.
 .
. ;
; ,
,  ,
,  , …
, … ,
,  .
. .
. ~
~  .
. розбігається (оскільки показник степеня
розбігається (оскільки показник степеня  ).
). .
. збігається умовно.
збігається умовно.
 .
. ;
; ,
,  ,
,  ,
,  …
… ,
,  ,
,  , оскільки функція
, оскільки функція є монотонно спадною для
є монотонно спадною для  (
( ).
). . Скористаємося для цього ознакою Даламбера.
. Скористаємося для цього ознакою Даламбера. ,
,  .
. .
. збігається абсолютно.
збігається абсолютно.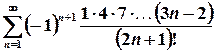
 . Скористаємося для цього ознакою Даламбера.
. Скористаємося для цього ознакою Даламбера. ,
,  .
.
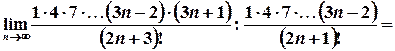

 .
. або
або  ) не виконується необхідна умова збіжності.
) не виконується необхідна умова збіжності. 2.
2.  3.
3. 
 5.
5.  6.
6. 
 . Вираз вигляду
. Вираз вигляду
 є збіжним в точці
є збіжним в точці 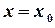 , якщо збігається числовий ряд
, якщо збігається числовий ряд  , та абсолютно збіжним, якщо збігається ряд
, та абсолютно збіжним, якщо збігається ряд  .
. , для яких функції
, для яких функції  ,
,  ,... визначені, а ряд
,... визначені, а ряд  називається п -ю частинною сумою ряду
називається п -ю частинною сумою ряду  – сумою цього ряду. Різницю
– сумою цього ряду. Різницю  називають залишком ряду.
називають залишком ряду.
 .
. , ряд є розбіжним, а поведінка функціонального ряду при тих значеннях аргументу, для яких
, ряд є розбіжним, а поведінка функціонального ряду при тих значеннях аргументу, для яких  , потребує окремого дослідження.
, потребує окремого дослідження. .
. , ряд є розбіжним, а поведінка функціонального ряду при тих значеннях аргументу, для яких
, ряд є розбіжним, а поведінка функціонального ряду при тих значеннях аргументу, для яких  , потребує окремого дослідження.
, потребує окремого дослідження. ,
,  називається степеневим, а числа
називається степеневим, а числа 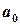 ,
,  ,
,  ,...
,... 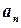 ,... – коєфіцієнтами цього ряду.
,... – коєфіцієнтами цього ряду. , степеневий ряд має вигляд
, степеневий ряд має вигляд  .
. існує таке число
існує таке число 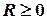 , що для
, що для  розглядуваний ряд збігається, а для
розглядуваний ряд збігається, а для  ряд є розбіжним. Інтервал
ряд є розбіжним. Інтервал  називається інтервалом збіжності, а число
називається інтервалом збіжності, а число  – радіусом збіжності цього ряду.
– радіусом збіжності цього ряду.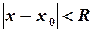 , тобто інтервалом збіжності такого ряду буде
, тобто інтервалом збіжності такого ряду буде  .
. або
або  .
. , ряд буде збіжним тільки в одній точці
, ряд буде збіжним тільки в одній точці  (або
(або 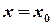 ).
).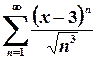 збігатися у точці
збігатися у точці  .
. .
. ).
).
 ;
;  .
. .
. .
.
 ,
,  ,
,  .
. .
. , або
, або 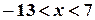 .
.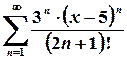
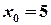 ,
,  ,
,  .
.
 .
. .
.
 ,
,  ,
,  .
.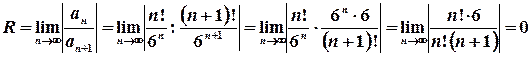
 .
.
 ,
, 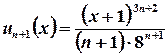 ;
;
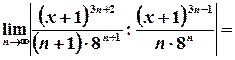
 .
. справджується, якщо
справджується, якщо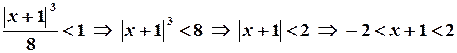 .
. .
.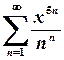
 ;
;
 .
. справджується для будь-якого значення
справджується для будь-якого значення 
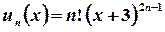 ,
, 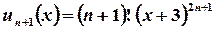 ;
; .
. , отже, ряд буде збіжним тільки для
, отже, ряд буде збіжним тільки для  .
.


