
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 8. Диференціальні рівнянняСтр 1 из 5Следующая ⇒
Розділ 8. Диференціальні рівняння Економічні задачі, що приводять до диференціальних рівнянь. Основні означення Розглянемо декілька прикладів. Нехай швидкість знецінювання устаткування внаслідок його зносу пропорційна в кожен даний момент часу його фактичній вартості. Початкова вартість – Введемо позначення. Нехай
з початковою умовою
Розв’язавши таке рівняння, одержимо відповідь на питання даної задачі. Розглянемо інший приклад. Нехай Відповідно до умови задачу можна сформулювати наступним чином. Запишемо інвестиції в вигляді: або Нехай торговими установами реалізується продукція, про яку в момент часу Відповідно до умови, рівняння для визначення Будемо вивчати звичайні диференціальні рівняння, тобто такі, у яких шукана функція є функцією однієї змінної.
Означення 8.1. Звичайним диференціальним рівнянням
При цьому функція Порядком диференціального рівняння будемо називати порядок найвищої похідної, що входить у нього. Так, наприклад, рівняння Означення 8.2. Розв'язком диференціального рівняння називається усяка функція Наприклад, функція Розв'язок диференціального рівняння називають інтегралом цього рівняння.
Диференціальні рівняння першого порядку З подільними змінними.
Розглянемо рівняння вигляду
яке називається рівнянням з розділеними змінними. Дане рівняння є рівністю двох диференціалів деяких функцій, з чого випливає, що функції або рівні, або розрізняються на довільну сталу. Розв'язок рівняння одержимо, проінтегрувавши рівність
Рівняння з подільними змінними має вигляд
Розділимо змінні, тобто перетворимо рівняння так, щоб біля диференціала
Проінтегрувавши, прийдемо до розв'язку у вигляді
Рівняння
Рівнянням такого типу є рівняння
Запишемо довільну сталу у вигляді
Звідки Розв’яжемо диференціальне рівняння
де шукана функція Розділимо змінні, одержимо
Обчислимо значення довільної сталої, виходячи з початкових умов. Отже формула для визначення чисельності населення має такий вигляд:
де Наприклад, якщо в деякий державі чисельність населення на даний момент часу 100 млн осіб, коефіцієнт природного приросту Приклад 8.1. Знайти частинний розв'язок диференціального рівняння Розв’язання. Дане рівняння є рівнянням з подільними змінними. Поділимо ліву і праву частину рівності на
Рівняння Бернуллі.
Рівняння Бернуллі має вигляд
Як бачимо, рівняння відрізняється від лінійного тільки множником
і замінимо Оскільки
тобто одержали лінійне рівняння відносно функції На практиці рівняння Бернуллі може розв’язуватися тим же способом, що і лінійне, без попереднього зведення його до лінійного рівняння. Приклад 8.5. Знайти загальний розв'язок рівняння
Розв’язання. Очевидно, що дане рівняння є рівнянням Бернуллі Підберемо
Складемо систему рівнянь: Розв’язуючи перше рівняння системи, знайдемо
Зі сталими коефіцієнтами.
Система двох лінійних однорідних диференціальних рівнянь зі сталими коефіцієнтами має вигляд
Розв'язки цієї системи мають такі властивості. 1. Якщо 2. Якщо З властивостей 1 і 2 випливає, що для будь-яких чисел Будемо шукати ненульові розв'язки системи (8.42) у вигляді
де Підставляючи функції (8.43) та їх похідні в рівняння системи (8.42) після скорочення на
Для того, щоб ця система рівнянь мала ненульовий розв'язок, необхідно і достатньо, щоб визначник системи дорівнював нулю. Таким чином число k повинно задовольняти рівняння
Рівняння (8.45) називається характеристичним рівнянням системи (8.42). Це рівняння другого степеня відносно
Позначимо ці розв'язки відповідно Лінійна комбінація цих розв'язків з довільними коефіцієнтами
також буде розв'язком системи (8.42). Якщо корені характеристичного рівняння (8.45) різні, то можна показати, що цей розв'язок буде загальним розв'язком системи (8.42). У випадку, якщо корені характеристичного рівняння комплексно-спряжені: У випадку кратних коренів характеристичного рівняння відшукання загального розв'язку системи (8.42) значно складніше. Приклад 8.17. Розв’язати систему рівнянь
Розв’язання. Характеристичне рівняння матриці системи має вигляд Після перетворень одержуємо два різних дійсних корені рівняння
При
Очевидно, що система має незліченну множину розв'язків, яку можна виразити залежністю
Аналогічно попередня система має незліченну множину розв'язків, яку можна виразити залежністю Отже, загальний розв'язок заданої системи рівнянь:
Задачі економічної динаміки Диференціальні рівняння знаходять достатньо широке застосування в моделях економічної динаміки, в яких відображується не тільки залежність змінних від часу, але й їх взаємозв’язок у часі. Розглянемо деякі (прості) задачі макроекономічної динаміки. Нехай Позначимо через
Тут знехтуємо часом між закінченням виробництва продукції та її реалізацією, тобто вважаємо, що інвестиційний лаг дорівнює нулю. Вважаючи, що розмір інвестицій
де коефіцієнт пропорційності Підставляючи останній вираз (8.48) для
де Отримано диференціальне рівняння – з подільними змінними. Розв’язуючи його, приходимо до функції Зазначимо, що рівняння (8.49) описує також зростання народонаселення (демографічний процес), динаміку росту цін при сталій інфляції, процес радіоактивного розпаду та ін. На практиці умова насиченості ринку може бути прийнятною тільки для достатньо вузького часового інтервалу. В загальному випадку крива попиту, тобто залежність ціни
залишаючись як і раніше рівнянням з подільними змінними. Оскільки всі співмножники у правій частині рівняння додатні, то
Нагадаємо, що еластичність попиту (відносно ціни) визначається формулою
і умова Таким чином, якщо попит еластичний, тобто Приклад 8.18. Знайти вираз для обсягу реалізованої продукції Розв’язання. Рівняння (8.50) в цьому випадку приймає такий вигляд: Враховуючи, що Графік даної функції схематично зображений на рис. 8.2. У даному випадку еластичність попиту задається функцією
Рис. 8.2. Крива, зображена на рис. 8.4, називається логістичною. Подібні криві описують процес розповсюдження інформації (реклами), динаміку епідемій, процес розмноження бактерій в обмеженому середовищі та ін. Розглянемо тепер іншу задачу. Прибуток
Як і раніше в моделі природного росту, будемо вважати, що швидкість збільшення прибутку пропорційна розміру інвестицій, тобто справедлива рівність
де Розглянемо поведінку функції прибутку Нехай
що рівносильне рівнянню (8.49) при В ряді випадків тип функції споживання Приклад 8.19. Знайти функцію прибутку
Розв’язання. Із співвідношень (8.51) і (8.52) маємо рівняння
тобто функція прибутку задовольняє лінійне неоднорідне рівняння першого порядку. Будемо шукати розв’язок у вигляді Тоді маємо Розглянемо економічну модель Е.Д. Домара. Основні припущення цієї моделі такі: 1. Будь-яка зміна швидкості грошового потоку 2. Швидкість зміни попиту
3. Економічний потенціал
В моделі Домара передбачається, що весь економічний потенціал повністю використовується, тобто
Підставляючи (8.54) та (8.55) в (8.56), маємо
Щоб знайти функцію
Потенціюючи останню рівність, одержуємо остаточний вираз для
де Таким чином, для того, щоб підтримувати рівновагу між обсягом вироблених благ та сукупним попитом на них, швидкість грошового потоку повинна зростати з експоненціальною швидкістю, згідно з формулою (8.58). Модель Домара – це типовий приклад моделі зростання, що записується у вигляді одного або декількох диференціальних рівнянь.
Вправи 8.1. Показати, що функція 8.2–8.24. Знайти загальний розв'язок диференціальних рівнянь першого порядку. 8.2. 8.4. 8.6. 8.8. 8.9. 8.11. 8.13. 8.15. 8.17. 8.19. 8.21. 8.23. 8.25–8.27. Знайти частинні розв'язки диференціальних рівнянь першого порядку, що задовольняють заданим початковим умовам. 8.25. 8.26. 8.27. 8.28–8.32. Знайти загальні розв'язки диференціальних рівнянь другого порядку, що допускають зниження порядку. 8.28. 8.29. 8.30. 8.31. 8.32. 8.33–8.34. Знайти частинні розв'язки диференціальних рівнянь другого порядку, які допускають зниження порядку та задовольняють заданим початковим умовам. 8.33. 8.34. 8.35–8.44. Знайти загальні розв'язки лінійних однорідних диференціальних рівнянь другого порядку. 8.35. 8.37. 8.39. 8.41.. 8.43. 8.45–8.53. Знайти загальні розв'язки лінійних неоднорідних диференціальних рівнянь. 8.45. 8.47. 8.49. 8.51. 8.53. 8.54–8.61. Знайти загальні розв'язки лінійних неоднорідних диференціальних рівнянь методом варіації довільних сталих. 8.54. 8.56. 8.58. 8.60. 8.62–8.64. Знайти частинні розв'язки лінійних диференціальних рівнянь другого порядку, що задовольняють заданим початковим умовам. 8.62. 8.63. 8.64. 8.65–8.72. Розв’язати системи диференціальних рівнянь.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.160.156 (0.228 с.) |
 . Поставимо питання: якою буде вартість устаткування після
. Поставимо питання: якою буде вартість устаткування після 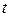 років?
років?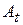 – вартість устаткування в момент
– вартість устаткування в момент 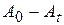 . Швидкість знецінювання тоді буде похідною за часом, тобто
. Швидкість знецінювання тоді буде похідною за часом, тобто 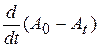 , і вона пропорційна фактичній вартості в даний момент
, і вона пропорційна фактичній вартості в даний момент 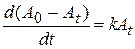
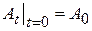 .
. – кількість продукції, що випускається галуззю за час
– кількість продукції, що випускається галуззю за час 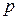 – ціна продукції. Сума інвестицій (засобів, спрямованих на розширення виробництва)
– ціна продукції. Сума інвестицій (засобів, спрямованих на розширення виробництва) 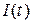 пропорційна доходові
пропорційна доходові  з коефіцієнтом пропорційності
з коефіцієнтом пропорційності  (
( ,
, 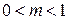 ). Збільшення швидкості випуску продукції пропорційно збільшенню інвестицій з коефіцієнтом пропорційності
). Збільшення швидкості випуску продукції пропорційно збільшенню інвестицій з коефіцієнтом пропорційності  . Потрібно знайти кількість продукції, що випускається галуззю за час
. Потрібно знайти кількість продукції, що випускається галуззю за час 
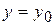 .
. . Тоді
. Тоді 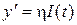 ,
,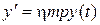 . Позначимо
. Позначимо 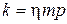 . Тоді рівняння набуде вигляду
. Тоді рівняння набуде вигляду  , розв’язавши його одержимо відповідь на питання задачі.
, розв’язавши його одержимо відповідь на питання задачі. знає лише
знає лише 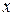 покупців. Після проведення рекламних оголошень швидкість зміни числа знаючих про продукцію покупців пропорційна як числу знаючих про товар покупців, так і числу покупців, що про нього ще не знають. Відомо, що в початковий момент часу
покупців. Після проведення рекламних оголошень швидкість зміни числа знаючих про продукцію покупців пропорційна як числу знаючих про товар покупців, так і числу покупців, що про нього ще не знають. Відомо, що в початковий момент часу  про товар довідалося
про товар довідалося 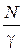 осіб (час відраховується після рекламних оголошень);
осіб (час відраховується після рекламних оголошень); 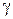 – задане число. Знайти закон зміни в залежності від часу числа
– задане число. Знайти закон зміни в залежності від часу числа 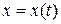 має вигляд
має вигляд 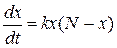 , де
, де 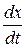 – швидкість зміни числа знаючих про товар покупців;
– швидкість зміни числа знаючих про товар покупців; 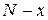 ) – число не знаючих про товар у момент часу
) – число не знаючих про товар у момент часу  – додатній коефіцієнт пропорційності. Початкова умова:
– додатній коефіцієнт пропорційності. Початкова умова: 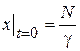 .
.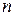 -го порядку називається рівняння, що пов'язує незалежну змінну
-го порядку називається рівняння, що пов'язує незалежну змінну 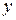 і її похідні
і її похідні  ,
,  ,...,
,..., 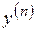 :
: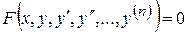 . (8.1)
. (8.1)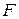 може явно не містити у собі
може явно не містити у собі 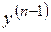 , але обов'язково повинна містити –
, але обов'язково повинна містити – 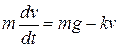 ,
,  ,
, 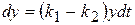 є диференціальними рівняннями першого порядку, а рівняння
є диференціальними рівняннями першого порядку, а рівняння  є диференціальним рівнянням другого порядку.
є диференціальним рівнянням другого порядку.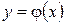 , що задовольняє його.
, що задовольняє його. є розв'язком рівняння
є розв'язком рівняння 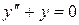 , тому що
, тому що 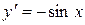 ,
,  і, підставляючи
і, підставляючи 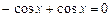 , що вірно для будь-якого
, що вірно для будь-якого  , (8.5)
, (8.5) .
.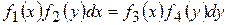 . (8.6)
. (8.6)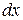 стояла множником функція аргументу
стояла множником функція аргументу 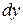 відповідно функція аргументу
відповідно функція аргументу  , одержимо рівняння з розділеними змінними
, одержимо рівняння з розділеними змінними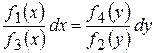 .
.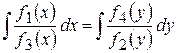 .
. є рівнянням з подільними змінними, тільки якщо
є рівнянням з подільними змінними, тільки якщо  , тоді замінивши
, тоді замінивши  і, помноживши рівняння на
і, помноживши рівняння на 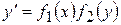 ,
, 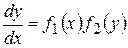 ,
,  ,
, 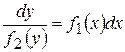 ,
, 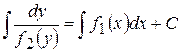 .
.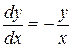 ,
,  ,
,  .
. , що не змінить її змісту, тоді
, що не змінить її змісту, тоді .
.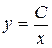 – загальний розв'язок рівняння.
– загальний розв'язок рівняння.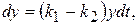
 .
. . Проінтегрувавши, знайдемо, що
. Проінтегрувавши, знайдемо, що  ,
, 
 і, остаточно,
і, остаточно, 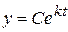 – загальний розв'язок диференціального рівняння.
– загальний розв'язок диференціального рівняння.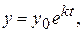
 – численність населення в початковий момент часу;
– численність населення в початковий момент часу;  , то через 5 років чисельність населення цієї держави буде дорівнювати:
, то через 5 років чисельність населення цієї держави буде дорівнювати: 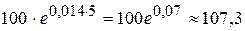 млн осіб.
млн осіб.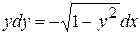 , що задовольняє початковій умові
, що задовольняє початковій умові  .
.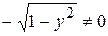 , одержимо:
, одержимо: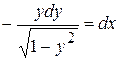 ,
, 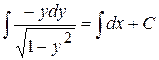 ,
, 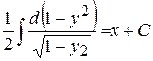 , або
, або 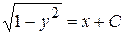 . Звідки
. Звідки  – інтеграл диференціального рівняння. Графіком інтеграла даного диференціального рівняння є сім’я кіл з центром у точці
– інтеграл диференціального рівняння. Графіком інтеграла даного диференціального рівняння є сім’я кіл з центром у точці  на вісі абсцис і радіусом
на вісі абсцис і радіусом 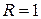 . Надаючи
. Надаючи  різні значення, одержимо різні інтегральні криві сім’ї. Щоб знайти частинний розв'язок рівняння, підставимо значення у загальний розв'язок і обчислимо відповідне значення
різні значення, одержимо різні інтегральні криві сім’ї. Щоб знайти частинний розв'язок рівняння, підставимо значення у загальний розв'язок і обчислимо відповідне значення 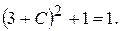 Звідки
Звідки 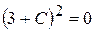 , або
, або 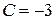 . Отже, частинним розв'язком рівняння є функція
. Отже, частинним розв'язком рівняння є функція  .
.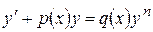 . (8.11)
. (8.11)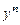 у правій частині рівняння. Покажемо, що це рівняння приводиться до лінійного. Поділимо рівняння на
у правій частині рівняння. Покажемо, що це рівняння приводиться до лінійного. Поділимо рівняння на 
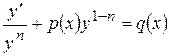
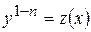 , тоді
, тоді 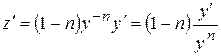 .
. , то рівняння набуває вигляду
, то рівняння набуває вигляду ,
,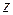 .
.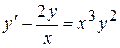 .
.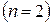 . Знайдемо розв'язок у вигляді
. Знайдемо розв'язок у вигляді 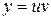 .
.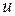 і
і  так, щоб їх добуток задовольняв рівняння. Підставимо в рівняння
так, щоб їх добуток задовольняв рівняння. Підставимо в рівняння 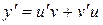 , одержимо
, одержимо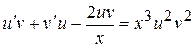 ,
, 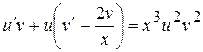 .
.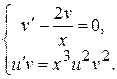
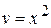 . Підставляючи знайдену функцію в друге рівняння системи, одержуємо
. Підставляючи знайдену функцію в друге рівняння системи, одержуємо 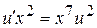 чи
чи 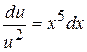 . Звідки
. Звідки  ,
,  . Загальний розв'язок рівняння:
. Загальний розв'язок рівняння: 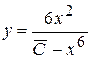 .
.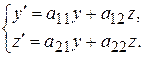 (8.42)
(8.42) ,
, 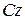 – де
– де  ,
, 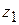 і
і 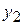 ,
, 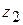 – розв'язки системи (8.42), то функції
– розв'язки системи (8.42), то функції  ,
, 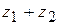 також будуть розв'язками системи.
також будуть розв'язками системи. ,
,  лінійна комбінація розв'язків
лінійна комбінація розв'язків 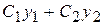 ,
, 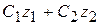 також є розв'язком системи.
також є розв'язком системи.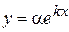 ,
, 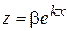 , (8.43)
, (8.43)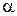 ,
, 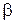 ,
,  і перенесення всіх членів в одну частину рівності, одержуємо
і перенесення всіх членів в одну частину рівності, одержуємо (8.44)
(8.44)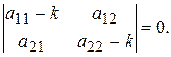 (8.45)
(8.45) і
і 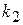 . Кожному з цих коренів відповідає ненульовий розв'язок системи (8.44).
. Кожному з цих коренів відповідає ненульовий розв'язок системи (8.44). ,
,  ,
, 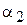 ,
,  . Тоді ненульові розв'язки даної системи диференціальних рівнянь (8.42) матимуть вигляд:
. Тоді ненульові розв'язки даної системи диференціальних рівнянь (8.42) матимуть вигляд: 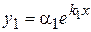 ,
, 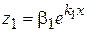 ,
, 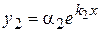 ,
,  .
.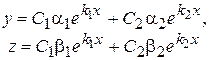 (8.46)
(8.46)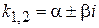 , то знайдені зазначеним вище методом комплексні розв'язки можна замінити дійсними розв'язками, відокремлюючи дійсні і уявні частини їх складовими функціями.
, то знайдені зазначеним вище методом комплексні розв'язки можна замінити дійсними розв'язками, відокремлюючи дійсні і уявні частини їх складовими функціями.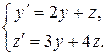
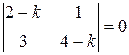 . Звідки
. Звідки 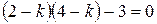 .
. ,
, 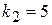 . Отже, загальний розв'язок заданої системи рівнянь має вигляд (8.46):
. Отже, загальний розв'язок заданої системи рівнянь має вигляд (8.46):
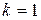 система (8.44) для визначення чисел
система (8.44) для визначення чисел 
 . Приймаючи для конкретності
. Приймаючи для конкретності 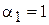 , одержуємо
, одержуємо  . При
. При 
 , Приймаючи
, Приймаючи 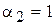 , одержимо
, одержимо 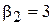 .
.
 – обсяг продукції деякої галуззі, яка реалізована на момент часу
– обсяг продукції деякої галуззі, яка реалізована на момент часу 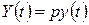 .
.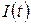 розмір інвестицій, що направляються на розширення виробництва. В моделі природного росту вважають, що швидкість випуску продукції (акселерація) пропорційна величині інвестицій, тобто
розмір інвестицій, що направляються на розширення виробництва. В моделі природного росту вважають, що швидкість випуску продукції (акселерація) пропорційна величині інвестицій, тобто . (8.47)
. (8.47) , (8.48)
, (8.48)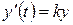 , (8.49)
, (8.49)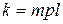 .
.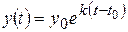 , де
, де 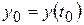 .
.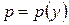 (зі збільшенням обсягу виробленої продукції її ціна падає внаслідок насиченості ринку). Тому модель зростання за умов конкурентного ринку приймає такий вигляд:
(зі збільшенням обсягу виробленої продукції її ціна падає внаслідок насиченості ринку). Тому модель зростання за умов конкурентного ринку приймає такий вигляд: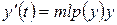 , (8.50)
, (8.50) , і це рівняння описує зростаючу функцію
, і це рівняння описує зростаючу функцію 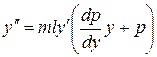 .
.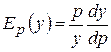 . Тоді вираз для
. Тоді вираз для 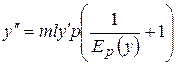
 рівносильна рівності
рівносильна рівності  .
. або
або  , то
, то  і функція
і функція  , або
, або 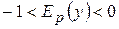 , то
, то  і функція
і функція 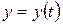 , якщо відомо, що крива попиту
, якщо відомо, що крива попиту  задається рівнянням
задається рівнянням  , норма акселерації
, норма акселерації 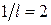 , норма інвестицій
, норма інвестицій  ,
, 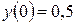 .
.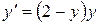 або
або  Виконуючи інтегрування, одержуємо
Виконуючи інтегрування, одержуємо  , або
, або 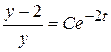 , де
, де 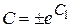 .
. .
.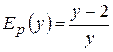 і умова
і умова  , що визначає розташування точки перегину на кривій, дає
, що визначає розташування точки перегину на кривій, дає 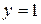 .
.
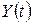 , отриманий на момент часу
, отриманий на момент часу 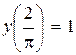 деякою галуззю, є сумою інвестицій
деякою галуззю, є сумою інвестицій  :
: . (8.51)
. (8.51) , 8.52)
, 8.52)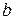 – коефіцієнт капіталоємності приросту прибутку
– коефіцієнт капіталоємності приросту прибутку  (що рівносильне (8.47) при сталій ціні на продукцію
(що рівносильне (8.47) при сталій ціні на продукцію 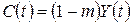 , де
, де 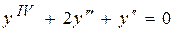 – норма інвестицій. Тоді із (8.51) і (8.52) одержимо
– норма інвестицій. Тоді із (8.51) і (8.52) одержимо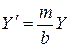 , (8.53)
, (8.53) .
.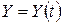 , якщо відомо, що розмір споживання задається функцією
, якщо відомо, що розмір споживання задається функцією 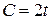 , коефіцієнт капіталоємності приросту прибутку
, коефіцієнт капіталоємності приросту прибутку 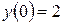 .
.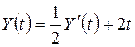 ,
,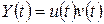 .
.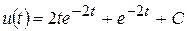 ,
,  . Значення сталої
. Значення сталої 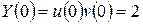 , то
, то 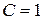 . Остаточно маємо
. Остаточно маємо 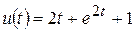 .
.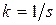 , де
, де 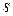 – граничне накопичення. Це припущення можна записати у вигляді рівняння
– граничне накопичення. Це припущення можна записати у вигляді рівняння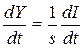 . (8.54)
. (8.54) з коефіцієнтом пропорційності
з коефіцієнтом пропорційності 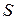 , тобто
, тобто 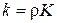 . Диференціюючи по
. Диференціюючи по 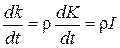 . (8.55)
. (8.55)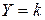 . Диференціюючи по
. Диференціюючи по 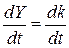 . (8.56)
. (8.56)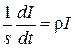 або
або 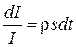 . (8.57)
. (8.57)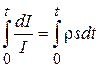 , або
, або 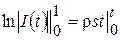 , звідки
, звідки  .
.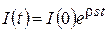 , (8.58)
, (8.58) – це швидкість грошового потоку в початковий момент часу.
– це швидкість грошового потоку в початковий момент часу.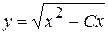 є розв'язком диференціального рівняння
є розв'язком диференціального рівняння  .
. . 8.3.
. 8.3. 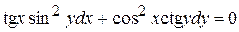 .
.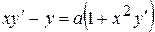 . 8.5.
. 8.5. 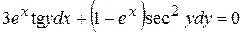 .
. . 8.7.
. 8.7.  .
. .
. . 8.10.
. 8.10. 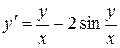 .
.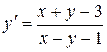 . 8.12.
. 8.12. 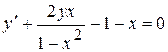 .
.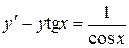 . 8.14.
. 8.14. 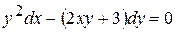 .
. . 8.16.
. 8.16. 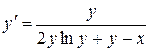 .
. . 8.18.
. 8.18. 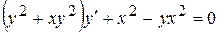 .
. . 8.20.
. 8.20.  .
. . 8.22.
. 8.22.  .
.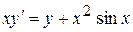 . 8.24.
. 8.24. 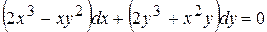 .
. ,
, 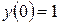 .
. ,
, 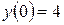 .
. ,
, 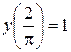 .
.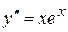 .
.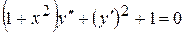 .
. .
.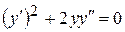 .
. .
. ,
, 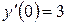 .
. ,
, 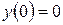 ,
,  .
. . 8.36.
. 8.36. 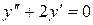 .
.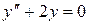 . 8.38.
. 8.38. 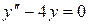 .
.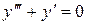 . 8.40.
. 8.40. 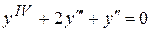 .
. . 8.42.
. 8.42. 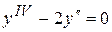 .
.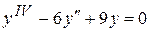 . 8.44.
. 8.44. 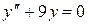 .
. . 8.46.
. 8.46. 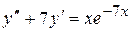 .
.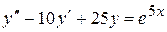 . 8.48.
. 8.48. 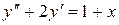 .
. . 8.50.
. 8.50. 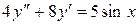 .
. . 8.52.
. 8.52. 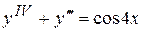 .
.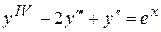 .
.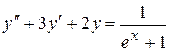 . 8.55.
. 8.55. 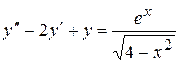 .
.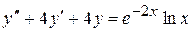 . 8.57.
. 8.57. 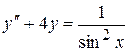 .
. . 8.59.
. 8.59.  .
. . 8.61.
. 8.61. 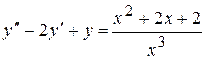 .
. ,
, 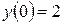 ,
, 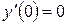 .
.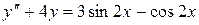 ,
, 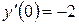 .
. ,
, 


