
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальні рівняння першого порядкуСодержание книги Поиск на нашем сайте Згідно з означенням 8.1 диференціальне рівняння першого порядку має вигляд
Якщо співвідношення (8.2) розв’язати відносно
яке називається диференціальним рівнянням першого порядку, розв’язаним відносно похідної. Таке рівняння завжди можна записати в диференціальній формі
Дійсно, якщо Навпаки, якщо диференціальне рівняння записане у формі (8.4), і якщо
тобто записати у вигляді Диференціальне рівняння першого порядку має, взагалі, не один, а незліченну множину розв'язків. Так, для рівняння Розв'язок диференціального рівняння Графіком частинного розв'язку диференціального рівняння є інтегральна крива, графіком загального розв'язку – сім’я інтегральних кривих. На рис. 8.1 зображена сім’я інтегральних кривих диференціального рівняння
Для того, щоб із загального розв'язку виділити визначений частинний розв'язок, приходиться задавати значення шуканої функції Відшукання розв'язку диференціального рівняння Теорема Коші. Якщо функція Геометрично це твердження означає, що через кожну внутрішню точку Будемо розглядати, як правило, диференціальні рівняння, для яких умови теореми Коші виконуються. Не існує загального методу розв'язання диференціальних рівнянь першого порядку. Розглянемо лише деякі типи рівнянь, для кожного з яких існує свій метод розв'язання.
Диференціальні рівняння першого порядку З подільними змінними.
Розглянемо рівняння вигляду
яке називається рівнянням з розділеними змінними. Дане рівняння є рівністю двох диференціалів деяких функцій, з чого випливає, що функції або рівні, або розрізняються на довільну сталу. Розв'язок рівняння одержимо, проінтегрувавши рівність
Рівняння з подільними змінними має вигляд
Розділимо змінні, тобто перетворимо рівняння так, щоб біля диференціала
Проінтегрувавши, прийдемо до розв'язку у вигляді
Рівняння
Рівнянням такого типу є рівняння
Запишемо довільну сталу у вигляді
Звідки Розв’яжемо диференціальне рівняння
де шукана функція Розділимо змінні, одержимо Обчислимо значення довільної сталої, виходячи з початкових умов. Отже формула для визначення чисельності населення має такий вигляд:
де Наприклад, якщо в деякий державі чисельність населення на даний момент часу 100 млн осіб, коефіцієнт природного приросту Приклад 8.1. Знайти частинний розв'язок диференціального рівняння Розв’язання. Дане рівняння є рівнянням з подільними змінними. Поділимо ліву і праву частину рівності на
|
|||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

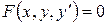 . (8.2)
. (8.2) , то одержимо рівняння вигляду
, то одержимо рівняння вигляду , (8.3)
, (8.3)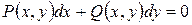 . (8.4)
. (8.4) , а це означає, що
, а це означає, що  .
. , то його завжди можна розв’язати щодо похідної:
, то його завжди можна розв’язати щодо похідної: ,
, розв'язками є функції
розв'язками є функції 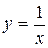 ,
,  ,
,  і, взагалі,
і, взагалі, 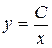 , де
, де  – довільна стала. У цьому легко переконатися, підставивши потрібне значення
– довільна стала. У цьому легко переконатися, підставивши потрібне значення 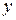 і значення похідної
і значення похідної  , що містить у собі довільну сталу, будемо називати загальним розв'язком диференціального рівняння. Загальний розв'язок, не розв’язаний щодо шуканої функції
, що містить у собі довільну сталу, будемо називати загальним розв'язком диференціального рівняння. Загальний розв'язок, не розв’язаний щодо шуканої функції  Рис. 8.1.
Рис. 8.1.
 при деякому значенні аргументу
при деякому значенні аргументу  . Пари чисел
. Пари чисел  – “початкової точки” на площині
– “початкової точки” на площині 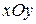 . Будемо казати, що розв'язок
. Будемо казати, що розв'язок 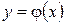 рівняння
рівняння  , тобто, якщо графік проходить через точку
, тобто, якщо графік проходить через точку  .
.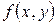 неперервна в деякій області
неперервна в деякій області 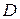 площини
площини  , то яка б не була точка
, то яка б не була точка  значення
значення 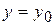 .
. неперервна для всіх
неперервна для всіх 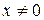 , її частинна похідна
, її частинна похідна  також неперервна для усіх
також неперервна для усіх  , (8.5)
, (8.5) .
.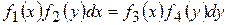 . (8.6)
. (8.6)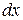 стояла множником функція аргументу
стояла множником функція аргументу 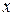 , а біля диференціала
, а біля диференціала 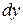 відповідно функція аргументу
відповідно функція аргументу  , одержимо рівняння з розділеними змінними
, одержимо рівняння з розділеними змінними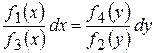 .
.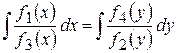 .
. , тоді замінивши
, тоді замінивши  і, помноживши рівняння на
і, помноживши рівняння на 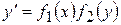 ,
, 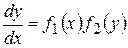 ,
,  ,
, 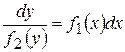 ,
, 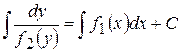 .
.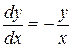 ,
,  ,
,  .
. , що не змінить її змісту, тоді
, що не змінить її змісту, тоді .
.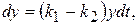
 .
. . Проінтегрувавши, знайдемо, що
. Проінтегрувавши, знайдемо, що  ,
, 
 і, остаточно,
і, остаточно, 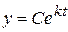 – загальний розв'язок диференціального рівняння.
– загальний розв'язок диференціального рівняння.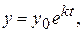
 – коефіцієнт природного приросту;
– коефіцієнт природного приросту; 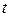 – число років.
– число років. , то через 5 років чисельність населення цієї держави буде дорівнювати:
, то через 5 років чисельність населення цієї держави буде дорівнювати: 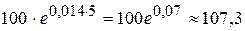 млн осіб.
млн осіб.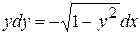 , що задовольняє початковій умові
, що задовольняє початковій умові  .
.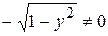 , одержимо:
, одержимо: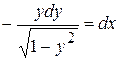 ,
, 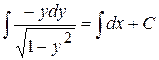 ,
, 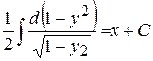 , або
, або 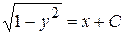 . Звідки
. Звідки  – інтеграл диференціального рівняння. Графіком інтеграла даного диференціального рівняння є сім’я кіл з центром у точці
– інтеграл диференціального рівняння. Графіком інтеграла даного диференціального рівняння є сім’я кіл з центром у точці  на вісі абсцис і радіусом
на вісі абсцис і радіусом 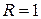 . Надаючи
. Надаючи 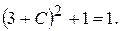 Звідки
Звідки 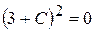 , або
, або 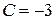 . Отже, частинним розв'язком рівняння є функція
. Отже, частинним розв'язком рівняння є функція  .
.


