
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системи диференціальних рівнянь ⇐ ПредыдущаяСтр 5 из 5
Системою двох диференціальних рівнянь першого порядку називається сукупність співвідношень
де Розв'язком системи (8.40) називається всяка пара функцій Система диференціальних рівнянь першого порядку, розв’язаних відносно похідних від невідомих функцій, називається нормальною системою диференціальних рівнянь. Загальний вигляд нормальної системи двох диференціальних рівнянь із двома невідомими функціями
Від системи двох диференціальних рівнянь завжди можна перейти до одного рівняння з однією невідомою функцією, наприклад Приклад 8.16. Розв’язати систему рівнянь
Розв’язання. Продиференціюємо перше рівняння за
Замінивши Підставляючи замість Знайдемо його розв'язок згідно з
Обчислимо похідні
Підставляючи Підставляючи знайдене значення
або Сім’я розв'язків даної системи рівнянь дається функціями
Системи лінійних однорідних диференціальних рівнянь Зі сталими коефіцієнтами.
Система двох лінійних однорідних диференціальних рівнянь зі сталими коефіцієнтами має вигляд
Розв'язки цієї системи мають такі властивості. 1. Якщо 2. Якщо З властивостей 1 і 2 випливає, що для будь-яких чисел Будемо шукати ненульові розв'язки системи (8.42) у вигляді
де Підставляючи функції (8.43) та їх похідні в рівняння системи (8.42) після скорочення на
Для того, щоб ця система рівнянь мала ненульовий розв'язок, необхідно і достатньо, щоб визначник системи дорівнював нулю. Таким чином число k повинно задовольняти рівняння
Рівняння (8.45) називається характеристичним рівнянням системи (8.42). Це рівняння другого степеня відносно Позначимо ці розв'язки відповідно Лінійна комбінація цих розв'язків з довільними коефіцієнтами
також буде розв'язком системи (8.42). Якщо корені характеристичного рівняння (8.45) різні, то можна показати, що цей розв'язок буде загальним розв'язком системи (8.42). У випадку, якщо корені характеристичного рівняння комплексно-спряжені: У випадку кратних коренів характеристичного рівняння відшукання загального розв'язку системи (8.42) значно складніше. Приклад 8.17. Розв’язати систему рівнянь
Розв’язання. Характеристичне рівняння матриці системи має вигляд Після перетворень одержуємо два різних дійсних корені рівняння
При
Очевидно, що система має незліченну множину розв'язків, яку можна виразити залежністю
Аналогічно попередня система має незліченну множину розв'язків, яку можна виразити залежністю Отже, загальний розв'язок заданої системи рівнянь:
Задачі економічної динаміки Диференціальні рівняння знаходять достатньо широке застосування в моделях економічної динаміки, в яких відображується не тільки залежність змінних від часу, але й їх взаємозв’язок у часі. Розглянемо деякі (прості) задачі макроекономічної динаміки. Нехай Позначимо через
Тут знехтуємо часом між закінченням виробництва продукції та її реалізацією, тобто вважаємо, що інвестиційний лаг дорівнює нулю. Вважаючи, що розмір інвестицій
де коефіцієнт пропорційності Підставляючи останній вираз (8.48) для
де Отримано диференціальне рівняння – з подільними змінними. Розв’язуючи його, приходимо до функції Зазначимо, що рівняння (8.49) описує також зростання народонаселення (демографічний процес), динаміку росту цін при сталій інфляції, процес радіоактивного розпаду та ін. На практиці умова насиченості ринку може бути прийнятною тільки для достатньо вузького часового інтервалу. В загальному випадку крива попиту, тобто залежність ціни
залишаючись як і раніше рівнянням з подільними змінними. Оскільки всі співмножники у правій частині рівняння додатні, то
Нагадаємо, що еластичність попиту (відносно ціни) визначається формулою
і умова Таким чином, якщо попит еластичний, тобто Приклад 8.18. Знайти вираз для обсягу реалізованої продукції Розв’язання. Рівняння (8.50) в цьому випадку приймає такий вигляд: Враховуючи, що Графік даної функції схематично зображений на рис. 8.2. У даному випадку еластичність попиту задається функцією
Рис. 8.2. Крива, зображена на рис. 8.4, називається логістичною. Подібні криві описують процес розповсюдження інформації (реклами), динаміку епідемій, процес розмноження бактерій в обмеженому середовищі та ін. Розглянемо тепер іншу задачу. Прибуток
Як і раніше в моделі природного росту, будемо вважати, що швидкість збільшення прибутку пропорційна розміру інвестицій, тобто справедлива рівність
де Розглянемо поведінку функції прибутку Нехай
що рівносильне рівнянню (8.49) при В ряді випадків тип функції споживання Приклад 8.19. Знайти функцію прибутку Розв’язання. Із співвідношень (8.51) і (8.52) маємо рівняння
тобто функція прибутку задовольняє лінійне неоднорідне рівняння першого порядку. Будемо шукати розв’язок у вигляді Тоді маємо Розглянемо економічну модель Е.Д. Домара. Основні припущення цієї моделі такі: 1. Будь-яка зміна швидкості грошового потоку 2. Швидкість зміни попиту
3. Економічний потенціал
В моделі Домара передбачається, що весь економічний потенціал повністю використовується, тобто
Підставляючи (8.54) та (8.55) в (8.56), маємо
Щоб знайти функцію
Потенціюючи останню рівність, одержуємо остаточний вираз для
де Таким чином, для того, щоб підтримувати рівновагу між обсягом вироблених благ та сукупним попитом на них, швидкість грошового потоку повинна зростати з експоненціальною швидкістю, згідно з формулою (8.58).
Модель Домара – це типовий приклад моделі зростання, що записується у вигляді одного або декількох диференціальних рівнянь.
Вправи 8.1. Показати, що функція 8.2–8.24. Знайти загальний розв'язок диференціальних рівнянь першого порядку. 8.2. 8.4. 8.6. 8.8. 8.9. 8.11. 8.13. 8.15. 8.17. 8.19. 8.21. 8.23. 8.25–8.27. Знайти частинні розв'язки диференціальних рівнянь першого порядку, що задовольняють заданим початковим умовам. 8.25. 8.26. 8.27. 8.28–8.32. Знайти загальні розв'язки диференціальних рівнянь другого порядку, що допускають зниження порядку. 8.28. 8.29. 8.30. 8.31. 8.32. 8.33–8.34. Знайти частинні розв'язки диференціальних рівнянь другого порядку, які допускають зниження порядку та задовольняють заданим початковим умовам. 8.33. 8.34. 8.35–8.44. Знайти загальні розв'язки лінійних однорідних диференціальних рівнянь другого порядку. 8.35. 8.37. 8.39. 8.41.. 8.43. 8.45–8.53. Знайти загальні розв'язки лінійних неоднорідних диференціальних рівнянь. 8.45. 8.47. 8.49. 8.51. 8.53. 8.54–8.61. Знайти загальні розв'язки лінійних неоднорідних диференціальних рівнянь методом варіації довільних сталих. 8.54. 8.56. 8.58. 8.60. 8.62–8.64. Знайти частинні розв'язки лінійних диференціальних рівнянь другого порядку, що задовольняють заданим початковим умовам. 8.62. 8.63. 8.64. 8.65–8.72. Розв’язати системи диференціальних рівнянь. 8.65. 8.67. 8.69. 8.71. 8.73. Нехай попит та пропозиція на товар визначаються відповідно співвідношеннями 8.74. Нехай попит та пропозиція на товар визначаються співвідношеннями 8.75. Через який проміжок часу відбудеться подвоєння сукупного суспільного продукту 8.76. Проінтегрувати диференціальне рівняння розширеного виробництва 8.77. Нехай еластичність виробничої функції 8.78. Нехай еластичність виробничої функції а) б) в) Знайти цю функцію. 8.79. Знайти вираз обсягу реалізованої продукції
Відповіді до вправ Розділ 1 1.
Розділ 2
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.174 (0.135 с.) |
 (8.40)
(8.40)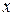 – незалежна змінна, а
– незалежна змінна, а  ,
, 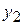 – шукані функції.
– шукані функції. (8.41)
(8.41)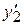 . Після інтегрування одержуємо загальний розв'язок
. Після інтегрування одержуємо загальний розв'язок  , з якого
, з якого 
 .
. його значенням із другого рівняння системи, одержимо
його значенням із другого рівняння системи, одержимо 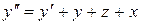 .
. з першого рівняння системи
з першого рівняння системи  , маємо лінійне неоднорідне диференціальне рівняння другого порядку
, маємо лінійне неоднорідне диференціальне рівняння другого порядку  .
. . Однорідне рівняння, що відповідає даному, має вигляд
. Однорідне рівняння, що відповідає даному, має вигляд 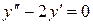 . Його характеристичне рівняння
. Його характеристичне рівняння  має корені
має корені 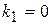 ,
,  . Загальний розв'язок однорідного рівняння буде
. Загальний розв'язок однорідного рівняння буде  . Функція правої частини рівняння
. Функція правої частини рівняння  (неповний многочлен першого порядку). Для неї число
(неповний многочлен першого порядку). Для неї число 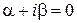 (немає ні показникової, ні тригонометричних функцій) зустрічається серед коренів характеристичного рівняння один раз, тому частинний розв'язок рівняння
(немає ні показникової, ні тригонометричних функцій) зустрічається серед коренів характеристичного рівняння один раз, тому частинний розв'язок рівняння  знайдемо у вигляді
знайдемо у вигляді .
.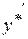 ,
,  :
: ;
; 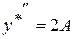 .
. . Прирівнявши коефіцієнти при
. Прирівнявши коефіцієнти при  ,
,  ,
,  ,
,  .
.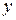 та його похідну
та його похідну 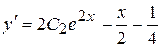 в перше рівняння системи, знаходимо
в перше рівняння системи, знаходимо
 .
.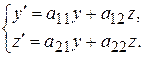 (8.42)
(8.42)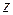 – розв'язки системи (8.42), то
– розв'язки системи (8.42), то  ,
, 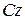 – де
– де  – будь-яке число, також є розв'язками системи.
– будь-яке число, також є розв'язками системи.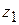 і
і 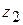 – розв'язки системи (8.42), то функції
– розв'язки системи (8.42), то функції  ,
, 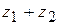 також будуть розв'язками системи.
також будуть розв'язками системи. ,
,  лінійна комбінація розв'язків
лінійна комбінація розв'язків 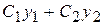 ,
, 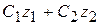 також є розв'язком системи.
також є розв'язком системи.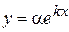 ,
, 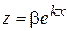 , (8.43)
, (8.43)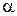 ,
, 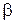 ,
,  – деякі невідомі поки числа, які треба підбирати так, щоб функції (8.43) задовольняли систему (8.42).
– деякі невідомі поки числа, які треба підбирати так, щоб функції (8.43) задовольняли систему (8.42). і перенесення всіх членів в одну частину рівності, одержуємо
і перенесення всіх членів в одну частину рівності, одержуємо (8.44)
(8.44)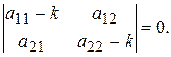 (8.45)
(8.45) і
і 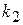 . Кожному з цих коренів відповідає ненульовий розв'язок системи (8.44).
. Кожному з цих коренів відповідає ненульовий розв'язок системи (8.44). ,
,  ,
, 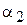 ,
,  . Тоді ненульові розв'язки даної системи диференціальних рівнянь (8.42) матимуть вигляд:
. Тоді ненульові розв'язки даної системи диференціальних рівнянь (8.42) матимуть вигляд: 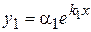 ,
, 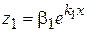 ,
, 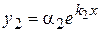 ,
,  .
.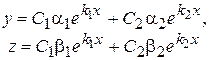 (8.46)
(8.46)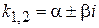 , то знайдені зазначеним вище методом комплексні розв'язки можна замінити дійсними розв'язками, відокремлюючи дійсні і уявні частини їх складовими функціями.
, то знайдені зазначеним вище методом комплексні розв'язки можна замінити дійсними розв'язками, відокремлюючи дійсні і уявні частини їх складовими функціями.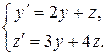
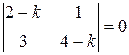 . Звідки
. Звідки 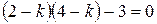 .
. ,
, 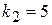 . Отже, загальний розв'язок заданої системи рівнянь має вигляд (8.46):
. Отже, загальний розв'язок заданої системи рівнянь має вигляд (8.46):
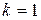 система (8.44) для визначення чисел
система (8.44) для визначення чисел 
 . Приймаючи для конкретності
. Приймаючи для конкретності 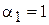 , одержуємо
, одержуємо  . При
. При 
 , Приймаючи
, Приймаючи 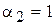 , одержимо
, одержимо 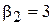 .
.
 – обсяг продукції деякої галуззі, яка реалізована на момент часу
– обсяг продукції деякої галуззі, яка реалізована на момент часу 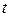 . Будемо вважати, що вся вироблена галуззю продукція реалізується за деякою фіксованою ціною
. Будемо вважати, що вся вироблена галуззю продукція реалізується за деякою фіксованою ціною 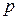 , тобто виконана умова ненасиченості ринку. Тоді доход на момент часу
, тобто виконана умова ненасиченості ринку. Тоді доход на момент часу 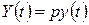 .
.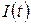 розмір інвестицій, що направляються на розширення виробництва. В моделі природного росту вважають, що швидкість випуску продукції (акселерація) пропорційна величині інвестицій, тобто
розмір інвестицій, що направляються на розширення виробництва. В моделі природного росту вважають, що швидкість випуску продукції (акселерація) пропорційна величині інвестицій, тобто . (8.47)
. (8.47) , (8.48)
, (8.48) (так звана норма інвестицій) – стала величина,
(так звана норма інвестицій) – стала величина, 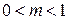 .
.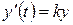 , (8.49)
, (8.49)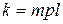 .
.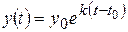 , де
, де 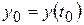 .
.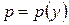 (зі збільшенням обсягу виробленої продукції її ціна падає внаслідок насиченості ринку). Тому модель зростання за умов конкурентного ринку приймає такий вигляд:
(зі збільшенням обсягу виробленої продукції її ціна падає внаслідок насиченості ринку). Тому модель зростання за умов конкурентного ринку приймає такий вигляд: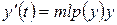 , (8.50)
, (8.50) , і це рівняння описує зростаючу функцію
, і це рівняння описує зростаючу функцію 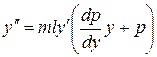 .
.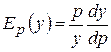 . Тоді вираз для
. Тоді вираз для  можна записати у вигляді
можна записати у вигляді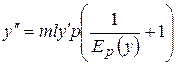
 рівносильна рівності
рівносильна рівності  .
. або
або  , то
, то  і функція
і функція  , або
, або 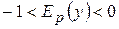 , то
, то  і функція
і функція 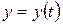 , якщо відомо, що крива попиту
, якщо відомо, що крива попиту  задається рівнянням
задається рівнянням  , норма акселерації
, норма акселерації 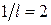 , норма інвестицій
, норма інвестицій  ,
, 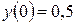 .
.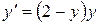 або
або  Виконуючи інтегрування, одержуємо
Виконуючи інтегрування, одержуємо  , або
, або 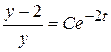 , де
, де 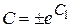 .
.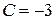 . Виражаючи
. Виражаючи  .
.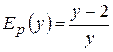 і умова
і умова  , що визначає розташування точки перегину на кривій, дає
, що визначає розташування точки перегину на кривій, дає 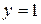 .
.
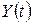 , отриманий на момент часу
, отриманий на момент часу 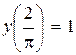 деякою галуззю, є сумою інвестицій
деякою галуззю, є сумою інвестицій  :
: . (8.51)
. (8.51) , 8.52)
, 8.52)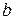 – коефіцієнт капіталоємності приросту прибутку
– коефіцієнт капіталоємності приросту прибутку  (що рівносильне (8.47) при сталій ціні на продукцію
(що рівносильне (8.47) при сталій ціні на продукцію 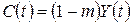 , де
, де 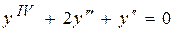 – норма інвестицій. Тоді із (8.51) і (8.52) одержимо
– норма інвестицій. Тоді із (8.51) і (8.52) одержимо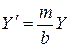 , (8.53)
, (8.53) .
.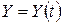 , якщо відомо, що розмір споживання задається функцією
, якщо відомо, що розмір споживання задається функцією 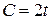 , коефіцієнт капіталоємності приросту прибутку
, коефіцієнт капіталоємності приросту прибутку 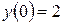 .
.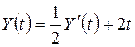 ,
,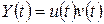 .
.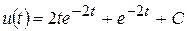 ,
,  . Значення сталої
. Значення сталої 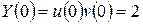 , то
, то 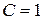 . Остаточно маємо
. Остаточно маємо 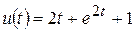 .
.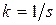 , де
, де 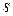 – граничне накопичення. Це припущення можна записати у вигляді рівняння
– граничне накопичення. Це припущення можна записати у вигляді рівняння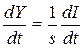 . (8.54)
. (8.54) з коефіцієнтом пропорційності
з коефіцієнтом пропорційності 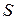 , тобто
, тобто 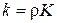 . Диференціюючи по
. Диференціюючи по 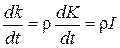 . (8.55)
. (8.55)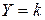 . Диференціюючи по
. Диференціюючи по 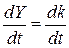 . (8.56)
. (8.56)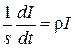 або
або 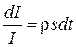 . (8.57)
. (8.57)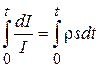 , або
, або 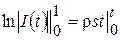 , звідки
, звідки  .
.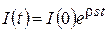 , (8.58)
, (8.58) – це швидкість грошового потоку в початковий момент часу.
– це швидкість грошового потоку в початковий момент часу.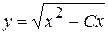 є розв'язком диференціального рівняння
є розв'язком диференціального рівняння  .
. . 8.3.
. 8.3. 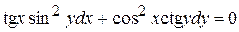 .
.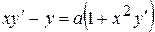 . 8.5.
. 8.5. 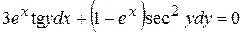 .
. . 8.7.
. 8.7.  .
. .
. . 8.10.
. 8.10. 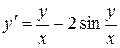 .
.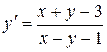 . 8.12.
. 8.12. 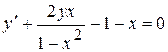 .
.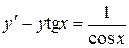 . 8.14.
. 8.14. 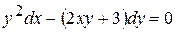 .
. . 8.16.
. 8.16. 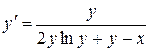 .
. . 8.18.
. 8.18. 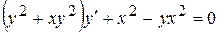 .
. . 8.20.
. 8.20.  .
. . 8.22.
. 8.22.  .
.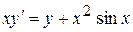 . 8.24.
. 8.24. 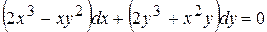 .
. ,
, 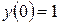 .
. ,
, 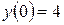 .
. ,
, 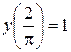 .
.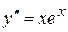 .
.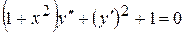 .
. .
.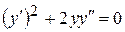 .
. .
. ,
, 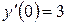 .
. ,
, 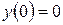 ,
,  .
. . 8.36.
. 8.36. 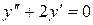 .
.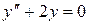 . 8.38.
. 8.38. 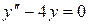 .
.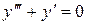 . 8.40.
. 8.40. 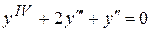 .
. . 8.42.
. 8.42. 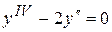 .
.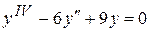 . 8.44.
. 8.44. 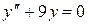 .
. . 8.46.
. 8.46. 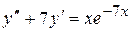 .
.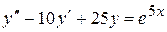 . 8.48.
. 8.48. 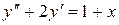 .
. . 8.50.
. 8.50. 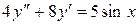 .
. . 8.52.
. 8.52. 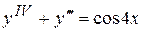 .
.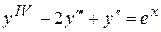 .
.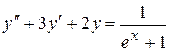 . 8.55.
. 8.55. 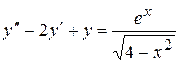 .
.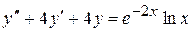 . 8.57.
. 8.57. 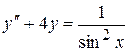 .
. . 8.59.
. 8.59.  .
. . 8.61.
. 8.61. 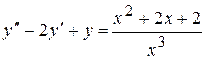 .
. ,
, 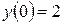 ,
, 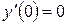 .
.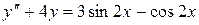 ,
, 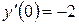 .
. ,
,  8.66.
8.66. 
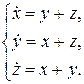 8.68.
8.68. 
 8.70.
8.70. 
 8.72.
8.72. 
 ,
,  , де
, де  – тенденція формування ціни (похідна ціни за часом). Нехай також в початковий момент часу ціна за одиницю товару складала 1 грош. од. Виходячи з потреб відповідності попиту пропозиції, знайти закон зміни ціни в залежності від часу.
– тенденція формування ціни (похідна ціни за часом). Нехай також в початковий момент часу ціна за одиницю товару складала 1 грош. од. Виходячи з потреб відповідності попиту пропозиції, знайти закон зміни ціни в залежності від часу.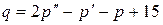 . Нехай також в початковий момент часу
. Нехай також в початковий момент часу  ,
,  . Виходячи з потреб відповідності попиту пропозиції, знайти залежність ціни від часу.
. Виходячи з потреб відповідності попиту пропозиції, знайти залежність ціни від часу. , де
, де  ,
,  ,
,  .
. , вважаючи, що
, вважаючи, що  ,
,  – сталі.
– сталі.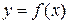 відносно змінної
відносно змінної  . Визначити саму функцію, якщо її графік проходить через точку
. Визначити саму функцію, якщо її графік проходить через точку 
 .
. відносно змінної
відносно змінної  ,
,  ;
; ;
; .
.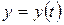 та її значення при
та її значення при 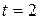 , якщо відомо, що крива попиту має вигляд
, якщо відомо, що крива попиту має вигляд  , норма акселерації
, норма акселерації  , норма інвестицій
, норма інвестицій  ,
, 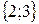 ,
,  ,
,  ,
,  ,
,  ,
,  . 4. а)
. 4. а)  ; б)
; б)  ; в)
; в) 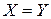 ; г)
; г)  ,
,  ; б)
; б)  ,
,  ; в)
; в) 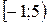 ,
,  . 7. а)
. 7. а)  ; б)
; б)  ; в)
; в)  ; в)
; в)  ,
,  ; г) 1, 0.
; г) 1, 0.


