
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування рівнянь. Властивості рівняньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розв’язування будь-якого рівняння зводиться до виконання певних перетворень, у результаті яких дане рівняння замінюють більш простим. Розв’яжемо, наприклад, рівняння:
1. Розкриємо дужки: 5 х - 10 + 11 = 3 х + 9. (2) 2. Зведемо подібні доданки в лівій частині рівняння: 5 х + 1 = 3 х + 9. (3) 3. Перенесемо доданки зі змінною х у ліву частину рівняння, а без змінної — у праву, змінивши їхні знаки на протилежні: 5 х - 3 х = 9 - 1. (4) 4. Зведемо подібні доданки у кожній частині рівняння: 2 х = 8. (5) 5. Поділимо обидві частини рівняння на 2: х = 4. Отже, рівняння (1) має єдиний корінь — число 4. Розв’язуючи рівняння (1), ми виконували певні перетворення: розкривали дужки, зводили подібні доданки, переносили доданки з однієї частини рівняння в іншу, ділили обидві частини рівняння на число. Із цими перетвореннями пов’язані такі основні властивості рівнянь: Властивість 1. У будь-якій частині рівняння можна розкрити дужки або звести подібні доданки. Властивість 2. Будь-який доданок можна перенести з однієї частини рівняння в іншу, змінивши його знак на протилежний. Властивість 3. Обидві частини рівняння можна помножити або поділити на одне і те ж, відмінне від нуля, число. Якщо в деякому рівнянні виконати одне з перетворень, вказаних у властивостях 1, 2 або 3, то одержимо рівняння, яке має ті ж корені, що й початкове рівняння. Розв’язуючи рівняння (1), ми послідовно одержували рівняння (2),
Властивості рівнянь можна обґрунтувати, використовуючи такі властивості числових рівностей: Якщо a = b ¾ правильна числова рівність і с ¾ деяке число, то:
З першої властивості числових рівностей можна одержати такий наслідок: якщо з однієї частини правильної числової рівності перенести в іншу частину доданок, змінивши його знак на протилежний, то одержимо правильну числову рівність. Використовуючи властивості числових рівностей, доведемо, наприклад, що 3 х = х + 2 (6) має ті ж корені, що й рівняння 3 х - х = 2. (7) (Це властивість 2 для рівняння 3 х = х + 2.) ● Нехай х = a ¾ довільний корінь рівняння (6). Тоді 3 а = а + 2 ¾ правильна числова рівність. Перенесемо доданок a в ліву частину рівності, змінивши його знак на протилежний. Одержимо правильну числову рівність 3 а - а = 2, з якої випливає, що х = a є коренем рівняння (7). Ми довели, що довільний корінь рівняння (6) є коренем рівняння (7). Навпаки, нехай х = b ¾ довільний корінь рівняння (7). Тоді числова рівність 3 b - b = 2 є правильною. Перенесемо доданок - b у праву частину рівності, змінивши його знак на протилежний. Одержимо правильну числову рівність 3 b = b + 2, з якої випливає, що х = b є коренем рівняння (6). Ми довели, що довільний корінь рівняння (7) є коренем рівняння (6). Отже, рівняння (6) і (7) мають одні й ті ж корені. ●
Приклад 1. Розв’язати рівняння ● Помноживши обидві частини рівняння на 14, матимемо:
2 х - 3 х = -31 + 16; - х = -15; х = 15. Відповідь. 15. ● Приклад 2. Розв’язати рівняння 25(z - 3) + 100 z = 125. ● Поділивши обидві частини рівняння на 25, матимемо: z - 3 + 4 z = 5; 5 z = 5 + 3; 5 z = 8; z = 1,6. Відповідь. 1,6. ● Усно 23. Назвіть властивість рівнянь, на основі якої здійснено перехід від першого рівняння до другого: а) 2 х - 5 = 1; 2 х = 1 + 5; б) 3 х + 2 = 5 х + 4; 3 х - 5 х = 4 - 2; в) 2(х - 2) = х; 2 х - 4 = х; г) 24. Обидві частини рівняння х (х - 1) = 2 х поділили на х й одержали рівняння х - 1 = 2. Чи мають ці рівняння одні й ті ж корені? Чи можна, розв’язуючи рівняння х (х - 1) = 2 х, ділити обидві його частини на х? 25. Поясніть кожний крок розв’язання рівняння:
Розв’яжіть рівняння: 26. а) 7 х - 4 = 3 х - 9; б) 2 х + 3(х + 1) = 8. 27. а) 8 х + 4 = 3 х + 4; б) 4(х – 3) = х. 28. а) 30(х + 2) = 15(х - 2); б) 200(х – 1) = 300. 29. а) 161(2 х + 2) = 161 х; б) 50(х + 3)= 250(х + 1). 30. а) 31. а)
Розв’яжіть рівняння: 32. а) 200(х - 5) = 100(х + 1) + 500; б) 350 х + 250(5 х - 4) - 800 = 0; в) 33. а) 210(х - 12) + 140(х + 18) = 70; б) 34. а) 35. а)
36. Розв’яжіть рівняння: а) (х + 1)(х + 2)(х + 3)(х + 4) = (х + 1)(х + 2)(х + 3)(х + 5); б) Вправи для повторення 37. Знайдіть значення виразу: а) 2(а + 1) - 4(а - 2), якщо а = -0,1; б) 1,4 x - (1+ 0,7 x) - (3,3 х - 2), якщо х = 2,25; в) -2(а + b - 2) - a + 2 b - 4, якщо а = 3; b = -1. 38. У сьомих класах навчається 84 учні, що становить 39. У місті зараз проживає 52 000 жителів. Відомо, що населення цього а) Скільки жителів буде в місті через рік? б) Скільки жителів було в місті рік тому?
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.19 (0.008 с.) |

 (1)
(1) Для тих, хто хоче знати більше
Для тих, хто хоче знати більше Приклади розв’язання вправ
Приклади розв’язання вправ
 2(х - 8) = 3 х - 31; 2 х - 16 = 3 х - 31;
2(х - 8) = 3 х - 31; 2 х - 16 = 3 х - 31; = х; 1 - 4 х = 3 х.
= х; 1 - 4 х = 3 х.
 1 + 2 х = 12 + 3 х
2 х - 3 х = 12 - 1
- х = 11
х = -11.
1 + 2 х = 12 + 3 х
2 х - 3 х = 12 - 1
- х = 11
х = -11.
 Рівень А
Рівень А б)
б)  (х + 1) =
(х + 1) =  ; в)
; в) 
 б)
б)  (х - 5) = 1; в)
(х - 5) = 1; в) 
 Рівень Б
Рівень Б ; г)
; г) 

 б)
б) 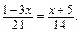
 б)
б) 
 Рівень В
Рівень В
 усіх учнів школи. Скільки всього учнів у школі?
усіх учнів школи. Скільки всього учнів у школі?


