
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування перетворень виразівСодержание книги
Поиск на нашем сайте Нам уже траплялося чимало завдань, для розв’язання яких треба було перетворювати той чи інший вираз. Здебільшого ми використовували перетворення виразів, коли розв’язували рівняння, доводили тотожності, знаходили значення виразів. Розглянемо ще деякі задачі, пов’язані з перетвореннями виразів. Порівняння значень многочлена з нулем. Приклад 1. Довести, що многочлен х 2 - 8 х + 18 набуває лише додатних значень. ● Виділивши із тричлена х 2 - 8 х + 18 квадрат двочлена, матимемо: х 2 - 8 х + 18 = х 2 - 8 х + 16 – 16 + 18 = (х - 4)2 + 2. Ми подали многочлен у вигляді суми двох доданків (х - 4)2 і 2. Доданок (х - 4)2 для будь-яких х набуває лише невід’ємних значень, доданок 2 — додатний. Тому вираз (х - 4)2 + 2 набуває лише додатних значень. Оскільки х 2 - 8 х + 18 = (х - 4)2 + 2, то й вираз х 2 - 8 х + 18 набуває лише додатних значень. ● Знаходження найбільшого і найменшого значень виразів. Виходячи з рівності х 2 - 8 х + 18 = (х - 4)2 + 2, одержаній у прикладі 1, можна вказати найменше значення многочлена х 2 - 8 х + 18. Воно дорівнює 2, до того ж, цього найменшого значення многочлен набуває, якщо х = 4. Приклад 2. Знайти найбільше значення многочлена - х 2 + 4 х + 1. ● Спочатку даний вираз запишемо так: - х 2 + 4 х + 1 = -(х 2 - 4 х - 1). Тоді:
Найбільше значення многочлена дорівнює 5. ● Розв’язування задач на подільність. Приклад 3. Довести, що для будь-якого цілого значення n значення виразу (2 n + 3)2 - – (2 n - 3)(2 n + 5) ділиться на 8. ● Спростимо даний вираз: (2 n + 3)2 - (2 n - 3)(2 n + 5) = 4 n 2 + 12 n + 9 - (4 n 2 + 10 n - 6 n - 15) = = 4 n 2 + 12 n + 9 - 4 n 2 - 4 n + 15 = 8 n + 24 = 8(n + 3). Для будь-якого цілого значення n добуток 8(n + 3) ділиться на 8, а тому й значення виразу (2 n + 3)2 - (2 n - 3)(2 n + 5) ділиться на 8. ● Знаходження значень многочлена за допомогою мікрокалькулятора. Приклад 4. За допомогою мікрокалькулятора знайти значення многочлена ● Значення даного многочлена шукати зручніше, якщо його попередньо перетворити так: 12 х 3 - 24 х 2 + 15 х - 8 = (12 х 2 - 24 х + 15) х - 8 = ((12 х - 24) х + 15) х - 8. Якщо х = 2,8, то схема обчислень є такою:
Виконавши обчислення, знайдемо значення многочлена. Воно дорівнює 109,264. ● Усно 715. Знайдіть найменше значення виразу: а) x 2 + 7; б) (а - 6)2; в) (b - 1)2 + 3. 716. Знайдіть найбільше значення виразу: a) 7 - х 2; б) 1 - (х - 2)2; в) 5 - (x + 5)2. За якого значення х вираз набуває найбільшого значення?
Доведіть, що вираз набуває лише невід’ємних значень: 717. а) x 2 + 2 x + 1; б) 4 m 2 + 4 mn + n 2 + 3. 718. а) a 2 - 4 а + 4; б) x 2 - 2 xy + y 2 + 4. Доведіть, що значення виразу ділиться на дане число: 719. а) 2452 - 2362 на 9; б) 4382 - 622 на 500; в) 523 - 363 на 16; г) 753 + 253 на 100. 720. а) 8112 - 7122 на 99; б) 483 - 193 на 29. За допомогою мікрокалькулятора знайдіть значення многочлена: 721. а) 4 х 3 - 6 х 2 + 5 х - 3, якщо х = 5; х = 3,2; х = -2,6; б) 1,2 х 3 + 2,4 х 2 + 0,5 х - 1, якщо х = 1,7; в) 4,5 х 4 + 4 х 3 - 3,5 х 2+ 2 х - 1,8, якщо х = 4. 722. а) 15 х 3 - 8 х 2 + 12 х - 30, якщо х = 2; х = 1,2; х = -4; б) 2,4 х 4 - 7,2 х 3 - 3,3 х 2+ 4,5 х, якщо х = 3.
Доведіть, що вираз набуває лише від’ємних значень: 723. а) -(а 2 - 2 а + 4); б) - x 2+ 4 x - 5. 724. а) -(х 2 - 2 х + 2); б) - y 2 + 2 y - 4. Знайдіть найменше значення виразу та значення змінної, для якого вираз набуває найменшого значення: 725. a) x 2 - 4 x + 4; б) х 2 - 4 х + 7. 726. а) a 2 + 6 a + 9; б) x 2 - 6 x + 10. Доведіть, що для будь-якого цілого значення n значення виразу ділиться на дане число: 727. а) (n - 2)2 + 3 n 2 на 4; б) (n - 2)(2 n - 7) - 2 n 2 - 3 на 11. 728.(n + 2)2 - n (n - 2) + 2 на 6. Доведіть, що для будь-якого цілого значення n значення виразу не ділиться на дане число: 729. а) (n - 5)2 + (2 n - 3)(2 n + 8) на 5; б) (n - 3)(n 2 - 3) - (n 3 - 1) на 3. 730.(n + 3)2 - (n - 3)2 + 3 на 12. 731. Доведіть, що значення виразу 533 - 530 ділиться на 124.
732. Знайдіть найбільше значення виразу та значення змінної, для якого вираз набуває найбільшого значення: a) - x 2 + 2 x – 8; б) - а 2 - 4 а + 3. 733. Чи може значення виразу a 2- 4 a + 7 дорівнювати 1? Розв’яжіть рівняння: 734. а) x 2- 7 x + 12 = 0; б) х 2 - х - 12 = 0. 735. а) (x - 1)2 + (x - 3)2 = 0; б) (x 2- 1)2 + (x - 1)4 = 0. 736. Доведіть, що значення виразу ділиться на дане число: а) 310 + 96 на 10; б) 220+ 225 - 222 на 29. 737. Доведіть, що не існує чисел х та у, для яких виконувалася б рівність: а) х 2+ у 2 - 2 x - 2 у + 3 = 0; б) 2 х 2+ 2 у 2 - 2 xу - 2 x - 2 у + 3 = 0. 738. Запишіть число 4 у вигляді суми таких двох доданків, щоб їх добуток був найбільшим. 739. Різниця двох непарних натуральних чисел ділиться на 5. Чи ділиться різниця кубів цих чисел на 10? Вправи для повторення 740. Довжина прямокутника дорівнює n м, а ширина на k м менша. Запишіть у вигляді виразів периметр та площу прямокутника. 741. Турист деяку відстань проплив моторним човном проти течії річки за 1,2 год, а назад повертався плотом протягом 7,2 год. Знайдіть швидкість течії річки, якщо швидкість човна у стоячій воді дорівнює 21 км/год. 742. Поле, площа якого дорівнює 568 га, поділено на 3 ділянки так, що площа третьої ділянки на 52 га менша від суми площ перших двох ділянок, а площа першої ділянки відноситься до площі другої як 2:3. Знайдіть площу кожної ділянки. 743. Для яких значень коефіцієнта а рівняння aх = 3 має єдиний корінь? Чи існує таке значення а, для якого це рівняння не має коренів?
Формули скороченого множення античні математики використовували задовго до нашої ери. На той час формули подавалися не у звичному нам символічному вигляді, а формулювалися словами.
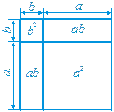
Не важко здогадатися, що йдеться про формулу квадрата суми, яку ми зараз символічно записуємо так: (a + b)2 = a 2 + 2 ab + b 2. Запитання і вправи для повторення § 5 1. Чому дорівнює добуток різниці двох виразів та їх суми? 2. Запишіть і сформулюйте формулу квадрата суми двох виразів; квадрата різниці двох виразів. 3. Чому дорівнює різниця квадратів двох виразів? 4. Наведіть приклад тричлена, який можна записати у вигляді квадрата суми; квадрата різниці. 5. Чому дорівнює сума кубів двох виразів? 6. Чому дорівнює різниця кубів двох виразів? 7. Які способи розкладання многочленів на множники вам відомі? 744. Виконайте множення: а) (5 - a)(5 + a); б) (3 b + 2 a)(3 b - 2 a); в) (х + у 2)(х - у 2); г) (- с + 0,4)(0,4 + с); д) (- m - 5 n)(m - 5 n); е) (ab + 2 a 2)(ab - 2 a 2). 745. Піднесіть до квадрата: а) (а - 2 b)2; б) (3 x + 2 х 2)2; в) (-0,5 ab - 2 c)2. Спростіть вираз: 746. а) (a - 6)(a + 6) + (3 - a)(3+ a); б) (3 x 2 - 1)(3 x 2+ 1) - (1 - 3 x 2)2; в) (5 а - 2 b)2 + (2 а + 5 b)2 - 29 b 2; г) (a - b)2 + (b - c)2 + (c - a)2 - 2(a 2 + b 2 + c 2); д) (a 2 - b 2)(a 2 + b 2)(a 4 + b 4) + a 8 + b 8. 747. Доведіть тотожність: а) (a + b)(a - b) - (a - c)(a + c) = (c - b)(c + b); б) (n + 1)2 + (n + 5)2 - 3 = (n + 2)2 + (n + 4)2 + 3; в) (m - 2)(m + 2)(m 2 + 4)(m 4 + 16) = m 8 - 256. 748. Обчисліть: а) 96 × 104; б) 52 × 48; в) 19,8 × 20,2; г) 7,5 × 8,5. 749. Розв’яжіть рівняння: а) (х - 3)(х + 3) - х (х + 2) = 1; б) (2 х + 5)2 = (2 х - 3)2; в) 750. Доведіть, що для кожного цілого значення n значення виразу: а) (2 n + 1)(2 n - 1) - (n + 1)2 - n - 1 ділиться на 3; б) (2 n + 7)(8 n - 8) - (4 n + 5)2 не ділиться на 6. 751. Доведіть, що значення виразу(k - 2)2 + (k + 2)2 - 2(k - 4)(k + 4) не залежать від значень k. Розкладіть на множники: 752. а) 3 а 2 - 3; б) х 3 - 4 x; в) х 4 у 2 - x 2 у 4; г) 1,44 a 2 - b 4; д) (с 2 + 1)2 - 4 с 2; е) а 2 - 2 ab + b 2 - 1; є) 25 m 2 - (4 m - 4)2; ж) х 2 - у 2 - x - у; з) 2 а 2 - 2 b 2 - (а - b)2. 753. а) а 3 - 64; б) х 3 + 8 z 3; в) (х + 2)3 - у 3. 754. а) а 5 - а 3 + а 2 - 1; б) z 4 + z 3 - 8 z - 8; в) 2 х 4 - 2 x 3 - 2 x + 2. 755*.a) (х 2 + хy + y 2)2- (x 3 - y 3)2; б) x 4+ 4. Розв’яжіть рівняння: 756. а) х 3 - 9 x = 0; б) у (у 2 + 3) = 4 у; в) х 3 - 5 х 2 - x + 5 = 0; г) 2 z 3 + 3 z 2 = 2 z + 3. 757*. а) x 2 - 4 х + 4 + 2(x - 1)2 = 0; б) (x 2+ 1)2 + (x 2 - х)2 = 1; в) | х (х - 1)| + x 2 - 2 х + 1 = 0. Доведіть, що значення виразу ділиться на дане число: 758. а) 4012 - 1992 на 600; б) 853 - 483 на 37; в) 583 + 423 на 100; г) 733 + 731 на 50. 759. а) 825 - 6412 на 7; б) 169 - 328 + 812 на 7. 760. Доведіть, що вираз x 2- 14 x + 50 набуває лише додатних значень. 761. Доведіть, що вираз 4 x - x 2- 5 набуває лише від’ємних значень. 762. Знайдіть найменше значення виразу: а) x 2 + 8 x + 17; б) а 2 - 8 аc + 16 c 2 + 16. 763. Доведіть, що різниця квадратів двох послідовних цілих чисел є непарним числом. 764. Доведіть, що різниця квадратів двох послідовних непарних чисел ділиться на 8. 765*. Доведіть, що значення виразу 1510 - 153 + 2256- 2113 ділиться на 226. 766*. Доведіть, що різниця квадратів двох цілих чисел, які не діляться на 3, кратна 3. 767*. Доведіть, що не існує чисел х та у, для яких виконувалася б рівність: а) х 2+ у 4 - 4 x - 2 у 2 + 7 = 0; б) 2 х 2+ 4 у 2 - 4 xу - 2 x + 3 = 0. Завдання для самоперевірки № 5 Рівень 1. Виконайте множення (a - х)(a + х) і вкажіть правильну відповідь: a) a 2 - 2 ах + х 2; б) a 2 + 2 ах + х 2; в) a 2 + х 2; г) a 2 - х 2. 2. Піднесіть до квадрата (b - 4)2 і вкажіть правильну відповідь: а) b 2 - 4 b + 16; б) b 2 – 16; в) b 2 - 8 b + 16; г) b 2 + 8 b + 16. 3. Розкладіть на множники многочлен у 2 - 9 та вкажіть правильну відповідь: a) (у - 9)(у + 9); б) (у - 3)(у - 3); в) (у - 3)(у + 3); г) (у + 3)(у + 3). 4. Обчисліть 852 – 152 та вкажіть правильну відповідь: а) 140; б) 4900; в) 7000; г) 6125. 5. Подайте тричлен х 2 + 4 х + 4 у вигляді квадрата двочлена та вкажіть правильну відповідь: а) (х - 2)2; б) (х + 4)2; в) (х – 4)2; г) (х + 2)2. 6. Подайте тричлен a 2 - 10 a + 25 у вигляді квадрата двочлена та вкажіть правильну відповідь: а) (а - 10)2; б) (а - 5)2; в) (а - 3)2; г) (а + 5)2. Рівень 1. Спростіть вираз (3 - a)(3+ a) + (1 - a)2 та знайдіть його значення, якщо a = 0,5. 2. Піднесіть до квадрата: а) (4 + 3 b)2; б) (2 a – 5)2. 3. Розв’яжіть рівняння: а) (х – 2)2- x 2 = 12; б) (x + 3)(х – 3) – x 2 = 3 x. 4. Розкладіть на множники: a) 9 у 2 - 16; б) 3 x 2 - 3 y 2; в) 27 a 3- b 3. 5 Подайте у вигляді квадрата двочлена: a) 9 a 2 + 12 a + 4; б) 100 a 2 + b 2 - 20 ab. Рівень 1. Спростіть вираз: а) (2 x - 7 y)2 + (2 x + 7 y)2 - 8 x 2; б) (2 - 3 b 2)(3 b 2 + 2) + (3 b 2 - 1)2. 2. Доведіть тотожність: (a + 1)(a – 1)(a 2 + 1) – (a 2 – 1)2 – 2 a 2 = –2. 3. Розкладіть на множники: а) b 6 - 4 b 4; б) 0,001 a 3- 27 b 3; в) 0,8 a 3 + 0,4 a 2 + 0,4 a 4. 4. Доведіть, що вираз- x 2+ 10 x - 27 набуває лише від’ємних значень. 5. Розв’яжіть рівняння: а) -(2 х + 3)2 + (х + 5)(2 х + 5) = 16; б) x 2- 2 x - 35 = 0. Рівень 1. Спростіть вираз: а) ((x + 2 y 2)(x – 2 y 2))2 + 16 y 8; б) (a + 1)(a – 1)(a 2 + a + 1)(a 2 – a + 1). 2. Розкладіть на множники: а) m 3 - n 3 + 3 m 2 + 3 mn + 3 n 2; б) а 2+ b 2 + c 2 - x 2 + 2 ab + 2 bc + 2 ca. 3. Розв’яжіть рівняння: а) (x 2 - 1)(x 2 + 1)(x 4+ 1) = x 8 + 4 x; б) x 3- 9 = x - 9 x 2. 4. Число n при діленні на 5 дає в остачі 3, а число m ¾ в остачі 4. Доведіть, що число n 2 + m 2 ділиться на 5. 5. Доведіть, що многочлен
ФУНКЦІЇ
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

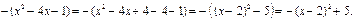
 Рівень А
Рівень А Рівень Б
Рівень Б Рівень В
Рівень В
 г) (5 х + 3)(5 х - 3) +
г) (5 х + 3)(5 х - 3) +  = (5 х - 1)2.
= (5 х - 1)2. набуває лише невід’ємних значень.
набуває лише невід’ємних значень.



