
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множення многочлена на многочленСодержание книги
Поиск на нашем сайте Помножимо многочлен а + b на многочлен c + d. Щоб звести множення цих многочленів до множення многочлена на одночлен, позначимо многочлен c + d через х. Тоді: (a + b)(c + d) = (a + b) x = ax + bx. Повернувшись до заміни х = c + d, матимемо: ax + bx = a (c + d) + b (c + d) = ac + ad + bc + bd. Отже, добутком многочлена а + b і многочлена c + d є многочлен ac + ad + bc + bd: (a + b)(c + d) = ac + ad + bc + bd. Вираз ac + ad + bc + bd ми одержали б одразу, якби помножили a на c і d, потім b на c і d і одержані добутки додали. Можна сказати й так: добуток ac + ad + bc + bd можна одержати, якщо помножити кожний член многочлена a + b на кожний член многочлена с + d й одержані добутки додати. Приходимо до такого правила:
Помножимо за цим правилом многочлен 2 а 2 + b 2 на многочлен 2 а - b: (2 а 2 + b 2)(2 а - b) = 2 a 2 × 2 a + 2 a 2 × (- b) + b 2 × 2 a + b 2 × (- b) = = 4 a 3 - 2 a 2 b + 2 ab 2 - b 3. Виконуючи множення многочленів, проміжні результати можна не записувати: (2 а 2 + b 2)(2 а - b) = 4 a 3 - 2 a 2 b + 2 ab 2 - b 3. У наведених прикладах добуток двох многочленів ми записували у вигляді многочлена. Взагалі, добуток будь-яких многочленів завжди можна записати у вигляді многочлена.
Приклад 1. Виконати множення: а) (2 x 2 - xy + 4 y 2)(2 x - 3 y); б) (a + b)(а + 1)(b - 1). ● а) (2 x 2 - xy + 4 y 2)(2 x - 3 y) = = 4 x 3 - 8 x 2 y + 11 xy 2 - 12 y 3. б) Знайдемо добуток перших двох многочленів, а потім одержаний добуток помножимо на третій многочлен: (a + b)(а + 1)(b - 1) = (a 2+ а + bа + b)(b - 1) = = a 2 b - a 2 + аb - a + b 2 a - ba + b 2 - b = a 2 b - a 2 - a + ab 2+ b 2 - b. ● Приклад 2. Розв’язати рівняння (х - 2)(2 х + 3) - х (2 х + 4) = 3. ● 2 х 2 + 3 х - 4 х - 6- 2 х 2 - 4 x = 3; -5 х - 6 = 3; -5 х = 9; х = -1,8. Відповідь. -1,8. ● Усно 422. Виконайте множення: a) (a + 2)(b + 1); б) (a + b)(c - d); в) (x + y)(a + b - c).
Перемножте многочлени: 423. а) (x + 2)(y + z); б) (b + а)(c - 3); в) (m - 4)(n + k); г) (a - b)(x - y); є) (x + y)(a - 5 b + 2); ж) (2 - c)(a - b - 2); з) (m - n + 1)(k + l). 424. а) (a + b)(c + 3); б) (2 x + y)(3 - 3 z); в) (a - 2 b)(3 х - 4 y); г) (m + n)(a - b + 1); д) (a + b - 2)(с + 5); е) (2 x - y - 1)(a - 3 b). Перетворіть вираз у многочлен стандартного вигляду: 425. a) (a + 3)(4 a - 3); б) (5 b - 4)(3 b - 2); в) (a 2 + 3 a - 4)(3 a - 2); г) (n - m)(n + 4 m); д) (a - 6 b)(2 a - b); е) (4 c - 3 d)(3 c + d). 426. а) (а - 2)(а + 3); б) (3 x + 2)(2 x - 1); в) (a + 5 b)(a - b); г) (4 x - 3 y)(x - 2 y). Спростіть вираз: 427. а) (3 a - 4)(2 a + 1) + 5 a; б) (y + 3)(y - 4) - y (y - 1); в) (2 x - 5)(2 x + 3) - 4(x 2 - x); г) (a 2 + a - 2)(а + 3) + 6 - 4 а 2; д) (a + b)(a - 3 b) + 2 ab; е) (- х + 4 y)(2 x - y) + 2 x 2 - 9 xy. 428. а) (x + 2)(2 x + 3) - 2 x 2; б) (a - 4)(3 a - 4) + 16 a - 16; в) (a + 2 b)(3 а -4 b) + 3 аb - 3 а 2; г) -7 mn + (m + 5 n)(2 m - 3 n). Розв’яжіть рівняння: 429. а) (х - 1)(х + 2) - x 2 = 3; б) (2 y - 1)(2 - y) + 2 y 2 = 1. 430. а) (х + 3)(х - 1) - х 2 = 5; б) 5 х 2 + (1- х)(5 х + 2) = 5.
Перетворіть вираз у многочлен стандартного вигляду: 431. а) (-3 а + 2)(2 а 2 + 2 a - 3); б) (3 x 2- 2 x + 1)(2 x 2+ 5 x); в) (n 2- n + 3)(n 2+ 2 n + 2); г) (2 b 2 - 3 b - 2)(4 b 2+ b - 4); д) (c + 2)(c + 3)(c -5); е) (2 x + 1)(2 x -5)(x 2 + 3 x + 2); є) 432. а) (4 а + 3)(а 2 - 4 a + 2); б) (b 2- 2 b + 3)(3 b 2- 2 b + 1); в) (x - 2)(x + 5)(x - 4); г) (2 y - 3)(y + 2)(4 y 2+ 3 y - 3); д) 433. а) (а + b)(а 2 + 5 ab - b 2); б) (4 x 2- 3 xy + y 2)(2 x - 7 y); в) (3 n 2- 2 nm - m 2)(3 n - 2 m); г) (3 a - 2 b)(а - 2 b)(a 2+ 2 ab). 434. а) (2 x + y)(x 2 + 2 xy - 2 y 2); б) (a - b)(а + 2 b)(3 a - 2 b). Спростіть вираз: 435. а) (3 a - 1)(2 a + 5) + (2 a - 5)(3 a + 1); б) (x + 7)(8 x - 1) - (2 x + 3)(4 x - 1); в) (a - 2)(1 - 2 a + 2 a 2) - 2(a 3 - 3 a 2 - 1); г) (a 2- 2 ab + 4 b 2)(a + 2 b) - a 3 - b 3; д) (3 xy 2 - 7 x 2 y)(3 xy 2 - 2 x 2 y) +(3 xy)3 - (3 xy 2)2. 436. а) (4 x - 3)(3 x + 4) + (2 x - 3)(3 x + 1); б) (2 b - 7)(4 b - 1) - (8 b - 3)(b + 1); в) (x + 3 y)(x 2- 3 xy + 9 y 2) - 18 y 3; г) (a + b)(a + b - 1) - a (a - 1) - b (b - 1). Розв’яжіть рівняння: 437. а) (х - 1)(х - 3) = (х - 2)(х + 3); б) (2 y - 1)(1 - y) + (y + 1)(2 y - 3) = 0; в) (0,5 х - 3,5)(6 х + 2) + 30 х = 3 х (х - 3) - 26; г) 438. а) (х + 6)(х - 4) = (х - 5)(х + 4); б) (0,5 x + 7)(4 x - 1) - (x + 14)(2 x - 1) = 9; в) Доведіть, що значення виразу не залежать від значень х: 439. а) (х + 1)(х + 4) - (х + 2)(х + 3); б) (1 - х)(2 - х)(3 - х) + (x - 4)(x 2- 2 x + 3). 440. (х - 3)(x 2+ 7 x - 3) - (х + 2)(x 2+ 2 x - 28). Доведіть, що для кожного цілого значення k значення виразу: 441. (2 k + 1)(3 k + 2) - (2 k - 1)(3 k - 2) ділиться на 14. 442. (3 k + 2)(4 k - 3) - (2 k + 3)(k - 2) ділиться на 10. 443. Доведіть, що вираз (а 2 + 3)(а 2 - 1) - (а 2 + 4)(а 2 - 2) набуває лише додатних значень. Доведіть тотожність: 444. а) (х + 3)(х 2 - 1) = (х 2 + 2 х - 3)(х + 1); б) (a - b)(b - c)(c - a) = ab (b - a) + bc (c - b) + ca (a - c). 445. а) (а + 2)(а 2 - 2 а - 3) = (а - 3)(а 2 + 3 а + 2); б) (a + b)(b - c) - (a - b)(b + c) = 2(b 2- ac). 446. Знайдіть три послідовних цілих числа, квадрат найменшого з яких на 11 менший від добутку двох інших чисел. 447. Довжина прямокутника в 1,8 разу більша від ширини. Якщо довжину прямокутника збільшити на 3 см, а ширину зменшити на 2 см, то площа зменшиться на 9 см2. Знайдіть довжину і ширину прямокутника. 448.Довжина прямокутника на 4 см більша від ширини. Якщо довжину прямокутника зменшити на 1 см, а ширину збільшити на 2 см, то площа збільшиться на 10 см2. Знайдіть довжину і ширину прямокутника.
449. Спростіть вираз (х - а)(х - b)(х - с)...(х - z), що є добутком 26 множників, у яких від змінної х віднімаються змінні, позначені всіма 26 буквами латинського алфавіту. 450. Спростіть вираз (n ¾ натуральне число): а) (an + bn)(an - bn + 1) - a 2 n + b 2 n ; б) (1 + 2 n + 1)(5- 2 n + 1) + 4 n + 1. 451. Доведіть тотожність: а) (a + b + c)(a 2 + b 2 + c 2 - ab - bc - ca) = a 3 + b 3 + c 3 - 3 abc; б) a 3 + b 3 + c 3 = 3 abc, якщо a + b + c = 0. 452. а) Одне із цілих чисел при діленні на 6 дає в остачі 2, а друге ¾ в остачі 3. Доведіть, що добуток цих чисел ділиться на 6 без остачі. б) Числа a, b і c при діленні на 4 дають відповідно в остачі 1, 2 і 3. Доведіть, що число abc + 2 ділиться на 4 без остачі. 453. Дано чотири послідовних цілих числа. Що більше — добуток найменшого і найбільшого із цих чисел чи добуток інших двох чисел — і на скільки більше? 454. Дві ділянки прямокутної форми мають рівні площі. Довжина другої ділянки на 2 м менша, ніж довжина першої, а ширина другої ділянки на 1 м більша, ніж ширина першої. Доведіть, що довжина першої ділянки удвічі більша від ширини другої. 455. Дано два многочлени: х 4 + 987 х 3 – 876 х 2 + 765 х – 654 і 9876 х 4 – 9800 х 2 – 75. Чому дорівнює сума коефіцієнтів многочлена стандартного вигляду, який є добутком даних многочленів? Вправи для повторення 456. За 2 ручки і 8 зошитів Олег заплатив 4 грн. 20 коп. Скільки коштує ручка, якщо вона на 10 к. дорожча від зошита? 457. Моторний човен проплив 72 км, рухаючись 3 год проти течії річки і 2 год — за течією. Знайдіть швидкість течії річки, якщо швидкість човна у стоячій воді дорівнює 15 км/год. 458. Від пристані А до пристані В катер плив на 20 хв довше, ніж від В до А. Знайдіть відстань між пристанями, якщо швидкість катера у стоячій воді дорівнює 19,2 км/год, а швидкість течії річки — 2,4 км/год. 459. Розв’яжіть рівняння: a) |3 x – 6| = 9; б) 2| x | – 3 = | x |; в) | x - 4| = 3(4 – | x – 4|); г) | x |(| x | – 1) = 2 + | x |2. 460. Обчисліть: а) 37 · 48 + 37 · 52; б) 9,3 · 5,6 – 9,3 · 5,5; в) 1,6 · 8,8 – 3,8 · 1,6. 461. Запишіть одночлен 24 a 3 b 4 у вигляді добутку двох одночленів, одним із яких є: а) 3 a 2 b 2; б) 8 b 3; в) -4 ab 4; г) -12 a 3. 14.Розкладання многочленів на множники 1. У шостому класі ми розкладали на множники числа. Наприклад, число 60 можна записати у вигляді добутку двох чисел 12 і 5: 60 = 12 × 5. Кажуть, що число 60 розкладено на два множники 12 і 5. Розкладати на множники можна і многочлени. Наприклад, аb + аc = а (b + c). Записавши многочлен аb + ac у вигляді добутку а (b + c), кажуть, що многочлен ab + аc розкладено на два множники а і b + c. Кожний із цих множників є многочленом (перший многочлен складається лише з одного члена). Розкласти многочлен на множники означає подати його як добуток Порівняйте
2. Розглянемо один зі способів розкладання многочленів на множники. Виконаємо множення одночлена на многочлен: x (x + y) = x × x + x × y = x 2+ xy. Перепишемо ці рівності у зворотному порядку: x 2+ xy = x × x + x × y = x (x + y). Многочлен x 2+ xy розклали на два множники x та x + y. Щоб розкласти многочлен x 2+ xy на множники, досить у його членах x 2та xy виділити спільний множник x: x 2+ xy = x × x + x × y, а потім на основі розподільної властивості множення записати одержаний вираз у вигляді добутку многочленів x та x + y. Описаний спосіб розкладання многочленів на множники називають способом винесення спільного множника за дужки.
Приклад 1. Розкласти на множники многочлен 12 х 3 y - 18 x 2 y 2. ● Спочатку знайдемо спільний числовий множник для коефіцієнтів 12 і -18. Якщо коефіцієнтами є цілі числа, то за 12 х 3 y - 18 x 2 y 2 =6 х 2 y × 2 х - 6 х 2 y × 3 y =6 х 2 y (2 х - 3 y). ● Приклад 2. Розкласти на множники многочлен -2 a 2 b - 8 a 2 b 2 + 10 ab 2. ● -2 a 2 b - 8 a 2 b 2 + 10 ab 2 =-2 ab (a + 4 аb - 5 b). ● Приклад 3. Розкласти на множники: 5 b (a - c) + 3(a - c). ● Даний вираз є сумою двох доданків, для яких спільним множником є вираз a - c. Винесемо цей множник за дужки: 5 b (a - c) + 3(a - c) = (a - c)(5 b + 3). ● Приклад 4. Розкласти на множники: 2 x (m - n) + y (n - m). ● Доданки мають множники m - n і n - m, які відрізняються тільки знаками. У виразі n - m винесемо за дужки -1, тоді другий доданок матиме вигляд - y (m - n) й обидва доданки матимуть спільний множник m - n. Отже, 2 x (m - n) + y (n - m) = 2 x (m - n) - y (m - n) = (m - n)(2 x - y). ● Приклад 5. Знайти значення виразу 8,5 а 2+ а 3, якщо а = 1,5. ● Розкладемо спочатку многочлен 8,5 а 2+ а 3 на множники: 8,5 а 2+ а 3= а 2(8,5 + а). Якщо а = 1,5, то: а 2(8,5 + а) = 1,52 × (8,5 + 1,5) = 2,25 × 10 = 22,5. ● Приклад 6. Розв’язати рівняння 4 х 2+ 5 х = 0. ● Розкладемо ліву частину рівняння на множники: х (4 х + 5) = 0. Добуток х (4 х + 5) дорівнює нулю лише тоді, коли хоча б один із множників дорівнює нулю: х = 0 або 4 х + 5 = 0, звідки х = 0 або х = -1,25. Відповідь. 0; -1,25. ● Усно 462. Знайдіть спільний множник членів многочлена: a) 8 + 4 b; б) 15 х - 10; в) 3 а + 3 ab; г) а 2 - 2 а; д) mn - n 2 + n; е) 18 a 4 b 3- 6 a 2 b 2. 463. Чи правильно розкладено на множники многочлен: а) 6 a + 6 = 6(a + 0); б) 6 a + 6 = 6(a + 6); в) 6 a + 6 = 6(a + 1); г) 4 xy - 2 y = y (4 х - 2); д) 4 xy - 2 y = - y (-4 х + 2); е) 4 xy - 2 y = 2 y (2 х - 1)?
Винесіть за дужки спільний множник: 464. а) 3 a + 3 b; б) 3 a + 6; в) 9 a - 18 b; г) -6 a + 6 b; д) 3 y 2 + 3 y - 6; е) -15 с - 10. 465. а) 5 a + 5; б) 5 a + 15 b; в) 15 x - 25 y; г) 2 x - 4 y + 8 z; д) -7 k + 7 m; е) -4 m - 2 n. Розкладіть на множники і зробіть перевірку: 466. а) 4 а + 12; б) 5 аb + 10 а; в) 4 аb - 2 b. 467. а) 2 b - 8 a; б) 6 xy + 24 x; в) 9 mn - 6 m. Розкладіть на множники: 468. а) ax + bx; б) ym - yn; в) - ca + cb; г) - xz - yz. 469. а) km + kn; б) - xa + ya; в) - bx - ax; г) ta - tb. 470. а) 9 ах - 9 bx; б) 3 ay - 6 y; в) -7 аb + 14 b; г) 10 x 2 - 15 х 3; д) 32 b 2- 24 b 4; е) -8 c 3 - 10 c 5. 471. а) 5 хy - 5 y; б) 8 ac - 6 ab; в) c 2 + c 5; г) 3 x 2+ 9 x; д) 15 y 2- 12 y 4; е) -24 n - 18 n 3. 472. a) а 3+ 3 а 2 - 10 a; б) 4 x 5 - 8 x 3 + 4 x 2; в) -9 a 5 - 27 a 3+ 18 a 4. 473. a) 2 x 4- x 3 - x 2; б) 2 c - 4 c 2 + 8 c 3; в) -5 b 4 + 10 b 2 + 5 b 5. Знайдіть значення многочлена: 474. а) х 3 - 1,5 x 2, якщо x = 2,5; б) xy + y 2, якщо x = -0,3; y = 10,3. 475. а) 2,4 a 2 - a 3, якщо a = 1,4; б) m 2 + mn, якщо m = 2,8; n = 7,2. Розв’яжіть рівняння: 476. а) х 2- 5 х = 0; б) 5 х 2+ 15 х = 0.
Рівень Б Розкладіть на множники: 478. а) a 2 b 3 + ab 4 - a 2 b 4; б) 36 x 4 y 3 - 48 x 6 y 4; в) 24 a 2 b 3 - 16 a 3 b 3- 40 a 3 b 2; г) -3 m 4 n 6 +1,2 m 5 n 5 - 4,2 m 5 n 6; д) 479. а) 2 x 4 z 3 + 4 x 4 z 4 - 4 x 4 z 5; б) 45 a 4 b 2 - 60 a 3 b 3+ 75 a 2 b 4; в) -3,6 m 2 n 5 + 5,4 m 3 n 4 - 9 m 2 n 4; г) 480. а) a (m + k) - b (m + k); б) 2 a (x - y) + 3(x - y); в) x (a - 2 b + 1) + y (a - 2 b + 1); г) m (a - b) + 3(b - a); д) a 2(n - 3) - 5(3 - n); е) (x - 2)2 + 4(x - 2); є) 2 x (a - b) - (a - b)2; ж) 4 x (a + b) + 2 х (a + b)2. 481. а) m (x - k) - n (x - k); б) c (a + b + 2) + 3(a + b + 2); в) a (s - t) + b (t - s); г) 2(a - b) - x (b - a); д) (m - 4)2 - 5(m - 4); е) x (m - n) + 2(m - n)2. Знайдіть значення многочлена: 482. а) б) 483. а) б) Розв’яжіть рівняння: 484. а) 4 y + 0,2 y 2= 0; б) 0,6 х 2- 0,24 х = 0; в) 485. а) 0,4 х - 2 х 2= 0; б) 1,5 х 2+ 0,3 х = 0; в) Доведіть, що значення виразу: 486. а) 198 - 197 ділиться на 18; б) 499 + 4910 ділиться на 50; в) 3 × 76 - 75 ділиться на 20; г) 310 + 2 × 312 + 311 ділиться на 22. 487. а) 119 + 118 ділиться на 12; б) 512 - 2 × 510 ділиться на 23.
488. Винесіть за дужки спільний множник: а) an + an + 2; б) 2 n + m + 2 n; в) 4 a 2 n - 4 an; г) a 2 n bn + anb 2 n ; д) хn + 2 хn + 2 + 3 хn + 3; е) х 2 m + 2 хm + хm + 2. 489. Доведіть, що значення виразу: а) 15 × 167 - 414 ділиться на 14; б) 3 × 215 + 212 - 214 ділиться на 21. 490. Доведіть, що коли: а) a + b = 4, то a 3 b 2 + a 2 b 3 - 4 a 2 b 2 = 0; б) a 2+ b 2 = 3 ab, то a 4 b 2 + a 3 b 3 + a 2 b 4 = 4 a 3 b 3; в) x + y + 2 = xy, то x 4 y 4 - x 3 y 4 - x 4 y 3 = 2 x 3 y 3. 491. Номер автобусного квитка складається з шести цифр. Квиток вважають «щасливим», якщо в його номері сума перших трьох цифр дорівнює сумі трьох останніх. Доведіть, що: а) якщо квиток з номером б) сума номерів «щасливих» квитків в) сума номерів усіх можливих «щасливих» квитків ділиться на 1001. Вправи для повторення 492. Периметр трикутника дорівнює 27 см. Знайдіть довжини сторін трикутника, якщо перша його сторона в 1,2 разу довша від другої, а друга ¾ на 5 см довша від третьої. 493. Автомобіль мав проїхати деякий шлях, рухаючись зі швидкістю 70 км/год. Якби він їхав зі швидкістю на 5 км/год більшою, то здолав би цей шлях на 20 хв швидше. Який шлях мав проїхати автомобіль? 494. Перемножте многочлени: а) (5 a – 7 b)(4 – b); б) (x 2 – y)(7 x – y 3); в) (y + 3)(y 2 – y + 4); г) (a 2 – 5 a + 3)(a – 7). 495. Візьміть у дужки два останні доданки, поставивши перед дужками знак «+»; знак «–»: a) 2+ с + d; б) а + b - 4 в) x - у - 3; г) 2 m - 3 n + k. 496. Обчисліть: а) 2,3 × 2,8 + 0,33 × 10,78 + 2,3 × 7,2 - 0,33 × 0,78; б) 7,7 × 1,6 - 0,03 × 500 + 1,8 × 1,6 + 1,6 × 0,5; в) 15. Розкладання многочленів на множники Вивчення цього способу розкладання многочленів на множники почнемо із прикладу на множення многочленів. Виконаємо множення двочлена a - b на двочлен x + y таким чином: (a - b)(x + y) = a (x + y) - b (x + y) = ax + ay - bx - by. Проводячи перетворення у зворотному порядку, многочлен ax + ay - bx - by можна розкласти на два множники a - b і x + y: ax + ay - bx - by = (ax + ау) + (- bx - by) = a (x + y) - b (x + y)= (x + y)(a - b). Проаналізуємо останні перетворення. Маємо многочлен, члени якого можна групувати так, щоб кожна група мала спільний множник (група ax + ay ¾ спільний множник а, його виносимо за дужки; група - bx - by ¾ спільний множник - b, його також виносимо за дужки). В утвореній різниці a (x + y) - b (x + y) маємо спільний множник x + y, виносимо його за дужки й Описаний спосіб розкладання многочленів на множники називають способом групування. Застосовуючи цей спосіб, треба утворювати групи членів, що мають спільний множник. Після винесення в кожній групі множників за дужки повинен утворитися спільний множник для всіх груп, який знову ж таки треба винести за дужки. Многочлен ax + аy - bx - by можна розкласти на множники, групуючи його члени по-іншому: ax + ay - bx - by = (ax - bx) + (ay - by)= x (a - b) + y (a - b) = (a - b)(x + y). Порівняйте
Приклад 1. Розкласти на множники многочлен 3 ах - 12 bх + 9 а - 4 bх 2. ● 3 ах - 12 bх + 9 а - 4 bх 2 = (3 ах + 9 а) - (4 bх 2 + 12 bх) = = 3 а (х + 3) - 4 bх (х + 3) = (х + 3)(3 а - 4 bх). ● Приклад 2. Розкласти на множники тричлен х 2 - 5 x + 6. ● Подамо другий член -5 x у вигляді -3 x - 2 x. Тоді: х 2 - 5 x + 6 = х 2 - 3 x - 2 x + 6 = х (x - 3) - 2(x - 3) = (х - 3)(x - 2). ● Усно 497. Вкажіть у кожному многочлені групи членів, які мають спільний множник, та назвіть цей множник: a) ax + аy + 5 x + 5 y; б) 2 a - 2 b + an - bn.
Розкладіть на множники: 498. a) ax + ay + 4 x + 4 y; б) 7 х + by + 7 y + bx; в) 6 m - 6 n + am - an; г) 6 m - 6 n - am + an; д) ma - na + mb - nb; е) 5 a - bх - 5 b + aх; є) a + 2 nb - b - 2 na; ж) 4 ay + 3 - 3 y - 4 a. 499. a) 2 a + 2 b + xa + xb; б) ma - mb + 3 a - 3 b; в) ka - kb - 5 a + 5 b; г) 6 c - ac - ab + 6 b ; д) x + y - bx - by; е) 7 am - 7 m + 5 ax - 5 х. 500. а) a 3 + a 2 + a + 1; б) x 3 – 4 x 2 + 2 x – 8; в) b 2 - ab - 2 b + 2 a; г) 10 x + xy + 10 y + x 2; д) 3 a - ax + 3 x - x 2; е) xya - xy + 5 a - 5. 501. а) x 3 + 2 x 2 + x + 2; б) a 6 + 5 a 4 + 5 a 2+ 25; в) a 2 + 2 ab + 3 a + 6 b; г) x 2 + 3 xa - 2 x - 6 a.
Розкладіть на множники: 502. а) a 2 + b 2 - a 3 y - ab 2 y; б) b 2 n + y 2 - bny - by; в) 3 а 2 c + 6 а 2 - 10 bc - 5 bc 2; г) 12 x 2 + 18 y + 10 x 3 + 15 xy; д) 0,9 ay + 1,2 y 2 - 1,2 ax - 1,6 xy; е) 503. а) x 2 y 2 + 2 y 3 - ax 2 - 2 ay; б) 2 a 2 b + 2 c - 4 abc - a; в) 6 x 3 y + 12 y 2 z 2 + 9 y 3 + 8 x 3 z 2; г) 0,2 mn 3 - 1,5 m 2 + 0,6 m 3 n - 0,5 n 2. 504. а) хa - хb + хc + 3 a - 3 b + 3 c; б) ax 2 - ay 2 + 4 az - 4 bx 2 + 4 by 2 -16 bz; в) -5 a - 5 b + 3 na + 3 nb - ma - mb; г) bn 2 + cn 2 - bp + bp 2 - cp + cp 2. 505. а) a 2 b + a + ab 2 + b + 2 ab + 2; б) сa - cb + c + ad - bd + d; в) 2 a 3 +2 a 2 b + 2 ab + 2 b 2 - a - b. Знайдіть значення виразу: 506. а) p 3 + pq 2 - p 2 q - q 3, якщо p = 1,5, q = 0,5; б) 2 a 3 - 6 ab + a 2 b - 3 b 2, якщо a = 8, b = 21; в) 4 x 3 + 4 x 2 y - 4 x 2 + 3 y 3 + 3 xy 2 - 3 y 2, якщо x = 507. а) 2 a 2 + ac - 2 ac 2 - c 3, якщо a = 17, c = 4; б) m 3 + m 2 n - 10 m + n 3 + n 2 m - 10 n, якщо m =
508. Розкладіть на множники: a 3 - a 2+ b 3 - b 2+ a 2 b + b 2 a. 509. Дано многочлен x 3 - х 2 + 3 x - 3. Доведіть, що для x > 1 він набуває лише додатних значень. 510. Для яких значень х значення многочленна 511. Розв’яжіть рівняння: (x 2- х)(6 + 5 x + x 2) = x 3(х + 4) - 5. 512. Розкладіть на множники тричлен: а) a 2 - 7 a + 10; б) x 2+ 5 x + 4; в) x 2 + 3 xy + 2 y 2; г) а 2 - 7 аb + 12 b 2. Розв’яжіть рівняння: 513. а) x 2- 3 x + 2 = 0; б) х 2 + 8 х + 15 = 0. 514. а) (x - 2)2 + 6(x - 2) + 8 = 0; б) (x 2 - 5 x)2 + 10(x 2 - 5 x) + 24 = 0. Вправи для повторення 515. Обчисліть: а) 33 × 93 - 273; б) 45 × 0,255 + 23 × 43 × 0,253; в) 25(26 - 1) - 23(28 - 22); г) 33(33 - 4) - 32(34 + 4). 516. За 3 товстих i 5 тонких зошитів Олег заплатив 5 грн. 60 коп. Товстий зошит дорожчий від тонкого на 80 коп. Скільки коштує товстий зошит? 517. На двох полицях було 95 книжок. Коли четверту частину книжок, що стояли на першій полиці, переставили на другу, то на другій полиці книжок стало на 5 більше, ніж на першій. Скільки книжок було на кожній полиці спочатку? 518. Площа першої ділянки дорівнює 63 га, а другої — 53 га. З першої ділянки господарство зібрало картоплі в 519. Прочитайте вираз словами: а) a + b; б) а - b; в) а 2 - b 2; г) (a – b)(а + b). Запитання і вправи для повторення § 4 1. Дайте означення многочлена. Наведіть приклади многочленів. 2. Який многочлен називають многочленом стандартного вигляду? 3. Що називають степенем многочлена? Наведіть приклад многочлена другого степеня. 4. Знайдіть суму та різницю многочленів 2 х + 4 і х + 2. 5. Як помножити одночлен на многочлен? 6. Як помножити многочлен на многочлен? 7. Що означає розкласти многочлен на множники? 8. Як розкладають многочлен на множники способом винесення
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 976; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.124.204 (0.014 с.) |

 Приклади розв’язання вправ
Приклади розв’язання вправ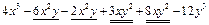 =
= Рівень А
Рівень А Рівень Б
Рівень Б ж)
ж) 
 е)
е) 
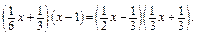

 Рівень В
Рівень В Рівень А
Рівень А 477. а) х 2+ 2 х = 0; б) 4 х - 2 х 2= 0.
477. а) х 2+ 2 х = 0; б) 4 х - 2 х 2= 0. х 3 y 4 z 2-
х 3 y 4 z 2-  х 2 y 3 z 3+
х 2 y 3 z 3+  х 3 y 3 z 4; е)
х 3 y 3 z 4; е)  abc 2 +
abc 2 +  ab 2 c -
ab 2 c - 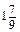 a 2 bc.
a 2 bc.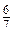 х 5 y 3 z 4-
х 5 y 3 z 4-  х 3 y 5 z 4+
х 3 y 5 z 4+  х 3 y 3 z 5.
х 3 y 3 z 5. xy 2 -
xy 2 - 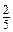 y 2, якщо x = 3; y = 0,5;
y 2, якщо x = 3; y = 0,5;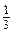 а 2 +
а 2 + 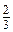 ab -
ab -  а, якщо а =
а, якщо а =  b =
b = 
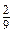 m 2 n +
m 2 n + 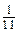 ху -
ху -  у 2 +
у 2 +  у, якщо х =
у, якщо х =  у =
у = 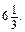
 х 2-
х 2- 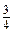 х -
х -  Рівень В
Рівень В є «щасливим», то й квиток з номером
є «щасливим», то й квиток з номером  — «щасливий»;
— «щасливий»;
 x 2 yz -
x 2 yz -  x +
x +  xy 2 z 2 -
xy 2 z 2 -  yz.
yz. y =
y = 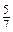 .
. n =
n = 
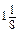 разу більше, ніж із другої. Яка врожайність картоплі на кожній ділянці, якщо врожайність на першій ділянці на 1,5 т менша, ніж на другій?
разу більше, ніж із другої. Яка врожайність картоплі на кожній ділянці, якщо врожайність на першій ділянці на 1,5 т менша, ніж на другій?


