
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Відомості з курсу математики 5–6 класівСодержание книги
Поиск на нашем сайте
Подільність натуральних чисел 1. Будь-яке натуральне число а, на яке ділиться дане натуральне число n, називають дільником числа n. 2. Будь-яке натуральне число n, яке ділиться на дане натуральне число a, називають кратним числу a.
3. Натуральне число називають простим, якщо воно має тільки два різних дільники: одиницю і це саме число. 4. Число, яке має більше ніж два дільники, називають складеним. 5. Кожне складене число можна записати у вигляді добутку кількох простих чисел, тобто розкласти його на прості множники. Наприклад: 120 = 23 · 3 · 5. 6. На 10 діляться ті й тільки ті натуральні числа, запис яких закінчується цифрою 0. 7. На 5 діляться ті й тільки ті натуральні числа, запис яких закінчується цифрами 0 або 5. 8. На 2 діляться ті й тільки ті натуральні числа, запис яких закінчується парною цифрою. 9. На 3 діляться ті й тільки ті натуральні числа, сума цифр яких ділиться на 3. 10. На 9 діляться ті й тільки ті натуральні числа, сума цифр яких ділиться на 9. Найбільший спільний дільник 11. Найбільше натуральне число, на яке ділиться кожне з даних чисел, називають найбільшим спільним дільником цих чисел. Для знаходження найбільшого спільного дільника двох чисел можна розкласти ці числа на прості множники і знайти добуток спільних множників. Наприклад: 144 = 2 · 2 · 2 · 2 · 3 · 3; 60 = 2 · 2 · 3 · 5; НСД(144; 66) = 2 · 2 · 3 = 12. Найменше спільне кратне 12. Найменшим спільним кратним натуральних чисел називають найменше натуральне число, яке ділиться на кожне з даних чисел. Щоб знайти найменше спільне кратне двох чисел, кожне з них можна розкласти на прості множники, до розкладу одного з чисел дописати з розкладу іншого числа ті множники, яких немає у розкладі першого, і перемножити записані числа. Наприклад: 144 = 2 · 2 · 2 · 2 · 3 · 3; 60 = 2 · 2 · 3 · 5; НСК(144; 60) = 2 · 2 · 2 · 2 · 3 · 3 · 5 = 720. Десяткові дроби 13. Додавання і віднімання десяткових дробів виконують порозрядно. Для цього дроби записують так, щоб відповідні розрядні одиниці й коми були одні під одними. Наприклад: 14. Щоб помножити один десятковий дріб на інший, потрібно виконати множення, не зважаючи на коми, а потім у добутку відокремити комою стільки десяткових знаків, скільки їх є в обох множниках разом.
Щоб поділити десятковий дріб на десятковий дріб, потрібно в діленому і дільнику перенести коми праворуч на стільки цифр, скільки десяткових знаків має дільник, а потім виконати ділення на натуральне число. Наприклад: Окремі випадки множення і ділення десяткових дробів:
Звичайні дроби 15. Основна властивість дробу. Якщо чисельник і знаменник звичайного дробу помножити або поділити на одне й те ж натуральне число, то отримаємо дріб, який дорівнює даному. Наприклад: 16. Щоб звести дроби до найменшого спільного знаменника, потрібно: 1) знайти найменше спільне кратне знаменників; 2) знайти додаткові множники, поділивши найменше спільне кратне на кожний знаменник; 3) чисельник і знаменник кожного дробу помножити на відповідний додатковий множник. Наприклад: зведемо до найменшого спільного знаменника дроби 1) НСК(4; 12; 16) = 48; 2) додаткові множники: 48: 4 = 12; 48: 12 = 4; 48: 16 = 3; 3) 17. Щоб додати дроби з однаковими знаменниками, потрібно до чисельника першого дробу додати чисельник другого й записати в чисельнику, а знаменник записати той самий. Щоб відняти дроби з однаковими знаменниками, потрібно від чисельника першого дробу відняти чисельник другого й записати в чисельнику, а знаменник записати той самий. Наприклад: Щоб додати або відняти дроби з різними знаменниками, потрібно їх спочатку звести до спільного знаменника. 18. Щоб перемножити два звичайні дроби, потрібно перемножити їх чисельники і добуток записати в чисельнику, перемножити їх знаменники і добуток записати в знаменнику. Щоб поділити один дріб на інший, досить ділене помножити на число, обернене дільнику. Наприклад: 19. Щоб звичайний дріб записати десятковим, досить чисельник дробу поділити на його знаменник. Наприклад: 20. Щоб знайти дріб від числа, потрібно число помножити на цей дріб. Наприклад: знайдемо 30% від 140 — це 0,3 від 140: 140 · 0,3 = 42. Щоб знайти число за даним значенням його дробу, потрібно це значення поділити на дріб. Наприклад: знайдемо число,
знайдемо число, 17% якого дорівнює 51: 17% = 0,17; 51: 0,17 = 300. 21. Щоб знайти відсоткове відношення двох чисел, потрібно знайти їх відношення і записати у відсотках.
Наприклад: знайдемо відсоткове відношення чисел 12 і 28:
Додатні та від’ємні числа 22. Модулем додатного числа і нуля є це ж число; модулем від’ємного числа є протилежне йому число:
Наприклад: |5,3| = 5,3; |0| = 0; |–1,8| = 1,8. 23. Щоб додати два від’ємних числа, потрібно додати їх модулі й поставити перед отриманим числом знак «–». Щоб додати два числа з різними знаками, потрібно знайти модулі чисел, від більшого модуля відняти менший модуль і поставити перед отриманим числом знак того доданка, модуль якого більший. Наприклад: –1,6 + (–2,3) = –3,9; –0,7 + 0,7 = 0; 3,2 + (–4,7) = –(4,7 – 3,2) = –1,5. 24. Щоб від одного числа відняти інше, досить до зменшуваного додати число, протилежне від’ємнику. Наприклад: –15 – (–9) = –15 + 9 = –6. 25. Щоб знайти добуток двох від’ємних чисел, досить перемножити модулі цих чисел. Щоб знайти добуток двох чисел з різними знаками, досить перемножити їх модулі і поставити перед одержаним числом знак «–». Наприклад: (–1,1) · (–0,9) = 1,1 · 0,9 = 0,99; 26. Щоб знайти частку двох від’ємних чисел, досить поділити модуль діленого на модуль дільника. Щоб знайти частку чисел з різними знаками, досить поділити модуль діленого на модуль дільника і поставити перед одержаним числом знак «–». Наприклад: –105: (–21) = 105: 21 = 5; 27. Щоб розкрити дужки, перед якими стоїть знак «+», потрібно опустити дужки і знак «+», що стоїть перед ними, і записати всі доданки, які були в дужках, зі своїми знаками: a + (– b + c) = a – b + c. Щоб розкрити дужки, перед якими стоїть знак «–», потрібно опустити дужки і знак «–», що стоїть перед ними, і записати всі доданки, які були в дужках, з протилежними знаками: a – (b – c) = a – (+ b – c) = a – b + c. 28. Щоб звести подібні доданки, потрібно додати їх коефіцієнти і результат помножити на спільну буквену частину. Наприклад: 7 a – 9 a + 4 a = (7 – 9 + 4) a = 2 a. ВІДПОВІДІ § 1 15. a = -3. 16. a = 23. 17. Вказівка. Обґрунтуйте, що для х = 2 значення лівої частини рівняння є непарним числом. 20. 375 грн. 21. 148 т. 32. а) 16; б) 1,125; в) Завдання для самоперевірки № 1 1-й рівень. 1. в). 2. б). 3. а); г). 4. б). 5. в). 2-й рівень. 2. а) Один; б) коренів немає; в) один; г) безліч. 3. а) 1; б)
§ 2 138. 2400 кг. 139. 160 деталей. 142. а) 22,45; б) 530. 143. а) Завдання для самоперевірки № 2 1-й рівень. 1. г). 2. б). 3. б). 4. в). 5. в). 2-й рівень. 1. 2 а – b. 2. 13 а + 8,2. § 3 249. 11; 1; 1; 5; 31. 250. -5; 0; 22. 254. а) 0; 100; 0; б) 0; 99; -1; в) 0; 1; 1; г) 0; 1; 1. 258. в) 2; г) -35. 259. 7 матчів виграла, 2 зіграла внічию. 260. -5; -10; -9. 278. а) 10 000; б) 1 000 000; в) 1; г) 100 000; д) Завдання для самоперевірки № 3 1-й рівень. 1. в). 2. б). 3. г). 4. в). 5. г). 2-й рівень. 1. а) х 8; б) х 5; в) х 15; г) х 24. 2. а) 44; б) 80; в) 1000. 3. а) 6 а 5; б) -1,5 а 5 b 5; в) 16 а 4 с 12. 4. а) 1; б) 20 000. 3-й рівень. 1. а) 636; б) 346; в) 224. 2. а) 36 х 8 у 8; б) 63 a 8 b 12 с 12; в) –0,0016 m 47 n 60; г) 6,25 a 11 х 11. 3. а) Наприклад, 2 a 2 b 2 × 4 a 10 b 10 × 8 b 6; б) (–4 a 5 b 8) × (–16 a 7 b 10); в) (4 a 4 b 6)3. 4. а) 256; б) 32. 4-й рівень. 1. а) 24 n + 10; б) 29 n + 22. 2. а) 1; б) 9. 3. 4. 4. а) 0; б) Коренів немає. § 4 346. а) 12; б) 2,21; в) -18. 347. а) 28; б) 0. 350. а) -0,44; б) -10. 351. а) 168; б) 2. 356. Вказівка. Припустимо, що коли x = n, де n — ціле число, то значення многочлена дорівнює нулю. Тоді правильною є рівність n 5 – 6 n 2 + 1 = 0. Обґрунтуйте, виходячи з цієї рівності, що 1 має ділитися на n, звідки n = 1 або n = –1. Однак, якщо n = 1 або n = –1, то дана рівність є неправильною. 359. а) -2; б) -0,6; в) 0,5; г) 0,75. 360. 18,4 км/год. 372. а) 0,8; б) -2. 373. а) 0,5; б) -0,8. 374. а) а 2 b 3; б) - х 4 - 2 х - 11; в) 2 xy - 2 х 2; г) -5 a 2 - 5 b - 3. 375. а) - х 2 - 5 х; б) 8 ab + 4 b 2; в) - n 2 + 7 n. 376. а) P = -3 х 2 - х + 3; б) Р = х 2 + 2; в) Р = 3 х 2. 377. -2 х 2 + 2 х + 6. 378. а) 2; б) -1,75. 379. а) -1,2; б) 2. 382. Порівну. 383. а = –1, b = 1. 387. 400 г. 391. б) -10 а 2 - 8 а; в) 2 а 5- а 3; г) -12 х 3 - 2 х. 392. а) -3 а 3; б) 4 b 3 - 4 b + 1. 393. а) 2 а 2; б) -2 у 2; в) -3 m - 6; г) 0. 394. а) с 3; б) -5 х 3 - 15 х 2; в) 4 а 2; г) 0. 395. а) -1; б) 2,5; в) -0,75; г) 6. 396. а) 1; б) 2,4. 397. а) -2 а 2 - 8 а + 8; б) 15 х 6 - 18 х 4; в) -8 m 4 n 3 + 8 m 4 n 2; г) -2 х 2 + x; д) 11 аbc; е) -18 х 5 у 2. 398. а) 2 а 3; б) -4 ху 2 + 2 х; в) -8 m 3 n 5; г)
Завдання для самоперевірки № 4 1-й рівень. 1. в). 2. в). 3. б). 4. г). 5. в). 6. б). 2-й рівень. 1. а) 2 а - 6; б) – х 2 - 3 х – 1. 2. а) 6 х 4 - 2 х 3 + 2 х 2; б) 6 а 2 - 19 ab + 10 b 2. 3. а) 4 х (1 – 3 х); б) -10(2 + a); § 5 551. а) 3; б) -5; в) -4 х 4; г) 64 с 8; д) 9 а 2 b 2; е) 8 а 2; є) -6 b 3 + 24 b. 552. а) 7; б) 25 - 2 с; в) а 6; г) -4 z 4; д) 0. 553. а) z 2 + 1; б)
599. 48; 60. 600. 12,6; 7. 601. 51 і 30 деталей. 616. а) (a + 1)(a + 3); б) (3 b - 3)(3 b + 1); в) (2 - 3 b)(6 + 3 b); г) (2 a - 5 - 5 b)(2 a - 5 + 5 b); д) (x + 1)(7 х + 5); е) (-2 a - 8 b)(4 a + 2 b). 617. а) (2 х - 4)(2 х + 2); б) (-2 а - 3)(6 а + 3); в) (- х + у)(9 х - 3 у). 618. -34,4; Завдання для самоперевірки № 5 1-й рівень. 1. г). 2. в). 3. в). 4. в). 5. г). 6. б). 2-й рівень. 1. –2 а + 10; 9. 2. а) 9 b 2 + 24 b + 16; б) 4 а 2 - 20 a + 25. 3. а) 2; б) -3. 4. а) (3 у - 4)(3 у + 4); |
||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.158.197 (0.011 с.) |

 ;
;  .
.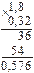 ;
;  = 3,6.
= 3,6.


 .
.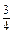 ,
,  і
і  :
: ;
;  ;
; 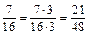 .
. ;
;  ;
;  .
. ;
; 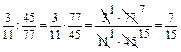 .
. .
. від 45:
від 45:  ;
; якого дорівнює 40:
якого дорівнює 40:
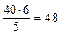 ;
; .
.



 г)
г)  33. а) 0,2; б)
33. а) 0,2; б)  34. а) –1; б)
34. а) –1; б)  35. а)
35. а)  б) 6. 36. а) –3; –2; –1; б) 0; 1; 2; 3;
б) 6. 36. а) –3; –2; –1; б) 0; 1; 2; 3;  39. а) 54 080 жителів; б) 50 000 жителів. 48. а) 2; б) -35; в) -10,2; г) 4. 49. а) 2; б) 0,7; в) -0,1; г) 6. 50. а) 5; б) 2,5; в) 2,5; г) 3,5; д) -4; е) коренів немає. 51. 0. 52. 4. 53. 3. 54. а) 1; б) 5; в) -2; г) коренем рівняння є будь-яке число. 55. а)
39. а) 54 080 жителів; б) 50 000 жителів. 48. а) 2; б) -35; в) -10,2; г) 4. 49. а) 2; б) 0,7; в) -0,1; г) 6. 50. а) 5; б) 2,5; в) 2,5; г) 3,5; д) -4; е) коренів немає. 51. 0. 52. 4. 53. 3. 54. а) 1; б) 5; в) -2; г) коренем рівняння є будь-яке число. 55. а)  б)
б)  в)
в)  г) 0. 56. а) 10; б) -1; в) -8; г)
г) 0. 56. а) 10; б) -1; в) -8; г)  57. г) –2; 9; д) 2,5; 5; е)
57. г) –2; 9; д) 2,5; 5; е)  . 58. а) –4; 4; б) –2; 2; в) коренів немає. 59. а) –4; 4; б) –5; 11; в) коренів немає; г) 7; д) –3; 3; е) –16; 16. 60. а) 1; б)
. 58. а) –4; 4; б) –2; 2; в) коренів немає. 59. а) –4; 4; б) –5; 11; в) коренів немає; г) 7; д) –3; 3; е) –16; 16. 60. а) 1; б)  61. а) 8; 12; б) -6; -2; в) -1; 1; г) -0,5; 1,5. 62. а) 5; б) –3; 2; в) 4; г) коренів немає; д) коренем рівняння є будь-яке недодатне число; е) коренем рівняння є будь-яке невід’ємне число. 63. а) 0; б) коренів немає; в) коренів немає. 64. 19. 69. 30 яблук. 70. 40 кг; 28 кг. 71. 18 і 15 комп’ютерів. 72. 784 га; 224 га. 73. 36 і 12 років. 74. 16 і 20 деталей. 75. 300 сторінок. 76. 90 км. 77. а) 9 см; 6 см; 10 см; б) 10,5 см; 5,5 см; 9 см. 78. Олег — 2 грн.; Сергій — 6 грн.; Віталій — 4 грн. 79. 130 кг; 150 кг; 180 кг. 80. 52,5 кг; 45 кг; 37,5 кг. 81. 20 км/год; 16 км/год; 12 км. 82. 66 і 54 яблук. 83. 400 км. 84. 200 км. 85. 30 км. 86. 21 км/год. 87. 40 км. 88. 56 км/год; 60 км/год. 89. 56, 14 і 11 років. 90. 60 і 35 книжок. 91. 80 семи-
61. а) 8; 12; б) -6; -2; в) -1; 1; г) -0,5; 1,5. 62. а) 5; б) –3; 2; в) 4; г) коренів немає; д) коренем рівняння є будь-яке недодатне число; е) коренем рівняння є будь-яке невід’ємне число. 63. а) 0; б) коренів немає; в) коренів немає. 64. 19. 69. 30 яблук. 70. 40 кг; 28 кг. 71. 18 і 15 комп’ютерів. 72. 784 га; 224 га. 73. 36 і 12 років. 74. 16 і 20 деталей. 75. 300 сторінок. 76. 90 км. 77. а) 9 см; 6 см; 10 см; б) 10,5 см; 5,5 см; 9 см. 78. Олег — 2 грн.; Сергій — 6 грн.; Віталій — 4 грн. 79. 130 кг; 150 кг; 180 кг. 80. 52,5 кг; 45 кг; 37,5 кг. 81. 20 км/год; 16 км/год; 12 км. 82. 66 і 54 яблук. 83. 400 км. 84. 200 км. 85. 30 км. 86. 21 км/год. 87. 40 км. 88. 56 км/год; 60 км/год. 89. 56, 14 і 11 років. 90. 60 і 35 книжок. 91. 80 семи- 4. 5 км/год. 3-й рівень. 1. Ні. 2. а)
4. 5 км/год. 3-й рівень. 1. Ні. 2. а)  б) 14. 3. 51 м; 30 м. 4. 5 год. 4-й рівень. 2. а)
б) 14. 3. 51 м; 30 м. 4. 5 год. 4-й рівень. 2. а)  б) –2; 2. 3. 300 м. 4. 1,5 кг.
б) –2; 2. 3. 300 м. 4. 1,5 кг.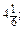 б) 4,6. 146. х = 2,5. 147. х = –7. 148. х = 2. 161. 120; 5040; 2 нулями; 24 нулями. 164. 23 числа. 166. а) 17,6 кг; б) 25 кг. 179. а) 44 а + 40; б) 8,5 b - 4 a; в) -6 у + 4; г) -2 х - 23 у - 6. 180. а) 2 х - 11 z; б) -14 а + 15 b - 3. 181. а) -6,9; б) -11; в) 28. 182. а) -4; б) 27. 192. а) 28 с + 26; б) х - 4,5; в) -6 х + 2 у + 3 z; г) 4 а -
б) 4,6. 146. х = 2,5. 147. х = –7. 148. х = 2. 161. 120; 5040; 2 нулями; 24 нулями. 164. 23 числа. 166. а) 17,6 кг; б) 25 кг. 179. а) 44 а + 40; б) 8,5 b - 4 a; в) -6 у + 4; г) -2 х - 23 у - 6. 180. а) 2 х - 11 z; б) -14 а + 15 b - 3. 181. а) -6,9; б) -11; в) 28. 182. а) -4; б) 27. 192. а) 28 с + 26; б) х - 4,5; в) -6 х + 2 у + 3 z; г) 4 а -  b; д) -6 х + 18; е) 15 n - 20. 193. а) 6 а + 12; б) 1,5 а - 5,4 b; в) 12 n + 18; г)
b; д) -6 х + 18; е) 15 n - 20. 193. а) 6 а + 12; б) 1,5 а - 5,4 b; в) 12 n + 18; г)  х -
х -  у +
у +  196. а) 1; б) 2. 197. а) –3; б) 0,5. 209. а) –5; 5; б) –7; –3; в) –3. 210. -15; 5; 20. 211. 60 км/год. 212.
196. а) 1; б) 2. 197. а) –3; б) 0,5. 209. а) –5; 5; б) –7; –3; в) –3. 210. -15; 5; 20. 211. 60 км/год. 212.  218. а) 35 - 54 а; б) 5 х - 10; в) х - 4 у - 9; г) 7 b + 5; д) -0,1 х + 2 у -1,2; е) 2,5 а + 15. 219. а) -47; б) 0,1. 220. 13. 221. х = 1,8.
218. а) 35 - 54 а; б) 5 х - 10; в) х - 4 у - 9; г) 7 b + 5; д) -0,1 х + 2 у -1,2; е) 2,5 а + 15. 219. а) -47; б) 0,1. 220. 13. 221. х = 1,8.
 е) 1; є) 1; ж)
е) 1; є) 1; ж)  279. а) 1000; б) 1 000 000; в) 1; д) 81; е)
279. а) 1000; б) 1 000 000; в) 1; д) 81; е)  282. а) аm + 2. 283. а) а 35; б) а 18; г) а 15. 284. б) а 15; г) а 12. 290. г) 33. 291. 20 виразів. 292. 117 км. 293. 250 м3. 306. а) -1,25 а 7 b 5; б) 0,27 а 6 b 5; в) - x 5 y 8; г) 16 а 6 b 12; д) -0,5 m 10 n 8; е) 1,1 а 7 b 7 с 7. 307. а) -25 m 4 n 3; б) -0,1 p 5 q 3; в) -9 а 12 b 5; г) -1,5 x 9 y 5 z 6. 312. а) 12; б) 4; в) 64; г) -24. 313. а) 400 000; б) 1; в) -32. 314. а) -10; б) 256. 315. а) 16 x 48; б) 2 x 22 n ; в) 8 а 4 n + 2 b 4 n + 2; г) - х 8 n + 5. 316. а) 1; б) 0,16. 317. У 8 разів. 318. а) 2; б) –1. 320. 1000 грн. 321. 855 км. 331. а) -2 а 5 b; б) a 3 b 3; в) - x 4 y 2; г) -112 a 7 b 4; д) -10 х 6 z 5; е) 81 a 12 b 16 с 20 d 4; є) -0,2 a 5 b 5; ж) -10 х 3 у 5; з) -256 m 8 n 21. 333. а) 27; б) -320. 334. в) 1; г) 256. 337. а) 0; б) коренів немає; в) 0.
282. а) аm + 2. 283. а) а 35; б) а 18; г) а 15. 284. б) а 15; г) а 12. 290. г) 33. 291. 20 виразів. 292. 117 км. 293. 250 м3. 306. а) -1,25 а 7 b 5; б) 0,27 а 6 b 5; в) - x 5 y 8; г) 16 а 6 b 12; д) -0,5 m 10 n 8; е) 1,1 а 7 b 7 с 7. 307. а) -25 m 4 n 3; б) -0,1 p 5 q 3; в) -9 а 12 b 5; г) -1,5 x 9 y 5 z 6. 312. а) 12; б) 4; в) 64; г) -24. 313. а) 400 000; б) 1; в) -32. 314. а) -10; б) 256. 315. а) 16 x 48; б) 2 x 22 n ; в) 8 а 4 n + 2 b 4 n + 2; г) - х 8 n + 5. 316. а) 1; б) 0,16. 317. У 8 разів. 318. а) 2; б) –1. 320. 1000 грн. 321. 855 км. 331. а) -2 а 5 b; б) a 3 b 3; в) - x 4 y 2; г) -112 a 7 b 4; д) -10 х 6 z 5; е) 81 a 12 b 16 с 20 d 4; є) -0,2 a 5 b 5; ж) -10 х 3 у 5; з) -256 m 8 n 21. 333. а) 27; б) -320. 334. в) 1; г) 256. 337. а) 0; б) коренів немає; в) 0. а 2 b 2 - 4 а 4. 405. а) 5; б) 0,7; в) 3; г) 2. 406. а) -15; б) 2; в) 1; г) 1,5. 407. а) -1; б) 4. 408. а) 0; б) 3. 409. 1,5; 8,5. 410. 60 см2. 411. 200 м2. 412. а) 0; б) - аn; в) х 3 n + 4 + х 3 n + 2. 415. Хлопців на 5 більше, ніж дівчат. 416.
а 2 b 2 - 4 а 4. 405. а) 5; б) 0,7; в) 3; г) 2. 406. а) -15; б) 2; в) 1; г) 1,5. 407. а) -1; б) 4. 408. а) 0; б) 3. 409. 1,5; 8,5. 410. 60 см2. 411. 200 м2. 412. а) 0; б) - аn; в) х 3 n + 4 + х 3 n + 2. 415. Хлопців на 5 більше, ніж дівчат. 416.  л. Вказівка. Після першого відливання і доливання води в 1 л суміші міститься
л. Вказівка. Після першого відливання і доливання води в 1 л суміші міститься 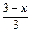 л спирту. 417. 90 км. 418. 180 км. 419. 60 піратів. 427. а) 6 а 2 - 4; б) -12; в) -15; г) а 3 + а; д) а 2 - 3 b 2; е) -4 y 2. 428. а) 7 х + 6; б) 3 а 2; в) 5 ab - 8 b 2; г) 2 m 2 -15 n 2. 429. а) 5; б) 0,6. 430. а) 4; б) 1. 435. а) 12 а 2 - 10; б) 45 х – 4; в) 5 а; г) 7 b 3; д) 14 х 4 у 2. 436. а) 18 х 2 - 15; б) -35 b + 10; в) х 3 + 9 у 3; г) 2 ab. 437. а) 1,8; б) 2; в) -1; г) 2. 438. а)
л спирту. 417. 90 км. 418. 180 км. 419. 60 піратів. 427. а) 6 а 2 - 4; б) -12; в) -15; г) а 3 + а; д) а 2 - 3 b 2; е) -4 y 2. 428. а) 7 х + 6; б) 3 а 2; в) 5 ab - 8 b 2; г) 2 m 2 -15 n 2. 429. а) 5; б) 0,6. 430. а) 4; б) 1. 435. а) 12 а 2 - 10; б) 45 х – 4; в) 5 а; г) 7 b 3; д) 14 х 4 у 2. 436. а) 18 х 2 - 15; б) -35 b + 10; в) х 3 + 9 у 3; г) 2 ab. 437. а) 1,8; б) 2; в) -1; г) 2. 438. а)  x 2 y 3 z 2(xy - 2 z + 7 xz 2); е)
x 2 y 3 z 2(xy - 2 z + 7 xz 2); е) 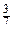 x 3 y 3 z 4(2 x 2 - y 2+ 4 z). 480. а) (m + k)(a - b); г) (a - b)(m - 3); е) (x - 2)(x + 2); є) (a - b)(2 х - a + b); ж) 2 х (a + b)(2 + a + b). 481. а) (x - k)(m - n); в) (s - t)(a - b); г) (a - b)(2 + x); д) (m - 4)(m - 9); е) (m - n)(х + 2 m - 2 n). 482. а) 0,5; б)
x 3 y 3 z 4(2 x 2 - y 2+ 4 z). 480. а) (m + k)(a - b); г) (a - b)(m - 3); е) (x - 2)(x + 2); є) (a - b)(2 х - a + b); ж) 2 х (a + b)(2 + a + b). 481. а) (x - k)(m - n); в) (s - t)(a - b); г) (a - b)(2 + x); д) (m - 4)(m - 9); е) (m - n)(х + 2 m - 2 n). 482. а) 0,5; б)  483. а) 5; б) 0. 484. а) 0; -20; б) 0; 0,4; в) 0;
483. а) 5; б) 0. 484. а) 0; -20; б) 0; 0,4; в) 0;  . 485. а) 0; 0,2; б) 0; -0,2; в) 0;
. 485. а) 0; 0,2; б) 0; -0,2; в) 0;  492. 12 см; 10 см; 5 см. 493. 350 км. 496. а) 26,3; б) 1; в)
492. 12 см; 10 см; 5 см. 493. 350 км. 496. а) 26,3; б) 1; в) 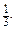 498. є) (1- 2 n)(a - b); ж) (у - 1)(4 а - 3). 499. г) (с + b)(6 - a); д) (х + у)(1- b); е) (a - 1)(7 m + 5 x). 500. а) (a + 1)(a 2 + 1); б) (x – 4)(x 2+ 2); в) (b - a)(b - 2); г) (х + у)(10 + х); д) (3 - х)(а + х); е) (а - 1)(ху + 5). 501. а) (х + 2)(х 2 + 1); б) (а 2 + 5)(а 4+ 5); в) (а + 2 b)(a + 3); г) (х + 3 a)(х - 2). 502. а) (a 2+ b 2)(1 - ay); б) (b - y)(bn - y); в) (c + 2)(3 a 2- 5 bc); г) (2 x 2 + 3 у)(6 + 5 х); д) (3 y - 4 х)(0,3 а + 0,4 y); е)
498. є) (1- 2 n)(a - b); ж) (у - 1)(4 а - 3). 499. г) (с + b)(6 - a); д) (х + у)(1- b); е) (a - 1)(7 m + 5 x). 500. а) (a + 1)(a 2 + 1); б) (x – 4)(x 2+ 2); в) (b - a)(b - 2); г) (х + у)(10 + х); д) (3 - х)(а + х); е) (а - 1)(ху + 5). 501. а) (х + 2)(х 2 + 1); б) (а 2 + 5)(а 4+ 5); в) (а + 2 b)(a + 3); г) (х + 3 a)(х - 2). 502. а) (a 2+ b 2)(1 - ay); б) (b - y)(bn - y); в) (c + 2)(3 a 2- 5 bc); г) (2 x 2 + 3 у)(6 + 5 х); д) (3 y - 4 х)(0,3 а + 0,4 y); е)  503. а) (y 2- a)(x 2 + 2 y); б) (a - 2 c)(2 ab - 1); в) (2 x 3+ 3 y 2)(3 y + 4 z 2); г) (n 2+ 3 m 2)(0,2 mn - 0,5). 504. а) (a - b + c)(x + 3); б) (x 2 - y 2 + 4 z)(a - 4 b); в) (a + b)(-5 + 3 n - m); г) (b + c)(n 2 + p 2 - p). 505. а) (a + b + 2)(ab + 1); б) (a - b + 1)(с + d); в) (a + b)(2 a 2 + 2 b - 1). 506. а) 2,5; б) 37; в) 0. 507. а) 38; б)
503. а) (y 2- a)(x 2 + 2 y); б) (a - 2 c)(2 ab - 1); в) (2 x 3+ 3 y 2)(3 y + 4 z 2); г) (n 2+ 3 m 2)(0,2 mn - 0,5). 504. а) (a - b + c)(x + 3); б) (x 2 - y 2 + 4 z)(a - 4 b); в) (a + b)(-5 + 3 n - m); г) (b + c)(n 2 + p 2 - p). 505. а) (a + b + 2)(ab + 1); б) (a - b + 1)(с + d); в) (a + b)(2 a 2 + 2 b - 1). 506. а) 2,5; б) 37; в) 0. 507. а) 38; б)  508. (а + b - 1)(a 2 + b 2). 510. Якщо х > 3, то значення многочлена додатні; якщо х < 3, ¾ від’ємні. 511. 1; 5. 512. а) (а - 2)(а - 5); б) (х + 1)(х + 4); в) (x + y)(x + 2 y); г) (a - 3 b)(a - 4 b). 513. а) 1; 2; б) -5; -3. 514. а) -2; 0; б) 1; 2; 3; 4. 516. 1 грн. 20 коп. 517. 60 і 35 книжок. 518. 26,5 т; 28 т. 525. а) 12 b 2 - 14 b; б) 4 x + 8; в) - ab 2 + 2 a - 1; г) 0; д) 4 bc; е) 0. 527. а) -1; б) -1,5; в) 16; г) -31. 530. 7 см; 5 см. 531. а) 0,6; б) коренів немає; в) -1. 533. а) (а + b)(2 + х); б) (х - y)(3 - а); в) (х + 2)(х 2+ 1); г) (1 - 2 y)(0,1 x + 0,2 y); д) 5(b + 2)(a 2- 2 bc); е) (4 z - 5 y)(x 2- 5 y 2). 534. а) (x - 7)(х - 2); б) (х + 2)(x + 6). 535. а) 0; 3; б) 0; -2; в) 0; -2,5; г) 0;
508. (а + b - 1)(a 2 + b 2). 510. Якщо х > 3, то значення многочлена додатні; якщо х < 3, ¾ від’ємні. 511. 1; 5. 512. а) (а - 2)(а - 5); б) (х + 1)(х + 4); в) (x + y)(x + 2 y); г) (a - 3 b)(a - 4 b). 513. а) 1; 2; б) -5; -3. 514. а) -2; 0; б) 1; 2; 3; 4. 516. 1 грн. 20 коп. 517. 60 і 35 книжок. 518. 26,5 т; 28 т. 525. а) 12 b 2 - 14 b; б) 4 x + 8; в) - ab 2 + 2 a - 1; г) 0; д) 4 bc; е) 0. 527. а) -1; б) -1,5; в) 16; г) -31. 530. 7 см; 5 см. 531. а) 0,6; б) коренів немає; в) -1. 533. а) (а + b)(2 + х); б) (х - y)(3 - а); в) (х + 2)(х 2+ 1); г) (1 - 2 y)(0,1 x + 0,2 y); д) 5(b + 2)(a 2- 2 bc); е) (4 z - 5 y)(x 2- 5 y 2). 534. а) (x - 7)(х - 2); б) (х + 2)(x + 6). 535. а) 0; 3; б) 0; -2; в) 0; -2,5; г) 0; 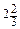 . 536. а) 2; 3; б) -3; -1. 537. а) -18; б) 85; в) 42. 541. 0,5.
. 536. а) 2; 3; б) -3; -1. 537. а) -18; б) 85; в) 42. 541. 0,5. б) x 3 + 6 x 2 y + 11 xy 2 + 6 y 3. 2. –9. 3. а) –6; б)
б) x 3 + 6 x 2 y + 11 xy 2 + 6 y 3. 2. –9. 3. а) –6; б) 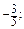
 4. а)
4. а)  б) (х + 2)(х + а). 5. 20 см2; 14 см2.
б) (х + 2)(х + а). 5. 20 см2; 14 см2. в) - х 2 -
в) - х 2 -  г)
г)  554. а)
554. а)  б) 6 b 2-
б) 6 b 2- 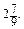 555. а) b 4 - 1; б) 16 х 4 - 1; в) 16 - у 4; г) 81 n 4 - 256; д) у 4 - 16 z 4; е) а 8 - 1. 556. а) 81 - с 4; б) z 4 - 625; в) 256 x 4 - у 4; г) 81 k 8 - 16. 559. а) 5; б) 0,5; в) 1; г) 0. 560. а) 0,5; б) 0,4. 561. а) 0; б) a 32 - b 32. 562. Вказівка. Врахувавши, що a - b = 1, ліву частину рівності можна записати у вигляді (a - b)(a + b)(a 2 + b 2)(a 4 + b 4)(a 8 + b 8). 564. -1. 566. 5 км/год. 567. 10%. 568. 1,35 кг. 576. а) 2 а 2 + 2; б) b 2; в) -20 x; г) 2 x - 2. 577. а) 16; б) 2 х 2 + 8. 578. а) 1; б) -2. 579. а) -5; б) 1. 588. а) -8 a; б) 1; в) 12 n 2 + 2; г) a 2 + b 2 + 2 ab. 589. а) 2 a 2 + 8 b 2; б) х 4 + 25 x; в) a 2 + b 2 - 1. 590. а) -0,3; б) 2; в) 0,5; г) 0,25. 591. а) 1; б) -9; в) -1. 593. -4 а 20 b 20. 596. 2. 597. Вказівка. Розгляньте можливі випадки: 1) m = 5 k + 1; 2) m = 5 k + 2; 3) m = 5 k + 3; 4) m = 5 k + 4, де k ¾ ціле число.
555. а) b 4 - 1; б) 16 х 4 - 1; в) 16 - у 4; г) 81 n 4 - 256; д) у 4 - 16 z 4; е) а 8 - 1. 556. а) 81 - с 4; б) z 4 - 625; в) 256 x 4 - у 4; г) 81 k 8 - 16. 559. а) 5; б) 0,5; в) 1; г) 0. 560. а) 0,5; б) 0,4. 561. а) 0; б) a 32 - b 32. 562. Вказівка. Врахувавши, що a - b = 1, ліву частину рівності можна записати у вигляді (a - b)(a + b)(a 2 + b 2)(a 4 + b 4)(a 8 + b 8). 564. -1. 566. 5 км/год. 567. 10%. 568. 1,35 кг. 576. а) 2 а 2 + 2; б) b 2; в) -20 x; г) 2 x - 2. 577. а) 16; б) 2 х 2 + 8. 578. а) 1; б) -2. 579. а) -5; б) 1. 588. а) -8 a; б) 1; в) 12 n 2 + 2; г) a 2 + b 2 + 2 ab. 589. а) 2 a 2 + 8 b 2; б) х 4 + 25 x; в) a 2 + b 2 - 1. 590. а) -0,3; б) 2; в) 0,5; г) 0,25. 591. а) 1; б) -9; в) -1. 593. -4 а 20 b 20. 596. 2. 597. Вказівка. Розгляньте можливі випадки: 1) m = 5 k + 1; 2) m = 5 k + 2; 3) m = 5 k + 3; 4) m = 5 k + 4, де k ¾ ціле число. 619. 44;
619. 44;  620. а) -2; -4; б) 1; -0,2; в) -5; -1; г) -6; 0. 621. а) 2; 3; б) 1; 3.
620. а) -2; -4; б) 1; -0,2; в) -5; -1; г) -6; 0. 621. а) 2; 3; б) 1; 3. 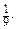 643. а) 4; б) -6. 644. а) 3; б) -5. 645. а) 25; б)
643. а) 4; б) -6. 644. а) 3; б) -5. 645. а) 25; б)  647. х =
647. х =  у = -2. 648. Коренем є будь-яке число. 649. а) 0,0081; б) 25. 650. 0; 0,25. 664. в) (3 а 2 - 5)(9 а 4 + 15 а 2 + 25); е) (10 - аb 3 c 4)(100 + 10 аb 3 c 4 + а 2 b 6 c 8). 665. в) (0,4 x 3 y 2 z - 3)(0,16 x 6 y 4 z 2 + 1,2 x 3 y 2 z + 9). 668. а) а 3; б) x 6; в) 0; г) 16. 669. а) x 3; б) 2 b 3. 670. а) -2; б) 4,5. 671. а) 1; б) 8. 675. 11,375. 676. а) 2 х 2 + 2 у 2; б) 10 ab; в) - a 2. 677. а) 9; б) 12. 678. 105 км. 679. а) 7; -0,6; б) 0; 1; -3. Вказівка. | а | = | b |, якщо a = b або a = - b. 680. г) 4 а (a - 1)(a + 1); д) х 2(х - 1)(х + 1); е) с (а - 3 b)(а + 3 b); ж) с (3 + b)(9 - 3 b + b 2). 681. г) 3 y 2(y - 1)(y + 1); д) 2 х (3 y - 1)(3 y + 1); є) 6 а (1 - b)(1 + b + b 2); ж) а 3(1 - а)(1 + а). 682. б) -(b - с)2; д) а (3 а + 1)2; е) m (1 - 5 m)2. 683. в) -6(а – 2 b)2; г) х (х - 6)2. 684. а) 800; б) 125. 685. а) 300; б) 26 000. 686. а) -3; 3; б) -0,5; 0,5. 687. а) -5; 5; б) -0,2; 0,2.
у = -2. 648. Коренем є будь-яке число. 649. а) 0,0081; б) 25. 650. 0; 0,25. 664. в) (3 а 2 - 5)(9 а 4 + 15 а 2 + 25); е) (10 - аb 3 c 4)(100 + 10 аb 3 c 4 + а 2 b 6 c 8). 665. в) (0,4 x 3 y 2 z - 3)(0,16 x 6 y 4 z 2 + 1,2 x 3 y 2 z + 9). 668. а) а 3; б) x 6; в) 0; г) 16. 669. а) x 3; б) 2 b 3. 670. а) -2; б) 4,5. 671. а) 1; б) 8. 675. 11,375. 676. а) 2 х 2 + 2 у 2; б) 10 ab; в) - a 2. 677. а) 9; б) 12. 678. 105 км. 679. а) 7; -0,6; б) 0; 1; -3. Вказівка. | а | = | b |, якщо a = b або a = - b. 680. г) 4 а (a - 1)(a + 1); д) х 2(х - 1)(х + 1); е) с (а - 3 b)(а + 3 b); ж) с (3 + b)(9 - 3 b + b 2). 681. г) 3 y 2(y - 1)(y + 1); д) 2 х (3 y - 1)(3 y + 1); є) 6 а (1 - b)(1 + b + b 2); ж) а 3(1 - а)(1 + а). 682. б) -(b - с)2; д) а (3 а + 1)2; е) m (1 - 5 m)2. 683. в) -6(а – 2 b)2; г) х (х - 6)2. 684. а) 800; б) 125. 685. а) 300; б) 26 000. 686. а) -3; 3; б) -0,5; 0,5. 687. а) -5; 5; б) -0,2; 0,2.  в) (c - 3 - k)(c - 3 + k); г) (2 x - y - 2)(2 x + y + 2). 693. а) (m + n - k)(m + n + k); б)
в) (c - 3 - k)(c - 3 + k); г) (2 x - y - 2)(2 x + y + 2). 693. а) (m + n - k)(m + n + k); б)  в) (a - 4 - b)(a - 4 + b); г) (p - q + 5)(p + q - 5). 695. 0. 696. а) (a + b)(a - b + 1); б) (x - a)(x + a + 1);
в) (a - 4 - b)(a - 4 + b); г) (p - q + 5)(p + q - 5). 695. 0. 696. а) (a + b)(a - b + 1); б) (x - a)(x + a + 1);  г)
г)  752. в) х 2 у 2(х - у)(х + у);
752. в) х 2 у 2(х - у)(х + у); 


