Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вирази зі змінними. Цілі виразиСодержание книги
Поиск на нашем сайте
1. Вирази зі змінними. Розглянемо кілька задач. Задача 1.Довжина прямокутної ділянки дорівнює 42 м, а ширина — на b м менша від довжини. Записати у вигляді виразу площу ділянки. ● Ширина ділянки дорівнює (42 - b) м, а площа — 42(42 - b) м2. Відповідь. 42(42 - b) м2. ● Вираз 42(42 - b) містить букву b і такий вираз ми називали буквеним виразом. Букві b можна надавати різні значення, b може дорівнювати 0,8; 5; 7,2; 10 тощо, тобто значення b можна змінювати, а тому b називають змінною, а вираз 42(42 – b) — виразом зі змінною. Задача 2.Довжина прямокутної ділянки дорівнює а м, а ширина — на b м менша від довжини. Записати у вигляді виразу площу ділянки. ● Ширина ділянки дорівнює (а - b) м, а площа — а (а - b) м2. Відповідь. а (а - b) м2. ● Букви a і b також можуть набувати різних значень, тому a і b — змінні, а вираз a (a – b) — вираз із двома змінними. Вираз зі змінними утворюють зі змінних, чисел, знаків дій і дужок. Виразом зі змінною вважають й окремо взяту змінну. Якщо у вираз 42(42 - b) замість змінної підставити певне число, наприклад, число 12, то одержимо числовий вираз 42 × (42 - 12), значення якого дорівнює: 42 × (42 - 12) = 42 × 30 = 1260. Одержане число 1260 називають значенням виразу 42(42 - b) для значення змінної b = 12. Значення виразу а (а - b) для а = 30, b = 7 дорівнює: 30 × (30 - 7) = 30 × 23 = 690. Розглянемо вираз зі змінною: 2. Цілі вирази. Порівняємо вирази а + b, 7 а, з виразами
Вирази першої групи не містять дії ділення на вираз зі змінними. Такі вирази називають цілими. Вирази другої групи містять дію ділення на вираз зі змінними. Такі вирази називають дробовими. Ми вивчатимемо їх у 8 класі. У 7 класі розглядатимемо тільки цілі вирази. 3. Формули. Вирази зі змінними використовують для запису формул. Наприклад: S = ab ¾ формула для обчислення площі прямокутника; V = abc ¾ формула для обчислення об’єму прямокутного паралелепіпеда. Формулою n = 2 k (де k ¾ ціле число) задаються парні числа, а формулою n = 2 k + 1 ¾ непарні числа.
Формулами можна задати всі цілі числа, які при діленні на задане натуральне число дають одну й ту ж остачу.
Розглянемо спочатку приклад ділення двох натуральних чисел. Поділимо 48 на 5 з остачею:
Одержали: 9 ¾ неповна частка, 3 ¾ остача. Натуральні числа, не кратні числу 5, при діленні на 5 можуть дати в остачі 1, 2, 3 або 4. Числа, кратні числу 5, діляться (націло) на 5. Ще кажуть, що такі числа при діленні на 5 дають в остачі 0. Поділивши 48 на 5, ми знайшли два числа 9 та 3 (неповну частку та остачу), використовуючи які, число 48 можна записати у вигляді 48 = 5 × 9 + 3. Ділення будь-якого цілого числа на натуральне з остачею зводиться до знаходження подібної рівності. Поділити ціле число m на натуральне число n з остачею означає знайти такі цілі числа k і r, щоб виконувалась рівність m = nk + r, де 0 £ r £ n – 1. За цих умов число k називають неповною часткою, а r ¾ остачею від ділення m на n. Остач від ділення цілих чисел на натуральне число п може бути п: 0, 1, 2,..., п - 2, п - 1. Знайдемо для прикладу остачу від ділення числа –17 на число 3. Для цього запишемо число –17 у вигляді –17 = 3 k + r, де k і r — цілі числа, до того ж, 0 £ r £ 2. Щоб число r лежало в межах від 0 до 2, потрібно узяти k = –6. Тоді легко знайти, що r = 1. Маємо правильну рівність -17 = 3 × (-6) + 1. Отже, число –17 при діленні на 3 дає в остачі 1. Цілі числа при діленні на 3 можуть давати в остачі 0, 1 або 2. Відповідно до цього їх можна поділити на 3 групи.
Отже, формулами m = 3 k, m = 3 k + 1 і m = 3 k + 2, де k ¾ довільне ціле число, задаються усі цілі числа, які при діленні на 3 дають в остачі відповідно 0, 1, 2. Про числа m = 3 k ще кажуть, що вони діляться (націло) на 3. Так, –9 ділиться на 3.
Приклад 1. Записати у вигляді виразу: а) добуток числа а і суми чисел b та с; б) частку різниці чисел m та n і числа 7; в) різницю числа а і добутку чисел m та n. ● а) а (b + с); б) (m - n): 7; в) а - mn. ● Зауваження. Читаючи словами числові вирази чи вирази зі змінними, першою називають останню по порядку виконання дію, далі передостанню і т. д. Приклад 2. Знайти значення виразу а 2(b + c), якщо а = 4, b = -7, с = 2. ● Якщо а = 4, b = -7, с = 2, то а 2(b + c) = 42 × (-7 + 2) = 16 × (-5) = -80.
Відповідь. -80. ● Приклад 3. Знайти значення виразу (m + n)2 - 3 n, якщо m = ● Якщо m = (m + n)2 - 3 n = Відповідь. Приклад 4.Записатиу вигляді виразу число, яке має 9 сотень, c десятків, d одиниць. ● 9 · 100 + с · 10 + d = 900 + 10 с + d. ● Усно 123. Серед записів вкажіть числові вирази, вирази зі змінними та записи, що не є виразами: а) 7,2: 3; б) 5; в) 2 х = 3; г) (18 - 3): 5 = 3; д) a - c; е) 15 – 8 а; є) 124. Прочитайте словами вирази зі змінними: а) 5 + х; б) y: 7; в) 2 ab; г) (abc - 2): 4; д) (a - 3): а; е) Які з даних виразів є цілими виразами? 125. Складіть три вирази із числа 7 та змінних a і b. 126. Складіть два вирази із чисел 5 і 11 та змінної х.
Запишіть у вигляді виразу: 127. а) суму чисел 12 і а; б) частку чисел - с і 7; в) куб числа а; г) піврізницю чисел а і b. 128. а) добуток числа 3 і суми чисел а та с; б) потроєний добуток чисел b і с; в) різницю числа а і квадрата числа с. 129. а) різницю чисел b і 9; б) добуток чисел 3 і - а; в) квадрат числа х; г) півсуму чисел m і n; д) добуток різниці чисел 3 та с і числа 5; е) подвоєну частку чисел а і с. Знайдіть значення виразу: 130. а) 7 b - 3, якщо b = -9; б) 0,11 - 4 c 2, якщо c = 0,2; в) 3 а + b, якщо а = -3; b = 8; г) аb - 4 c, якщо а = -0,4; b = 7; c = 0,12. 131. а) 132. а) -2 а + 5,2, якщо а = -3; б) (1 - 4 s)2, якщо s = 2; в) 12(3 у - 5), якщо y = 1,5; г) x - 2 y, якщо х = 11; y = -5,5; д) 3(а + b) - 2 c, якщо а = 3,2; b = -7,7; c = 2,5. Заповніть таблицю: 133.
134.
135.
136.
137. Швидкість автомобіля дорівнює 75 км/год. Запишіть у вигляді виразу шлях, який автомобіль проїде за t год. 138. На склад завезли n мішків борошна по 50 кг у кожному. Запишіть у вигляді виразу масу всього завезеного борошна. Знайдіть значення цього виразу, якщо n = 48. 139. Робітник за день виготовляє 32 деталі. Запишіть у вигляді виразу кількість деталей, які робітник виготовить за k днів. Знайдіть значення цього виразу, якщо k = 5. 140. З ділянки, площа якої дорівнює а га, господарство зібрало по 38 ц пшениці з гектара, а з ділянки, площа якої дорівнює b га, ¾ по 42 ц. Запишіть у вигляді виразу масу пшениці, зібраної господарством з обох ділянок. 141. Майстерня закупила 50 м тканини по а грн. за метр і 30 м тканини по b грн. за метр. Запишіть у вигляді виразу вартість усієї тканини.
Знайдіть значення виразу: 142. а) б) 143. а) б) 144. За формулою S = v t знайдіть шлях (у кілометрах), якщо: а) v = 75 км/год; t = 0,6 год; б) v = 75 км/год; t = 20 хв; в) v = 20 м/с; t = 2 год; г) v = 900 м/хв; t = 25 с. 145.За формулою S = v t знайдіть шлях (у метрах), якщо: а) v = 8 м/с; t = 5 хв; б) v = 15 км/год; t = 6 хв. 146. Для яких значень х значення виразу 2 х + 5 дорівнює 10? 147. Для яких значень х значення виразу 4 – 2 х дорівнює 18? 148. Для яких значень х значення виразів 3 х - 12 і -4 - х дорівнюють одне одному? 149. Відомо, що для деяких значень х та y значення виразу хy дорівнює 0,4. Якого значення для тих самих значень х та y набуває вираз: а) 10 хy; б) 0,1 хy; в) 150. Запишіть формулу цілих чисел, які при діленні на 4 дають в остачі 1. 151.Запишіть формулу цілих чисел, які при діленні на 5 дають в остачі 2. Запишіть у вигляді виразу число, яке має: 152. а) а десятків і b одиниць; б) а сотень і с одиниць; в) а сотень, 7 десятків і b одиниць; г) а тисяч, b сотень і а одиниць.
153. а) а сотень і b десятків; б) 5 сотень, а десятків і b одиниць. 154. Запишіть у вигляді виразу площу поверхні прямокутного паралелепіпеда з вимірами а см, b см, c см. 155.Запишіть у вигляді виразу площу поверхні куба з ребром а см.
Рис. 2 Рис. 3 156. Запишіть у вигляді виразу площу фігури, зображеної на рисунку 2. 157.Запишіть у вигляді виразу площу фігури, зображеної на рисунку 3. 158. На ділянці росло n кущів смородини. З цієї ділянки k кущів пересадили на іншу ділянку, а на ній посадили 30 нових кущів. Скільки кущів смородини стало на ділянці? Запишіть результат у вигляді виразу і знайдіть його значення, якщо n = 83, k = 45. 159. Оксана купила n олівців по 25 к. і 4 зошити по а к., заплативши за зошити більше, ніж за олівці. На скільки більше заплатила Оксана за зошити, ніж за олівці? Запишіть результат у вигляді виразу і знайдіть його значення, якщо n = 3, а = 65. 160. Із двох міст одночасно назустріч один одному виїхали два автомобілі й зустрілися через 2 год. Один рухався зі швидкістю 80 км/год, а інший ¾ зі швидкістю v км/год. Запишіть у вигляді виразу відстань між містами.
161. Число d є добутку перших n натуральних чисел: d = 1 × 2 × 3 × … × n. Знайдіть d, якщо n = 5; n = 7. Скількома нулями закінчується запис числа d, якщо n = 10; n = 100? 162. Знайдіть найменше значення виразу: х 2 + 5; | х | - 3. 163. Знайдіть найбільше значення виразу: 1 - х 2; 3 - | х |. 164. Запишіть формулу цілих чисел, які при діленні на 9 дають в остачі 2. Знайдіть кількість таких чисел у межах від 100 до 300. 165. Запишіть формулу цілих чисел, які при діленні на 2 дають в остачі 1, а при діленні на 3 дають в остачі 2. Вправи для повторення 166. Кавові зерна при смаженні втрачають 12% своєї маси. а) Скільки кілограмів смажених зерен вийде із 20 кг свіжих? б) Скільки кілограмів свіжих зерен слід узяти, щоб отримати 22 кг смажених? Обчисліть раціональним способом: 167. а) 0,25 × (-11) × 4; б) 9 × 1,25 × (-8); в) -12,5 × 2,5 × (-8) × 4; г) - є) 168. а) 34 × 23 + 3 × 23 - 37 × 33; б) 5,4 × 16 - 22 × 5,4 + 6 × 6,4. 169. Зведіть подібні доданки: а) 2 х + 6 х - 4 х + х; б) 4 a + 9 b + 2 b - 5 a; в) 3 a - 7 + 5 a - 10 a. 170. Розкрийте дужки: а) 4(a + 2 b); б) (a + b - c) × 3; в) 5(a - 1) - (b - c). 171. Візьміть у дужки два останніх доданки, поставивши перед дужками знак «+»; знак «–»: a) 2 х + у - 3; б) а - 3 b + 4; в) m + n - 7- mn.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 627; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.105.101 (0.012 с.) |

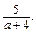 Значення цього виразу можна знайти для будь-якого значення а, крім а = -4. Якщо а = -4, то дільник (знаменник) а + 4 дорівнює нулю, а на нуль ділити не можна. Кажуть, що для а ¹ -4 вираз
Значення цього виразу можна знайти для будь-якого значення а, крім а = -4. Якщо а = -4, то дільник (знаменник) а + 4 дорівнює нулю, а на нуль ділити не можна. Кажуть, що для а ¹ -4 вираз 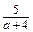 має зміст, а для а = -4 він не має змісту.
має зміст, а для а = -4 він не має змісту.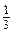 b,
b, 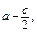
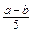
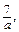 а: b,
а: b, 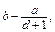
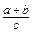 .
. Для тих, хто хоче знати більше
Для тих, хто хоче знати більше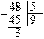
 Приклади розв’язання вправ
Приклади розв’язання вправ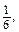 n =
n = 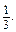
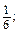 n =
n = 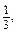 то
то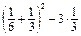 =
= 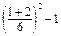 =
= 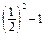 =
= 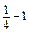 =
= 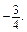
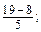 ж) abx 2.
ж) abx 2. є)
є) 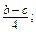 ж)
ж) 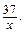
 Рівень А
Рівень А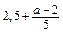 , якщо а = 4; б)
, якщо а = 4; б) 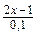 , якщо х = -3.
, якщо х = -3.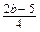
 Рівень Б
Рівень Б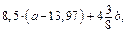 якщо a = 16,17; b =
якщо a = 16,17; b = 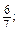
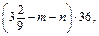 якщо m =
якщо m = 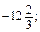 n =
n = 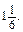
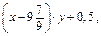 якщо х =
якщо х = 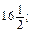 у =
у = 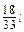
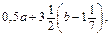 якщо а =
якщо а = 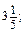 b = 2.
b = 2.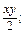 г)
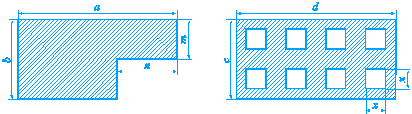
г) 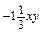 ?
?
 Рівень В
Рівень В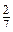 × (-25) ×
× (-25) × 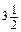 ; д) 24 × 8 - 28 × 24; е) 7 × 35 - 26 × 7 + 11 × 7;
; д) 24 × 8 - 28 × 24; е) 7 × 35 - 26 × 7 + 11 × 7;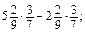 ж)
ж) 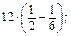 з)
з)