
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множення степенів з однаковими основами.Содержание книги
Поиск на нашем сайте
Розглянемо добутки двох степенів з основою а. Врахувавши, що а 1 = а, матимемо: а 1 а 1 = аa = а 2 = а 1 + 1; а 2 а 1 = (аа) a = ааа = а 3 = а 2 + 1. Отже, а 1 а 1 = а 1 + 1, а 2 а 1 = а 2 + 1. У цих прикладах добуток степенів з однаковими основами дорівнює степеню з тією ж основою і показником, який дорівнює сумі показників степенів. Таку властивість має добуток будь-яких степенів з однаковими основами.
amаn = аm + n . ● Доведення. Врахувавши означення степеня, матимемо: amаn = Із властивості 1, яку ще називають основною властивістю степеня, випливає правило множення степенів: Щоб перемножити степені з однаковими основами, потрібно основу залишити ту саму, а показники степенів додати. Наприклад: 32 × 33 = 32 + 3 = 35; 24 × 2 = 24 × 21 = 24 + 1 = 25; b 7 × b 8 = b 7 + 8 = b 15. Правило множення степенів поширюється на добуток трьох і більше степенів. Наприклад: 52 × 54 × 56 = 52 + 4 + 6 = 512; b 5 × b 3 × b 7 × b = b 5 + 3 + 7 + 1 = b 16. Ділення степенів з однаковими основами. Розглянемо рівність а 2 а 3= а 5, де а ¹ 0. Із цієї рівності за означенням а 5 : а 3 = а 5 - 3. У цьому прикладі частка степенів з однаковими основами дорівнює степеню з тією ж основою й показником, який дорівнює різниці показника степеня діленого й показника степеня дільника. Сформулюємо й доведемо відповідну властивість у загальному випадку.
аm : аn = аm - n . ● Доведення. Оскільки am - n × аn = аm - n + n = аm, тобто am - n × аn = аm, то за означенням частки маємо: аm : аn = аm - n . ● З доведеної властивості випливає правило ділення степенів: Щоб поділити степені з однаковими основами, потрібно основу залишити ту саму, а від показника степеня діленого відняти показник степеня дільника. Наприклад: 37: 32 = 37 - 2 = 35; х 4: х = х 4: х 1 = х 4 - 1 = х 3. Піднесення степеня до степеня. Піднесемо степінь а 2 до куба: (а 2)3 = а 2 × а 2 × а 2 = а 2 + 2 + 2 = а 2×3. Отже, (а 2)3 = а 2×3. Із прикладу видно: щоб піднести квадрат числа до куба, потрібно залишити ту ж основу й узяти показник, який дорівнює добутку показників. Сформулюємо й доведемо відповідну властивість у загальному випадку.
(am) n = аmn. ● Доведення. (am) n = Із властивості 3 випливає правило піднесення степеня до степеня: Щоб піднести степінь до степеня, потрібно основу залишити ту саму, а показники степенів перемножити. Наприклад: (43)5 = 43 × 5 = 415; (b 6)4 = b 6 × 4 = b 24. Піднесення добутку до степеня. Піднесемо добуток аb до куба: (аb)3 = аb × аb × аb = (аaa) × (bbb) = а 3 b 3. Отже, (аb)3 = а 3 b 3. Із прикладу видно: щоб піднести до куба добуток, потрібно піднести до куба кожний множник і результати перемножити.
(ab) n = аnbn. ● Доведення. (ab) n = Маємо таке правило: Щоб піднести до степеня добуток, досить піднести до цього степеня кожний множник і результати перемножити. Це правило поширюється на добуток трьох і більше множників. Наприклад: (5 ab)3 = 53 a 3 b 3 = 125 a 3 b 3; (abху) n = anbnхnуn. Зауваження. Доведені тотожності amаn = аm + n , аm : аn = аm - n , (am) n = аmn, (ab) n = аnbn, які виражають властивості степеня, дозволяють не тільки замінювати вирази, що стоять у їхніх лівих частинах, виразами, що стоять у правих частинах, а й навпаки: am + n = аmаn; am - n = аm: аn; аmn = (am) n = (an) m; аnbn = (ab) n.
Приклад 1. Спростити вираз (a 2 а)3 × (a 3 а 2)2. ● (a 2 а)3 × (a 3 а 2)2 = (a 3)3 × (a 5)2 = а 9 a 10 = a 19. ● Приклад 2. Обчислити: а) 0,36 : 0,34 + 0,14: 0,1; б) 2,55× 26× 0,45. ● а) 0,36 : 0,34 + 0,14: 0,1 = 0,32 + 0,13 = 0,09 + 0,001 = 0,091; б) 2,55× 26× 0,45 = (2,55× 0,45) × 26 = (2,5× 0,4)5× 26 = 15× 26 = 64. ● Приклад 3. Подати 418 у вигляді степеня з основою 42; 43; 46; 49. ● 418 = 42 × 9 = (42)9; 418 = (43)6; 418 = (46)3; 418 = (49)2. ● Приклад 4. Подати у вигляді степеня добуток а 6 b 6. ● а 6 b 6 = (аb)6. ● Усно 261. Подайте у вигляді степеня добуток: a) b 4 b 3; c 3 c; 72 × 75; 310 × 3; б) a 2 а 3 а 4; 2 × 23 × 24. 262. Подайте у вигляді степеня частку: a) а 6: а 2; b 8: b 3; б) 720: 717; 118: 11. 263. Піднесіть до степеня: a) (m 3)4; (n 10)2; (b 15)4; б) (pq)2; (2 b)3; (abc)4.
Подайте у вигляді степеня добуток: 264. a) a 5 а 2; б) b 4 b 6; в) yy 7; г) x 25 x 73; д) 28 × 212; е) 0,315 × 0,3; є) 53 × 5 × 54; ж) 34 × 3 × 36 × 3; з) b 5 bb 2 b 4. 265. a) m 3 m 6; б) y 7 y 5; в) c 5 c; г) b 15 b 25; д) 105 × 1010; е) 2,5 × 2,53; є) 2 × 22 × 27; ж) a 2 a 4 aa 2. Подайте у вигляді степеня частку: 266.a) х 10: х 3; б) а 15: а 5; в) 528: 521; г) 0,18: 0,12. 267. a) с 12: с 9; б) b 26: b 8; в) 417: 415; г) 0,710: 0,74. 268. Подайте степінь b 15 у вигляді добутку двох степенів з основою b чотирма способами. 269.Подайте степінь х 12 у вигляді добутку двох степенів, одним з яких є: х; х 2; х 4; х 7; х 9. 270. а) Подайте у вигляді степеня з основою b:(b 3)3;(b 4)5; (b 5)7; (b 25)4. б) Подайте у вигляді степеня з основою ab: a 3 b 3; a 5 b 5. 271. а) Подайте у вигляді степеня з основою m: (m 5)3; (m 2)7; (m 5)4. б) Подайте у вигляді степеня з основою mn: m 2 n 2; m 7 n 7. Піднесіть до степеня: 272. а) (ab)5; б) (4 c)2; в) (-2 x)3; г) (-0,1 a)2; д) (3 xy)3; е) (-2 mn)5; є) (mnk)8; ж) (4 abcd)4. 273. а) (st)7; б) (-3 b)3; в) (-2 mn)4; г) (5 klm)3. Знайдіть значення виразу: 274. а) 58 : 55; б) 0,29 : 0,27; в) (-2)7 : (-2)4; г) (32)3 : 34; д) 87 : 85 - 32 × 3; е) 1,59 : 1,58 - 0,52. 275. а) 418 : 415; б) 0,58 : 0,56; в) 35 : 32 + 46 : 44; г) (102)2 - 56 : 53.
Подайте у вигляді степеня: 276. а) 24 × 16; б) 37 : 27; в) 0,54 × 0,25; г) 0,001 × 0,15. 277. а) 93 × 81; б) 64 × 23; Знайдіть значення виразу: 278. а) 24 × 54; б) 43 × 253; в) 0,56 × 26; г) 1,255 × 25 × 45; д) є) (0,518: 0,56) × (216: 24); ж) 279. а) 53 × 23; б) 82 × 1252; в) 0,259 × 29 × 29; г) д) (278: 95) : (94 × 32); е) 280. а) Подайте z 20 у вигляді степеня з основою z 2; z 4; z 5; z 10. б) Подайте 220 у вигляді степеня з основою 4; 16; 32. 281. а) Подайте c 12 у вигляді степеня з основою с 2; с 3; с 4; с 6. б) Подайте 312 у вигляді степеня з основою 9; 27; 81. 282. Подайте у вигляді степеня з основою а: a) ama 2; б) aak; в) (am)2; г) (a 3) k. Спростіть вираз: 283. а) (а 3 a 4)5; б) (a 7 : а)3; в) (а 2)3 × (а 4)4; г) (а 5)5 : (аа 4)2. 284. a) (a 5 a 6)2; б) (a 8 : a 5)5; в) (a 4)2 × (a 2)4; г) (a 6)3 : (a 3)2.
285. Подайте у вигляді степеня з основою а: а) 286. Доведіть, що куб натурального числа, кратного 3, ділиться на 27. 287. Що більше: 2300 чи 3200? 288. Обчисліть: 289. Доведіть, що значення виразу 4343 × 4243 – 3333 × 3733 ділиться на 5. Вправи для повторення 290. Спростіть вираз: а) 2 х - 3 – (3 х + 1); б) 6 а + 3 – 2(а – 2); в) –2(b - 1) + 3(5 - 2 b) – 17; г) 5(-3 c + 5) + 4(3 – c) – 4 + 19 c. 291. Скільки одержимо числових виразів, якщо у виразі 2 х - 5 у змінній х надаватимемо значень 1, 3, 5, 7 або 9, а змінній у — значень 2, 4, 6 або 8? 292. Автомобіль проїхав деякий шлях за 1,5 год, рухаючись зі сталою швидкістю. Якби він їхав на 12 км/год швидше, то проїхав би цей шлях за 1,3 год. Який шлях проїхав автомобіль? 293. З басейну через дві труби випустили 450 м3 води за 50 хв. Щохвилини через першу трубу виливалося води в 1,25 разу більше, ніж через другу. Скільки води витекло через першу трубу?
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1831; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.01 с.) |

 =
=  = аm + n . ●
= аm + n . ● =
=  = аmn. ●
= аmn. ● =
= 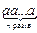 ×
×  = аnbn. ●
= аnbn. ● Приклади розв’язання вправ
Приклади розв’язання вправ Рівень А
Рівень А Рівень Б
Рівень Б е) 163: (412: 84);
е) 163: (412: 84);

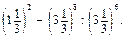
 Рівень В
Рівень В б)
б) 
 г)
г) 




