
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одночлен та його стандартний виглядСодержание книги
Поиск на нашем сайте
1. Одночлени. Розглянемо дві групи виразів: а, b 3, 5, 32, 9 аb 2, -2 x 4 y 3, і 3 + 2 а, а - b, 5 + х 2. Яка особливість виразів першої групи? Чим вони відрізняються від виразів другої групи? Вирази першої групи ¾ це змінні, числа, їхні степені й добутки. Такі вирази називають одночленами. У загальному вигляді одночлен ¾ це добуток чисел, змінних та їхніх степенів. Вирази другої групи не є одночленами, бо містять дії додавання або віднімання. Розглянемо одночлен -4 а 2 b 3. Він містить тільки один числовий множник, який стоїть на першому місці, і степені різних змінних. Такий одночлен називають одночленом стандартного вигляду. Одночленом стандартного вигляду називають такий одночлен, який містить тільки один числовий множник, що стоїть на першому місці, і степені різних змінних. Числовий множник одночлена стандартного вигляду називають коефіцієнтом одночлена. Коефіцієнт одночлена -4 а 2 b 3 дорівнює -4. Вважають, що коефіцієнти одночленів а 3 і - bс відповідно дорівнюють 1 і -1, бо а 3 = 1 × а 3 і - bс = -1 × bс. Одночлен 5 а 3 b 2 а 4 не є одночленом стандартного вигляду, бо містить два степені з основою а. Помноживши а 3на а 4, цей одночлен можна записати у вигляді одночлена стандартного вигляду: 5 а 3 b 2 а 4 = 5(а 3 а 4) b 2 = 5 а 7 b 2. 2. Множення одночленів. Перемножимо одночлени -3 а 2 b і 4 аb 3. Використовуючи властивості дії множення і властивості степенів, матимемо: -3 а 2 b × 4 аb 3 = (-3 × 4) × (а 2 а)× (bb 3) = -12 а 3 b 4. Отже, добутком одночленів -3 а 2 b і 4 аb 3 є одночлен -12 а 3 b 4. Взагалі, добутком будь-яких одночленів є одночлен. 3. Піднесення одночлена до степеня. Піднесемо одночлен -5 а 2 b до куба. Використовуючи властивості степенів, матимемо: (-5 а 2 b)3 = (-5)3 × (а 2)3× b 3 = -125 а 6 b 3. Отже, кубом одночлена -5 а 2 b є одночлен -125 а 6 b 3. Взагалі, натуральним степенем будь-якого одночлена є одночлен. 4. Степінь одночлена. В одночлена 3 а 2 bх 3 сума показників степенів усіх змінних дорівнює 2 + 1 + 3 = 6. Цю суму називають степенем одночлена, кажуть, що 3 а 2 bх 3 ¾ одночлен шостого степеня. Степенем одночлена називають суму показників степенів усіх змінних, що входять до нього. Якщо одночленом є число, то вважають, що степінь такого одночлена дорівнює нулю. Наприклад: - а 2 b 7 ¾ одночлен дев’ятого степеня; 2 а 2 ¾ одночлен другого степеня; 3 х ¾ одночлен першого степеня;-2 ¾ одночлен нульового степеня.
Приклад 1. Записати вираз у вигляді одночлена стандартного вигляду: а) 6 аb 2× (-4 аb); б) -3 а 3 b × 4 а 2 с × 3 с 3; в) (- x 2 y × 4 xy 2)3. ● а) 6 аb 2× (-4 аb) = (6× (-4)) × (аа) × (b 2 b) = -24 а 2 b 3. Скорочений запис: 6 аb 2× (-4 аb) = -24 а 2 b 3. б) -3 а 3 b × 4 а 2 с × 3 с 3 = (-3 × 4× 3) × (а 3 а 2)× b × (сс 3) = -36 а 5 bс 4. Скорочений запис: -3 а 3 b × 4 а 2 с × 3 с 3 = -36 а 5 bс 4. в) (- x 2 y × 4 xy 2)3 = (-4 x 3 y 3)3 = -64 x 9 y 9. ● Приклад 2. Подати одночлен 4 a 4 b 6 у вигляді: а) добутку двох одночленів стандартного вигляду; б) добутку двох одночленів, одним з яких є 2 a 2 b 2; в) квадрата одночлена стандартного вигляду. ● а) 4 a 4 b 6 = 4 a 2 b 4 × a 2 b 2 (або 4 a 4 b 6 = 4 a 4 × b 6, 4 a 4 b 6 = -2 ab × (-2 a 3 b 5) тощо); б) 4 a 4 b 6 = 2 × 2 × a 2 × a 2 × b 2 × b 4 = 2 а 2 b 2 × 2 а 2 b 4; в) 4 a 4 b 6 = (2 a 2 b 3)2. ● Усно 294. Які з наведених виразів є одночленами: a) д) - m; е) 0,3; є) 3 a 3 bc 3 ab; ж) b? 295. Назвіть одночлени стандартного вигляду та їхні коефіцієнти: 2 a 2 ba; 52 аb; 0,03 ас 4; x; - y; 1,4 a; 4,8; 5 ab × 3 cd. 296. Знайдіть степінь одночленів: 4 a 2 b 2; x 3 y 5; 0,1 a 2 b 3 с 4; 7 xy 2; 6 a 2; - y 3; 4 a; cd; 15. 297. Перемножте одночлени: a) 2 a і 3 b; б) 4 с 2 і 2 с; в) 5 a 2 b і ab; г) - хy 2 і 2 x.
Подайте одночлен у стандартному вигляді та вкажіть його степінь і коефіцієнт: 298. a) 4 x 2 yx; б) 5 abc × (-2); в) 0,4 а 2 × 4 а 3 b; г) 299. a) 14 y 5 y; б) -0,3 cc 3 c; в) Виконайте множення одночленів: 300. а) 5 a × 4 b; б) -3 а 2 × 5 а 3; в) 0,3 а 2 b × 2 b; г) -4 ax 2 × 3 bx 3; д) є) -4,3 ax × (-2 a 2) × 5 x; ж) xy × (-5 xy 2) × (-4); з) -3 cd × (-2 dc 2) × cd. 301. а) 2 m × 12 mn 5; б) - cd × 8 c 4 d; в) 7 a 3 b 2 c × 0,8 abc 3; г) -6 n 3 k × Піднесіть одночлен до степеня: 302. а) (3 a 3 b)3; б) (-2 mn 2)4; в) 303. а) (-5 mn 2)2; б) (3 a 3 b 6)3; в) (- xy 2 z 3)5; г) (2 ab 4 c 3)4. 304. Подайте одночлен 8 х 2 у 3 у вигляді: а) добутку двох одночленів стандартного вигляду; б) добутку двох одночленів, одним з яких є: 4 х 2 у 2; 8 ху; -2 ху 3. 305.Подайте одночлен 6 b 3 c 3 у вигляді: а) добутку двох одночленів стандартного вигляду; б) добутку двох одночленів, одним з яких є: 2 b 2 c 2; 6 bc; -3 bc 3.
Спростіть вираз: 306. а) в) д) 307. а) в) (- a 2 b)3 × (-3 a 3 b)2; г) 308. Як зміниться площа квадрата, якщо його сторону збільшити втричі? 309.Як зміниться об’єм куба, якщо його ребро збільшити удвічі? 310. Подайте одночлен 64 a 6 b 18 у вигляді: а) добутку двох одночленів стандартного вигляду; б) добутку трьох одночленів стандартного вигляду; в) добутку двох одночленів, одним з яких є -4 a 4 b 6; г) квадрата одночлена стандартного вигляду; д) куба одночлена стандартного вигляду. 311.Подайте одночлен 16 x 12 y 8 у вигляді: а) добутку трьох одночленів стандартного вигляду; б) добутку двох одночленів, одним з яких є -2 x 3 y 7; в) квадрата одночлена стандартного вигляду; г) четвертого степеня одночлена стандартного вигляду. 312. Для деяких значень змінних значення виразу m 2 n 3 дорівнює 2. Знайдіть для тих же значень змінних значення виразу: а) 6 m 2 n 3; б) m 4 n 6; в) 4 m 8 n 12; г) -3 m 6 n 9. Знайдіть значення виразу: 313. а) (2 а 2 b)2 × аb 3, якщо а = 2; b = 5; б) (xy 2 z)3 × xzy 8, якщо x = в) (a 2 bc 2)2 × abc × b 2, якщо a = 314. а) (- mn 2)3 × 10 m 4 n, якщо m = 4; n = 0,25; б) (2 abc 4)2 × 0,25(ab)6, якщо a =
315. Подайте одночлен у стандартному вигляді: a) в) 316. Знайдіть значення виразу: а) б) 317. Мило має форму прямокутного паралелепіпеда. За тиждень користування всі його розміри зменшились удвічі. У скільки разів зменшився об’єм мила? Вправи для повторення 318. Розв’яжіть рівняння: а) 2(х – 1) + 3(2 – х) = 2; б) 319. Розкрийте дужки і зведіть подібні доданки: а) 7 с - 5 + (3 с + 1 - 8 с); б) 2 а + 8 – (3 а + 12 – 6 а); в) (-2 b + 4) – (4 b - 1) + 6 b; г) (-3 x + 5) - (3 – x) - (2 + 2 x). 320. Для купівлі телевізора сім’я відкладала щомісяця одну й ту ж суму 321. З міста А до міста В вийшов поїзд і йшов зі швидкістю 60 км/год, а через 3 год назустріч йому з міста В вийшов другий поїзд і йшов швидкістю 75 км/год. Коли поїзди зустрілися, з’ясувалося, що перший пройшов на 105 км більше, ніж другий. Знайдіть відстань між містами А і В. 322*. Числа а і b задовольняють умови: a > 0; a + b < 0. а) Знайдіть знак числа b. б) Що більше: | а | чи | b |?
Поняття степеня з натуральним показником виникло ще в античні часи у зв’язку з обчисленням площ і об’ємів. Тлумачення степенів а 2 і а 3 було геометричним: а 2 — це площа квадрата зі стороною а, а 3 — об’єм куба з ребром а. Звідси і назви «квадрат» і «куб» для степенів а 2 і а 3, які використовуються й досі. Щоправда, така геометрична прив’язка в ті часи послужила гальмом для розвитку алгебри. Степені а 4 («квадрато-квадрат»), а 5 («кубо-квадрат») і т. д. залишалися ніби «поза законом», оскільки не мали відповідного геометричного підґрунтя. Лише у XVII ст. французький математик Рене Декарт (1596–1650) дав геометричне тлумачення добутку довільної кількості множників, після чого й добуток Запитання і вправи для повторення § 3 1. Що називають степенем числа з натуральним показником? 2. Наведіть приклад степеня з натуральним показником та назвіть його основу й показник. 3. Який знак має степінь з натуральним показником залежно від знака основи?
4. Сформулюйте й доведіть основну властивість степеня. 5. Сформулюйте й доведіть правила множення та ділення степенів з однаковими основами, піднесення добутку до степеня та піднесення степеня до степеня. 6. Наведіть приклади одночленів. З чого складається одночлен? 7. Який одночлен називають одночленом стандартного вигляду? Наведіть приклад такого одночлена. 8. Як знайти степінь одночлена? 323. Знайдіть значення степеня: а) 104; б) (-3)6; в) (-0,5)3; г) (-2,4)3; д) 1,024; е) 324. Обчисліть: а) (-4) × 24; б) (-4) × (-24); в) 52 × (-2)3; г) 53 × (-63); д) (72 - 32)2; е) (-4 × 1,5 + 8)5; є) 28 + (-2)5; ж) (-0,125 × 23)15. 325. Знайдіть значення виразу: а) а 4 - 81, якщо а = -3; 0; 3; б) (2 х - 3)3, якщо х = -1; 3. 326. а) Подайте у вигляді квадрата число: 64; 169; 1,44; 0,0001; б) Подайте у вигляді куба число: 64; 1000; -27; 0,008; Подайте вираз у вигляді степеня: 327. a) a 3 а 5; б) b 9: b 8; в) yy 8; г) a 5 aa 4; д) 64 × 621; е) (p 2)5; є) (75)4; ж) (53 : 5)7. 328. Подайте степінь 324 у вигляді добутку двох степенів, одним з яких є: 32; 34; 39; 315. 329. а) Подайте степінь а 36 у вигляді степеня з основою а 2; а 3; а 9; а 12. б) Подайте степінь 418 у вигляді степеня з основою 2; 16; 8. 330. Піднесіть одночлен до степеня: а) (ху)4; б) (6 а)3; в) (-3 x 2)4; г) (-0,5 a 4 с 2)2. 331. Подайте одночлен у стандартному вигляді та вкажіть його степінь: a) -2 a 4 ba; б) 0,5 b 2 × 2 а 3 b; в) -3 x 3 × г) -4 a 2 × 7 а 5 b × 4 b 3; д) 2,5 xz × (-4 x 3 z 3) × x 2 z; е) (3 a 3 b 4 c 5 d)4; є) 332. Подайте одночлен 49 a 4 b 12 у вигляді: а) добутку двох одночленів стандартного вигляду; б) добутку двох одночленів, одним з яких є -7 a 3 b 7; в) квадрата одночлена стандартного вигляду. 333. Знайдіть значення виразу: а) (3 х 2 у)3 × у 3, якщо х = 2; у = 0,5; б) (a 2 bc)2 × 5 abc 3, якщо a = 334*. Спростіть вираз: а) (a 4)2 n × (a 4 an + 2)2; б) (-2 yk)8 × (- y 3)5; в) 335*. Якою цифрою закінчується число 381? 336*. Що більше: 8020 чи 940? 337*. Розв’яжіть рівняння: а) (2 х)2 +(256 х)8 = 0; б) (х - 2)2 + (х + 2)2 = 0; в) х 6 + |3 х | = 0. Завдання для самоперевірки № 3 Рівень 1. Яка з рівностей є правильною: а) 3× 3× 3× 3× 3 = 5 × 3; б) 3× 3× 3× 3× 3 = 53; в) 3× 3× 3× 3× 3 = 35? 2. Вкажіть правильну рівність: а) 25 = 10; б) 25 = 32; в) 25 = 25; г) 25 = 16. 3. Вкажіть правильну рівність: а) 24× 23 = 212; б) 24× 23 = 412; в) (32)3 = 63; г) (32)3 = 36. 4. Подайте одночлен -3 х 2 ух 5 у стандартному вигляді: a) -3 ух 2 х 5; б) -3 х 10 у; в) -3 х 7 у; г) -3(ху)7. 5. Виконайте множення 2 а 2 b 3 × 3 a 4 і вкажіть правильну відповідь: а) 6 a 2 b 7; б) 6 a 8 b 3; в) 5 a 6 b 3; г) 6 a 6 b 3. Рівень 1. Запишіть вираз у вигляді степеня з основою х: а) х 5× х 3; б) х 4× х; в) (х 5)3; г) (х 6)4. 2. Обчисліть:
а) 4× 33 - 43; б) (25 - 42)× 5; в) (32 + 1)3. 3. Подайте одночлен у стандартному вигляді: a) 2 a 4 × 3 a; б) -0,3 аb 3 × 5 a 4 b 2; в) (2 аc 3)4. 4. Знайдіть значення виразу: а) (2 ху)3, якщо х = 2; у = 0,25; б) (a 2 b)2 × ab 2, якщо a = 2; b = 5. Рівень 1. Запишіть вираз у вигляді степеня: а) (63× 64)5× 6; б) (35× 3)3× (34)7; в) 28× 44 × 162. 2. Спростіть вираз: a) 3,6 x 2 у 2 × (-5 x 4 у 5) × (-2 x 2 у); б) в) (- m 7 n 8)5 × (-0,2 m 3 n 5)4; г) 3. Подайте одночлен 64 a 12 b 18 у вигляді: а) добутку трьох одночленів стандартного вигляду; б) добутку двох одночленів, одним з яких є -4 a 5 b 8; в) куба одночлена стандартного вигляду. 4. Знайдіть значення виразу: а) (а 4 с 2)2 × с 4, якщо а = 4; с = -0,5; б) 2(x 2 yz 3)2 × x 2 y 2, якщо x = Рівень 1. Запишіть вираз у вигляді степеня з основою 2: а) 2. Знайдіть значення виразу: а) (8 m 3 n 2)2 × n 2, якщо m = 20; n = -0,025; б) 3. Якою цифрою закінчується число 445? 4. Розв’яжіть рівняння: а) (4 х)4 + (-8 х)8 = 0; б) х 2 + |2 х - 1| = 0. МНОГОЧЛЕНИ
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.202 (0.013 с.) |

 m 2 n
m 2 n Приклади розв’язання вправ
Приклади розв’язання вправ б) -3 abc; в)
б) -3 abc; в)  ; г) а + b;
; г) а + b; Рівень А
Рівень А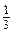 x 3 y 2 × 3 x; д) -5 c 3 d × 0,8 c 2 d; е) 0,7 c × 4 с × с 2; є) -6 аbс ×
x 3 y 2 × 3 x; д) -5 c 3 d × 0,8 c 2 d; е) 0,7 c × 4 с × с 2; є) -6 аbс ×  аb × 3 а 2; г) 0,5 aa 3 × 2 aa 2.
аb × 3 а 2; г) 0,5 aa 3 × 2 aa 2.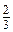 m 3 n × (-6 mn 2); е) 8 а 2 bc 2 ×
m 3 n × (-6 mn 2); е) 8 а 2 bc 2 ×  ;
; k; д) - ab × (-5 ab 2) × 2 b; е) 1,5 xy × (-2 x 2 y 3) × x 2 y.
k; д) - ab × (-5 ab 2) × 2 b; е) 1,5 xy × (-2 x 2 y 3) × x 2 y. г) (-0,5 mn 3 k 4)2.
г) (-0,5 mn 3 k 4)2. Рівень Б
Рівень Б б) (3 а 2 b)3 × 0,01 b 2;
б) (3 а 2 b)3 × 0,01 b 2; г) (-4 a 2 b 3)2 × (- ab 3)2;
г) (-4 a 2 b 3)2 × (- ab 3)2; е)
е) 
 б)
б) 

 y = -1; z = 7;
y = -1; z = 7; b = -0,5; c = 3.
b = -0,5; c = 3. b = 14; c = -0,1.
b = 14; c = -0,1. Рівень В
Рівень В б)
б) 
 г)
г) 
 якщо х =
якщо х =  у = 2; n = 80;
у = 2; n = 80; , якщо а = 0,1; b = 2; k = 51.
, якщо а = 0,1; b = 2; k = 51.
 набув «офіційного статусу». Декарт же увів і сучасне позначення степеня з натуральним показником у вигляді ап.
набув «офіційного статусу». Декарт же увів і сучасне позначення степеня з натуральним показником у вигляді ап. є)
є)  ж)
ж) 




 ж)
ж)  з) (-4 m 2 n 5)3 × (-2 mn 3)2.
з) (-4 m 2 n 5)3 × (-2 mn 3)2. b = -4; c =
b = -4; c = 
 г)
г) 
 а 2 с 3 × (3 a 2 b 4 c 3)3;
а 2 с 3 × (3 a 2 b 4 c 3)3;
 y = -2; z =
y = -2; z = 
 б)
б) 
 якщо а =
якщо а =  b =
b =  k = 18.
k = 18.


