
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування систем лінійних рівнянь способом додаванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо дві правильні рівності: 7 + 5 = 12; 8 + 6 = 14. Додамо почленно ці рівності: ліву частину до лівої й праву до правої: (7 + 5) + (8 + 6) = 12 + 14. Знову одержали правильну рівність. Ця властивість правильних числових рівностей лежить в основі способу розв’язування систем рівнянь, який називають способом додавання. Розглянемо приклад. Нехай треба розв’язати систему рівнянь
Додамо почленно ліві й праві частини рівнянь: (3 х + 2 у) + (5 х – 2 у) = 21 + 19; 8 х = 40. Замінимо одне з рівнянь системи (1), наприклад, перше, рівнянням 8 х = 40. Одержимо систему
Системи (1) і (2) мають одні й ті ж розв’язки (доведення подане в рубриці «Для тих, хто хоче знати більше»). Розв’яжемо систему (2). З першого 5 × 5- 2 у = 19; 25- 2 у = 19; -2 у = -6; у = 3. Пара чисел (5; 3) ¾ розв’язок системи (2), а також і системи (1). Розв’язуючи систему (1), ми скористалися тим, що в рівняннях коефіцієнти біля змінної у є протилежними числами і після почленного додавання рівнянь одержали рівняння з однією змінною х. Розв’яжемо ще одну систему рівнянь
У цій системі рівнянь коефіцієнти біля змінної х і коефіцієнти біля змінної у не є протилежними числами. Однак, помноживши обидві частини першого рівняння на 2, а другого ¾ на -3, одержимо систему
у якій коефіцієнти біля х ¾ протилежні числа. Додавши почленно рівняння останньої системи, матимемо: 17 у = 102; у = 6. Підставивши значення y в перше рівняння системи (3), знаходимо: 3 х + 4 × 6 = 12; 3 х = -12; х = -4. Отже, розв’язком системи (3) є пара чисел (-4; 6).
Доведемо, що системи (1) і (2) мають одні й ті ж розв’язки. Нехай пара чисел (a; b) ¾ довільний розв’язок системи (1), тоді правильними є числові рівності 3 а + 2 b = 21 і 5 а - 2 b = 19. Додавши ці рівності, одержимо правильну рівність 8 а = 40. Оскільки рівності 8 а = 40 і 5 а - 2 b = 19 правильні, то пара чисел (a; b) є розв’язком системи (2). Ми показали, що довільний розв’язок системи (1) є розв’язком системи (2).
Навпаки, нехай пара чисел (с; d) ¾ довільний розв’язок системи (2), тоді правильними є числові рівності 8 c = 40 і 5 c - 2 d = 19. Віднімемо від першої із цих рівностей другу. Одержимо правильну рівність 3 c + 2 d = 21. Оскільки рівності 3 c + 2 d = 21 і 5 c - 2 d = 19 правильні, то пара чисел (c; d) є розв’язком системи (1). Ми показали, що довільний розв’язок системи (2) є розв’язком системи (1). Отже, системи (1) і (2) мають одні й ті ж розв’язки.
Приклад 1. Розв’язати способом додавання систему рівнянь
● Помножимо обидві частини першого рівняння системи на -2. Отримаємо систему
Почленно додавши рівняння останньої системи, матимемо: -3 у = -9; у = 3. Підставимо у перше рівняння системи замість у число 3 і розв’яжемо одержане рівняння: 3 х + 15 = 9; 3 х = -6; х = -2. Відповідь. (-2; 3). ●
Розв’яжіть систему рівнянь способом додавання: 973. а) 974. а) 975. а) 976. а) г) 977. а) в)
Знайдіть розв’язки системи рівнянь: 978. а) в) 979. а) 980. а) в) 981. а) 982. Чи має розв’язок система рівнянь: а)
983. Чи має розв’язок система рівнянь: а) 984. Доведіть, що графіки рівнянь 6 х + 5 у = -7, 2 х - 3 у = 7 і 4 х + у = 0 проходять через одну й ту ж точку. 985. Розв’яжіть систему рівнянь: а) в) 986. Скільки розв’язків має система рівнянь 987. Знайдіть такі числа a, b, c і d, для яких є правильною кожна з рівностей: а = bcd; a + b = cd; a + b + c = d; a + b + c + d = 1. Вправи для повторення 988. Запишіть відповідні рівності: а) сума чисел x та у у 5 разів більша від їх різниці; б) добуток чисел а і b на 12 більший від їх частки; в) сума чисел x та у становить третину їх добутку. 989. Одне число більше від іншого втричі, а їхня сума дорівнює 36. Знайдіть ці числа. 990. Знайдіть два числа, сума яких дорівнює 49, а різниця ¾ 17. 991. Брат старший від сестри удвічі. А 5 років тому він був старший від сестри на 7 років. Скільки років кожному? 992. Вкладник зняв з рахунку в банку 20% усіх грошей, а через годину ¾ 30% залишку. Після цього на його рахунку залишилося 280 грн. Який був початковий вклад?
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 880; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.4.65 (0.009 с.) |

 (1)
(1) (2)
(2) (3)
(3)
 Для тих, хто хоче знати більше
Для тих, хто хоче знати більше Приклади розв’язання вправ
Приклади розв’язання вправ

 Рівень А
Рівень А б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 д)
д)  е)
е) 
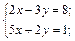 б)
б) 
 г)
г) 
 Рівень Б
Рівень Б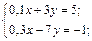 б)
б) 
 г)
г) 
 б)
б) 
 б)
б) 
 г)
г) 
 б)
б) 
 б)
б) 
 Рівень В
Рівень В б)
б) 
 б)
б) 
 г)
г) 
 залежно від значень коефіцієнта а?
залежно від значень коефіцієнта а?


