Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розкладання на множники різниці квадратів двох виразівСодержание книги
Поиск на нашем сайте
У тотожності (a - b)(a + b) = a 2 - b 2 поміняємо місцями ліву і праву частини: a 2 - b 2 = (a - b)(a + b). Одержану тотожність називають формулою різниці квадратів двох виразів. Формулюють її так:
Формула різниці квадратів дає можливість розкласти на множники двочлен a 2 - b 2. Її використовують для розкладання на множники різниці квадратів двох довільних виразів. Наприклад: 4 х 2 - 9 = (2 х)2 - 32 = (2 x - 3)(2 x + 3). Порівняйте
Приклад 1. Розкласти на множники: а) 16 х 4 - 2,25 у 2 z 2; ● а) 16 х 4 - 2,25 у 2 z 2 = (4 х 2)2 - (1,5 уz)2 = (4 х 2 - 1,5 уz)(4 х 2 + 1,5 уz); б) (4 a - b)2 - a 2 = (4 a - b - a)(4 a - b + a) =(3 a - b)(5 a - b). ● Приклад 2. Обчислити 752 - 652. ● 752 - 652= (75- 65)(75 + 65)= 10 × 140 = 1400. ● Приклад 3. Розв’язати рівняння (х - 3)2- 36= 0. ● (х - 3)2- 36= 0; (х - 3)2- 62= 0; (х - 3- 6)(х - 3 + 6)= 0; (х - 9)(х + 3) = 0; х - 9 = 0 або х + 3 = 0; х = 9 або х = -3. Відповідь. 9; -3. ● Усно 605. Розкладіть на множники: a) x 2 - y 2; б) p 2 - 4; в) 16 - c 2.
Розкладіть на множники: 606. a) a 2 - 9; б) b 2 - 1; в) 1 – x 2; г) 16 - y 2; д) 4 z 2 – 36; е) 49 a 2 - 9 b 2; є) 100 x 2 - 121 y 2; ж) 9 - a 2 b 2. 607. a) b 2 - 25; б) 9 c 2 - 1; в) 25 - 64 y 2; г) 36 m 2 - 49 n 2; д) 400 - z 2; е) 81 p 2 - 121 q 2. Обчисліть: 608. a) 452 - 442; б) 812 - 712; в) 1382 - 382; г) 6,72 - 3,32. 609. а) 292 - 282; б) 2052 - 1052; в) 782 - 222; г) 9,52 - 8,52. Знайдіть значення виразу: 610. x 2 - y 2, якщо x = 42 і y = 32; x = 2,8 і y = 7,2; x = 54 і y = -46. 611. m 2 - n 2, якщо m = 116 і n = 16; m = 5,7 і n = -4,7. Розв’яжіть рівняння: 612. а) x 2- 4 = 0; б) 25 x 2 - 16 = 0.
Рівень Б Розкладіть на множники: 614. а) а 4 - b 2; б) 25 m 2 - 64 n 8; в) 36 - 4 а 6 с 2; г) 0,01 - 6,25 х 8 у 10; д) 615. а) 4 a 8 - 25 b 2 c 2; б) 1,96 m 20 - 0,09 n 2; в) 616. а) (a + 2)2 - 1; б) (3 b - 1)2 - 4; в) 16 - (3 b + 2)2; г) (2 a - 5)2 - 25 b 2; д) (4 x + 3)2 - (3 x + 2)2; е) (a - 3 b)2 - (3 a + 5 b)2. 617. а) (2 х - 1)2 - 9; б) 4 a 2 - (4 a + 3)2; в) (4 х - y)2 - (5 x - 2 y)2. Знайдіть значення виразу: 618. а 2 - 4 b 2, якщо a = 3,28 і b = 3,36; a = 619.9 p 2 - q 2, якщо p = 2,3 і q = -1,9; p = Розв’яжіть рівняння: 620. а) (x + 3)2 - 1 = 0; б) (5 y - 2)2 - 9 = 0; в) (3 z + 5)2 - 4 z 2 = 0; г) (2 x - 3)2 - (3 x + 3)2 = 0. 621. а) (2 x - 5)2 - 1 = 0; б) (4 y - 7)2 - (y + 2)2 = 0. 622. Доведіть, що значення виразу ділиться на дане число: а) 45752 - 14252 на 1000; б) 8432 - 2572 на 200.
623. Візьмемо два числа a і b, що дорівнюють одне одному: a = b. Обидві частини рівності помножимо на a і потім віднімемо від обох частин b 2. Отримаємо: a 2 = ab; a 2 – b 2 = ab – b 2; (a + b)(a – b) = b (a – b). Звідси a + b = b. З одержаної рівності, врахувавши, що a = b, матимемо: b + b = b; 2 b = b; Отже, отримали, що будь-яке число дорівнює своїй половині. Знайдіть помилку в проведених міркуваннях. 624. Доведіть, що для будь-якого цілого значення k значення виразу (4 k + 2)2 - (4 k - 2)2 ділиться на 32. 625. Розкладіть на множники: а) a 8 - b 8; б) 1 - х 16. 626. Розв’яжіть рівняння: а) x 4- 16 = 0; б) x 8 – 1 = 0; в) (х 2 + 4 х - 7)2 - (х 2 + 4 х + 7)2 = 0. 627. Доведіть, що різниця квадратів двох цілих чисел, одне з яких при діленні на 5 дає в остачі 3, а інше ¾ 2, кратна 5. Вправи для повторення 628. Обчисліть: а) 629. Батькові 36 років, а синові ¾ 12. а) Через скільки років батько буде удвічі старший від сина? б) Скільки років тому батько був у 5 разів старший від сина? 630. З міста А до міста В, відстань між якими дорівнює 250 км, виїхав автобус. Через 40 хв з міста В назустріч йому виїхав автомобіль, швидкість якого на 20 км/год більша від швидкості автобуса. Через 1,5 год після виїзду автомобіля він зустрів автобус. Яка швидкість автомобіля? 631. Піднесіть до квадрата: а) (m – 5)2; б) (3 a + 1)2; в) (4 b – 3)2; г) (–2 a – 5 b)2. 19. Розкладання многочленів на множники з використанням Запишемо формули квадрата суми і квадрата різниці двох виразів (квадрата двочлена), помінявши в них ліві та праві частини: a 2 + 2 ab + b 2 = (a + b)2 = (a + b)(a + b); a 2 - 2 ab + b 2 = (a - b)2 = (a - b)(a - b). Перша із цих формул дає розклад на множники тричлена a 2 + 2 ab + b 2, а друга ¾ тричлена a 2 - 2 ab + b 2.
Приклад 1. Розкласти на множники тричлен 9 a 2 - 24 ab + 16 b 2. ● 9 a 2 - 24 ab + 16 b 2 = (3 a)2 - 2 × 3 a × 4 b + (4 b)2 = (3 a - 4 b)2. ● Приклад 2.Знайти значення виразу x 2 + 8 x + 16, якщо x = 16; x = -11. ● Запишемо спочатку тричлен x 2 + 8 x + 16 у вигляді квадрата двочлена: x 2 + 8 x + 16 = (х + 4)2. Якщо х = 16, то: (х + 4)2 = (16+ 4)2 = 202 = 400. Якщо х = -11, то: (х + 4)2 = (-11+ 4)2 = (-7)2 = 49. ● Усно 632. Розкладіть на множники: а) x 2 + 2 xy + y 2; б) x 2 - 2 xb + b 2; в) x 2 + 2 x + 1.
Подайте тричлен у вигляді квадрата двочлена: 633. а) p 2 + 2 pq + q 2; б) c 2 - 2 c + 1; в) b 2 + 4 b + 4; г) x 2 - 6 x + 9; д) 36 + 12 b + b 2; е) 25 + z 2 - 10 z. 634. а) 4 a 2 - 4 a + 1; б) 16 x 2 + 8 x + 1; в) 1 - 14 b + 49 b 2; г) 4 x 2 + 12 x + 9; д) 25 b 2 - 20 b + 4; е) -40 b + 16 + 25 b 2. 635. а) 4 x 2 + 4 xz + z 2; б) m 2 - 6 mn + 9 n 2; в) 16 a 2 - 8 ab + b 2; г) 4 c 2 + 12 ca + 9 a 2; д) 49 x 2 - 28 xy + 4 y 2; е) 25 p 2 + 9 q 2 - 30 pq. 636. а) x 2 + 4 x + 4; б) a 2 - 10 a + 25; в) 16 - 8 b + b 2; г) 9 k 2 - 6 k + 1; д) 4 b 2 + 16 b + 16; е) 64 - 80 s + 25 s 2; є) 16 a 2 + 8 ab + b 2; ж) 25 m 2 - 20 mn + 4 n 2; з) 9 b 2 + 16 c 2 - 24 bc. Знайдіть значення виразу: 637. а) x 2 - 4 x + 4, якщо x = 12; x = 2,1; x = -18; б) 9 a 2 - 6 a + 1, якщо a = 7; a = -33. 638. 4 a 2 + 4 a + 1, якщо a = 4,5; a = -5,5.
Розкладіть на множники: 639. а) 0,25 m 2 + 2 mn + 4 n 2; б) 0,36 c 2 - 0,6 cx + 0,25 x 2; в) 6,25 х 2 + 1,5 xyz + 0,09 y 2 z 2; г) 196 а 4 x 4 - 2,8 a 2 b 2 x 2 y 4 + 0,01 b 4 y 8; д) х 2 + х + 640. а) 0,01 a 2 + 4 ab + 400 b 2; б) 0,64 x 2 - 0,32 xy + 0,04 y 2; в) 1,44 m 4 n 2 - 1,2 m 2 nk 3 + 0,25 k 6; г) p 2 - Знайдіть значення виразу: 641. а) 4 x 2 + 4 xy + y 2, якщо x = б) а 2 - 3 а + 2,25, якщо a = 11,5; a = -7,5. 642. m 2 - 6 mn + 9 n 2, якщо m = Розв’яжіть рівняння: 643. а) х 2- 8 х + 16 = 0; б) у 2+ 12 у + 36 = 0. 644. а) z 2- 6 z + 9 = 0; б) x 2+ 10 x + 25 = 0.
645. Знайдіть таке число b, для якого даний вираз є квадратом двочлена: а) 64 х 2+ 80 х + b; б) 646. Подайте многочлен у вигляді суми квадратів двох виразів: а) 2 у 2 + 2 y + 1; б) а 4 + 3 а 2 + 1; в) а 2+ b 2 + 2 a + 2 b + 2; г) m 2 + 2 mn + 2 n 2 + 2 n + 1. 647. Подайте многочлен 9 х 2 + 6 ху + 2 у 2 + 4 у + 4 у вигляді суми квадратів двох виразів. Для яких значень х та у значення цього многочлена дорівнює нулю? 648. Розв’яжіть рівняння: (х 2 + 4 х + 4)2 - (х + 2)4 = 0. Вправи для повторення 649. Знайдіть значення виразу: а) (a 2 bc 2)2 × b 2, якщо a = 4; b = -0,3; c = 0,25; б) (5 а 3 b)2 × аb 5, якщо а = 0,2; b = 5. 650. Для яких значень х значення виразу (2 х + 1)2- 4(х 2 + 3 х) дорівнює: 1; -1? 651*. У першій чашці є кава, у другій — стільки ж молока. З першої чашки в другу перелили ложечку кави, потім таку ж ложечку суміші перелили з другої чашки в першу. Чого більше: молока у першій чашці чи кави в другій? 652. Запишіть у вигляді виразу: а) куб суми чисел m і n; б) суму кубів чисел m і n; в) куб різниці чисел а і с; г) різницю кубів чисел а і с. 653. Запишіть у вигляді куба вираз: а) 8 x 3; б) -8 х 3; в) 64 а 9; г) -0,027 а 6 b 12. 654. Запишіть у вигляді многочлена стандартного вигляду: а) (х + 4)(х 2 + 2 х - 3); б) (а - 2 b)(а 2 - 2 аb + 2 b 2).
|
|||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.247 (0.006 с.) |

 Приклади розв’язання вправ
Приклади розв’язання вправ Рівень А
Рівень А 613. а) y 2 - 36 = 0; б) 100 x 2 - 49 = 0.
613. а) y 2 - 36 = 0; б) 100 x 2 - 49 = 0.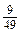 a 2 - 16 x 4 y 8; е)
a 2 - 16 x 4 y 8; е) 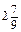 - 0,81 a 4 b 8 c 12.
- 0,81 a 4 b 8 c 12. a 8 b 4 c 2 -
a 8 b 4 c 2 - 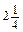 х 6.
х 6.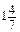 і b =
і b = 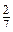 .
.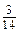 і q =
і q = 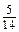 .
. Рівень В
Рівень В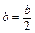 .
. б)
б) 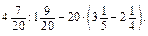
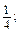 е) a 2 -
е) a 2 - 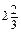 a +
a + 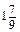 .
.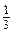 p +
p +  .
.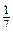 ; y =
; y = 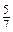 ;
;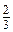 ; n =
; n =