
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі підвищеної складностіСодержание книги
Поиск на нашем сайте
До § 1. Лінійні рівняння з однією змінною 1122. Розв’яжіть рівняння: а) | х - 1| + | x + 1| = 0; б) | х - 4| + |2 x - 8| = 0. 1123. Скільки коренів залежно від числа а (кажуть: параметра а) має рівняння: а) | х - а | = 0; б) | х | = а; в) | х - а | + | x - 1| = 0? 1124. Розв’яжіть рівняння ах = а з параметром а. ● Розв’язання. Розглянемо два випадки. 1) а ≠ 0. Тоді: ах = а; х = 1 (поділили обидві частини рівняння на а). 2) а = 0. Тоді: ах = а; 0 х = 0; коренем рівняння є будь-яке число. Відповідь. Якщо а ≠ 0, то х = 1; якщо а = 0, то коренем рівняння є будь-яке Розв’яжіть рівняння з параметром а: 1125. а) х - а = 3; б) х + а = -4; в) 3 х = а; г) -2 х = а + 2; д) 0,5 х + 3 а = 1,5; е) а - 4 х = 3 а. 1126. а) ах = 5; б) ах = 0; в) ах = 10 а; г) (а + 2) х = 2; д) 4 ах + 4 а = 8 а; е) а (1 - х) = 5 а. 1127. Дано рівняння а (х - 1) + 5 а = 8(х + а) + 1 з параметром а. а) Для яких значень а рівняння не має коренів? б) Чи існують значення а, для яких рівняння має більше, ніж один 1128. З міста А до міста В виїхав автобус і рухався зі швидкістю 60 км/год. Через півгодини він зустрів легковий автомобіль, який їхав з міста В. Цей автомобіль доїхав до міста А і через 40 хв виїхав назад до міста В. За 20 км від міста В легковий автомобіль наздогнав автобус. Знайдіть відстань між містами, якщо швидкість легкового автомобіля весь час становила 90 км/год. 1129. Сплав міді, цинку й олова, загальна маса якого дорівнює 1 кг, містить олова на 20% більше, ніж міді, а цинку ¾ на 50% більше, ніж олова. Знайдіть масу цинку в сплаві. 1130. Оля любить каву з молоком. Коли їй дали повну чашку самої кави, вона відпила 1131. Велосипедист проїхав деякий шлях зі сталою швидкістю. Якби він їхав на 2 км/год швидше, то затратив би на цей шлях в 1,1 менше часу. З якою швидкістю їхав велосипедист? До § 2. Цілі вирази 1132. Чи можна в запису * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 поставити замість зірочок знаки «+» або «–» так, щоб значення одержаного числового виразу дорівнювало: а) 5; б) 0; в) 60? 1133. Доведіть, що для будь-якого натурального значення n значення виразу n (n + 1) + (n + 2)(n + 3) є складеним числом. 1134. Вираз а 2 + 2 аb + 2 a - b + 4 для a = 2 і деякого значення b набуває значення 0. Якого значення набуває вираз а 2 + аb + b 2 для тих самих значеннях a і b? 1135. Для деяких натуральних значень m і n число 3 m + 2 n ділиться на 7. Доведіть, що для тих самих значень m і n на 7 ділиться й число: а) 10 m + 9 n; б) 4 m + 5 n; в) m + 3 n. 1136. Для деяких натуральних значень m і n число 5 m - n ділиться на 8. Для тих самих значень m і n на 8 ділиться і число 3 m + 4 n. Доведіть, що тоді й самі числа m і n діляться на 8. 1137. а) Доведіть, що коли два цілі числа при діленні на 7 дають рівні остачі, то різниця цих чисел ділиться на 7. б) Доведіть, що серед будь-яких восьми цілих чисел завжди знайдуться два числа, різниця яких ділиться на 7. 1138. Запишіть формулу цілих чисел, які діляться на 5, а при діленні на 2, 3 і 4 дають в остачі 1. 1139. (Задача - жарт.) Жінка несла на базар 2 кошики яєць. Її ненароком штовхнув чоловік, кошики впали, а яйця розбилися. Чоловік, щоб розрахуватися, запитав, скільки було всього яєць. Жінка відповіла: ¾ Я їх не рахувала, але коли складала в кошики по 2, по 3, по 4, по 5, по 6, то щоразу залишалося по одному яйцю, а коли складала по 7, то залишилось 2 яйця. Ще знаю, що в кожний кошик поміщається не більше 70 яєць. Скільки яєць було в кошиках? 1140. До деякого трицифрового числа праворуч дописали одну цифру і від одержаного числа відняли початкове. Виявилося, що різниця ділиться на 9. Яку цифру дописали? 1141. Доведіть, що число 1142. а) Доведіть, що сума чисел б) Доведіть, що не існує трицифрового числа 1143. Два учні по черзі пишуть n -цифрове число: число одиниць пише перший, число десятків — другий, число сотень — знову перший і т. д. Чи може другий учень досягти того, щоб одержане число ділилося на 9, якщо перший заважає йому це зробити? Розгляньте випадки: а) n = 10; б) n = 15. До § 3. Одночлени 1144. Доведіть, що для кожного натурального значення n число: а) 34 n + 4 ділиться на 5; б) 92 n - 1 ділиться на 10. 1145. Доведіть, що для кожного натурального значення n число 42 n + 4 ділиться на 10. 1146. Доведіть, що для кожного натурального значення n число 10 n – 4 ділиться на 3, але не ділиться на 9. 1147. Доведіть, що не існує натуральних чисел m і n, для яких була б правильною рівність m (m + 1) = 3 n + 2 n. 1148. Що більше: а) 125125 чи 25185; б) 2508 чи 3757? 1149. Якою цифрою може закінчуватися запис квадрата цілого числа; четвертого степеня цілого числа; восьмого степеня цілого числа? 1150. а) Доведіть, що не існує цілого числа, квадрат якого дорівнює б) Чи існують натуральні значення m і n, для яких рівність m 4 = 10 n + 4 є правильною? в) Доведіть, що не існує натуральних чисел m і n, для яких була б правильною рівність m 8 = 10 n + 2. 1151. Знайдіть найменше натуральне число, яке внаслідок множення на 2 дає квадрат натурального числа, а внаслідок множення на 3 — куб натурального числа. До § 4. Многочлени 1152. а) Число n при діленні на 6 дає в остачі 3, а число m ¾ в остачі 4. Яку остачу при діленні на 6 дає число: 3 n + 5 m; nm? б) Числа m, n і k при діленні на 5 дають відповідно в остачах 2, 3 і 4. Доведіть, що число nk - m (m - 1) ділиться на 5. 1153. У чотирицифровому числі число десятків і число тисяч на 1 більші від 1154. Двоцифрове число в сумі з числом, записаним тими ж цифрами, але у зворотному порядку, дає квадрат натурального числа. Знайдіть усі двоцифрові числа, які мають таку властивість. 1155. Розв’яжіть рівняння (5| x | - 6)(3| x | + 5) = 5(3 x 2 + 1). 1156. Розв’яжіть рівняння з параметром: а) 2(x – 3) = 3(x – a); б) 4(| x | – 1) = a – 4. 1157. Доведіть, що для будь-якого значення параметра а коренем рівняння х (x + а 2) - а 2 = x (x - 1) + 2 є додатне число. 1158. Доведіть, що: а) 1 + 2 + 22 + 23 + … + 29 + 210 = 211 - 1; б) 4(1 + 5 + 52 + 53 + … + 58 + 59) = 510 - 1. Вказівка. а) 1 + 2 + 22 + 23 + … + 29 + 210 = (2 – 1)(1 + 2 + 22 + 23 + … + 29 + 210). Виконавши множення, спростіть останній вираз. 1159. Доведіть, що значення виразу277 + 911 - 815 ділиться на 11. 1160. Доведіть, що значення виразу 1161. Доведіть, що сума чотирьох послідовних натуральних степенів числа 3 ділиться на 120. Розкладіть на множники: 1162. a) 2 a - a 2 - 6 b + 9 b 2; б) 81 x 2 - 49 x 2 y 2 + 144 xy + 64 y 2; в) a 2 b + ab 2 + b 2 c + bc 2 + c 2 a + ca 2 + 3 abc. До § 5. Формули скороченого множення 1163. Спростіть вираз(a - (- b) n)2 + (a + (- b) n)2, де n ¾ натуральне число. 1164. Розв’яжіть рівняння: а) (| x | - х)(| x | + х) = 1- | x |; б) (2| x | - 1)(2| x | + 1) = (x - 1)(4 x - 1); в) (1 - | x |)(1 + | x |)(1 + | x |2) + x 4 = | x |. Розкладіть на множники: 1165. а) (a 2 + 1)2 + 6(a 2+ 1)+ 5; б) (с 2 - 3 с)2 - 2(с 2- 3 с)- 8; в) (а 2 - 4 a)2 - 2 a 2 + 8 a - 15; г) (x 2 + 2 x)2 - 2(x 2 + 2 x)- 3. 1166. а) a 4+ 4 а 2 - 5; б) a 4 + а 2 + 1. 1167. а) а 2+ b 2 + c 2 + 2 ab + 2 bc + 2 ca; б) 4 х 2 + 4 ху + у 2 + 4 х + 2 у + 1. 1168. Доведіть, що значення виразу 256 - 221 ділиться на 497. 1169. Доведіть, що різниця четвертих степенів двох цілих чисел, одне з яких при діленні на 5 дає в остачі 1, а друге ¾ в остачі 2, кратна 5. 1170. Різниця квадратів натуральних чисел m і n є простим числом. Доведіть, що: а) m = n + 1; б) число 4 m + n 2є квадратом цілого числа. 1171. Знайдіть усі натуральні числа m і n, для яких є правильною рівність: а) (m + n)2- n 2 = 3; б) m 2- (m - n)2 = 9. 1172. Знайдіть усі цілі значення m і n, для яких виконується рівність (n + 2 m)2- (n + m)2 = 5. 1173. Доведіть, що не існує натуральних чисел m і n, для яких була б правильною рівність: а) m 3- (m - 2 n)3 = 99; б) (2 m + 1)3+ (m + 2)3 = 2 n. 1174. Доведіть, що коли число y є середнім арифметичним чисел x і z, то x 4 + 2 x 3 z – 2 xz 3 – z 4 – 4 x 2 y 2 + 4 y 2 z 2 = 0. Розв’яжіть рівняння: 1175. а) 1176. а) 1177. а) х 3 – 7 х – 6 = 0; б) х 4 + 2 х 2 – 3 = 0. 1178. а) 1179. Розв’яжіть рівняння з параметром а: а) 1180. Знайдіть найменше значення а, для якого рівняння 1181. а) Доведіть, що квадрат цілого числа або ділиться на 3, або при діленні на 3 дає в остачі 1. Вказівка. Ціле число n може мати вигляд: 1) n = 3 k; 2) n = 3 k + 1; 3) n = 3 k + 2, де k ¾ ціле число. Розгляньте три можливі випадки. б) Доведіть, що для кожного натурального значення п число 3 п + 2 не є квадратом цілого числа. в) Доведіть, що сума квадратів трьох послідовних цілих чисел не є г) Доведіть, що не існує натуральних чисел m і п, для яких виконувалася б рівність m 2 + 1 = 3 п. 1182.а) Доведіть, що не існує цілих чисел m і n, для яких виконувалася б рівність 8 n + 2 = m 2. Вказівка. Припустимо, що такі цілі числа m і n існують. Тоді з рівності 8 n + 2 = m 2 випливає, що m 2 є парним числом. Тому й число m ¾ парне. Нехай m = 2 k, де k ¾ ціле число. Обґрунтуйте, що рівність 8 n + 2 = 4 k 2 для цілих n і k не може бути правильною. б) Доведіть, що серед чисел виду 8 n + 2, де n ¾натуральне число, немає квадрата цілого числа. в) Доведіть, що сума квадратів двох послідовних непарних чисел не є квадратом цілого числа. 1183. а) Нехай n ¾ деяке натуральне число. Доведіть, що за числом n 2 наступні 2 n натуральних чисел не є квадратами натуральних чисел. б) Доведіть, що число 520 + 1 не є квадратом натурального числа. в) Доведіть, що не існує натуральних чисел m і n, для яких виконувалася б рівність 52 m + 4 = n 2. До § 6. Функції
До § 7. Системи лінійних рівнянь із двома змінними 1186. Знайдіть усі значення параметра а, для яких одним з розв’язків рівняння 2(5 а + 1)2 х - 5(2 а - 1)2 у = 7 є пара чисел (2; 5). 1187. Розв’яжіть у цілих числах рівняння: а) 3 n – 7 m = 5; б) n 2 – m 2 = 9; в) n 2 + 2 mn – 8 m 2 = 7; г) n 2 + 2 m 2 – 2 mn – 4 m + 4 = 0. 1188. Побудуйте графік рівняння: | х | - | y | = 0. Розв’яжіть систему рівнянь: 1189. а) 1190. а) 1191. а) Примітка. Рівняння систем містять 3 змінні: х, у і z. Розв’язати такі системи означає знайти всі значення змінних х, у і z, для яких кожне рівняння системи перетворюється у правильну числову рівність. 1192. Скільки розв’язків має система рівнянь 1193. Для яких значень а система рівнянь 1194. Дано 10 чисел. Відомо, що сума будь-яких дев’яти із цих чисел дорівнює 1. Чому дорівнює сума усіх даних чисел? 1195. Двома паралельними залізничними коліями рухаються назустріч один одному два поїзди. Довжина першого поїзда дорівнює 130 м, а другого ¾ 104 м. Зустрівшись, поїзди протягом 4,68 с йшли один повз другий. Якби поїзди рухалися в одному напрямі й перший поїзд переганяв другий, то вони йшли б один повз другий протягом 46,8 с. Знайдіть швидкість кожного поїзда. Логічні задачі 1196. До вершини гори ведуть сходи, що мають 1001 сходинку. На найнижчих 500 сходинках лежать камені — по одному на сходинці. Сізіф може взяти довільний камінь і перенести його вгору, але не далі як на найближчу вільну сходинку. Після цього Аїд може скотити вниз на одну сходинку довільний камінь, якщо попередня сходинка є вільною. Сізіф та Аїд діють по черзі. Починає Сізіф, і його мета — покласти камінь на верхню сходинку. Чи може Аїд цьому завадити? 1197. На дошці написані числа 1, 2, 3, …, 21. Дозволяється стерти будь-які два числа і написати їх різницю (якщо стерли числа а і b, то можна написати число а – b або число b - а). Повторивши цю операцію 20 разів, одержимо одне число. Чи може це число дорівнювати: а) 1; б) 0? 1198. Книга має 320 сторінок. Чи можна вибрати деяких 15 аркушів цієї книги так, щоб сума номерів вибраних 30 сторінок дорівнювала 1500? 1199. П’ять рибалок наловили 9 рибин. Доведіть, що принаймні двоє з них наловили рибин порівну. 1200. Двоє з чотирьох друзів завжди кажуть правду, а двоє — завжди брешуть. Одного разу відбулася така розмова. Другий до першого: «Ти брехун». Третій до другого: «Сам ти брехун». Четвертий до третього: «Обидва вони брехуни, як і ти, до речі». Хто з них каже правду? 1201. Чи можна з 82 куль, кожна з яких має певний колір, вибрати 10 куль так, щоб усі вони мали різні кольори або деякий один колір? 1202. В абетці мови острова Абаба є лише дві букви а і б. Ім’я будь-якого жителя острова можна одержати, замінюючи у слові Абаба записані підряд букви аб на ббб, ба — на ааб, чи бб — на ааа (заміну можна робити кілька разів). Чи є на острові житель з ім’ям Бааабба? ВІТЧИЗНЯНІ МАТЕМАТИКИ
Народився Феофан Прокопович у Києві 7 червня 1681 року в родині крамаря. Він рано втратив батьків, і його опікуном став дядько по матері, виборний ректор Києво-Могилянської академії Феофан Прокопович (Перший). Дядько віддав свого семирічного небожа до початкової школи при Прагнучи поглибити свої знання, сімнадцятирічний Феофан Прокопович вирушив у традиційну для того часу освітню мандрівку. Два роки перебував у Львові, читав студентам лекції з поетики та риторики. Відтак вирушив до Рима, де став учнем колегіуму св. Афанасія. У 1702 році Феофан Прокопович повертається пішки в Україну. З 1704 року він працює в Києво-Могилянській академії, де викладає філософію. Його улюбленим предметом була математика. Тож не дивно, що у курс філософії він включив два математичні курси — арифметику й геометрію, створивши оригінальні підручники із цих предметів. У 1707 році Феофана Прокоповича обирають префектом (заступником ректора), з 1711 до 1715 року він був ректором Києво-Могилянської академії. У 1715 році за викликом царя Феофан Прокопович мусив вирушити до Петербурга, де брав участь у створенні Петербурзького університету та Російської академії наук. У 1721 його призначають віце-президентом найсвятішого синоду. Найзначнішою математичною роботою Феофана Прокоповича є курс лекцій з математики «Арифметика і геометрія, два перші й найбільш плодовиті початки математичних наук, пояснені у Києво-Могилянській академії…», теоретичні відомості в якому на той час були найповнішими в царській Росії.
Михайло Остроградський народився 1801 року на Полтавщині в сім’ї поміщика. Вже в дитячому віці він проявляв дивовижну допитливість та спостережливість, проте вчився в Полтавській гімназії, куди його віддали у дев’ять років, посередньо з усіх предметів. Михайло мріяв про військову кар’єру й дуже зрадів, коли батько вирішив забрати його з гімназії і влаштувати в один із гвардійських полків. В останній момент за порадою одного з родичів, який помітив неабиякі здібності хлопця, було вирішено продовжити навчання. У шістнадцять років Остроградський став студентом Харківського університету. У 1818 році Остроградський склав іспити за повний курс університету, а в 1820 році склав іспити на звання кандидата наук. Проте університетська влада, вважаючи Остроградського «неблагонадійним», відмовилася присуджувати йому вчений ступінь і навіть позбавила диплома про закінчення університету. І все ж Остроградський став відомим ученим, академіком. Невдача лише розпалила в ньому бажання наполегливо працювати. Він їде до Парижа і там відвідує лекції Коші, Лапласа, Пуассона та інших визначних математиків. Спілкування з французькими вченими, вивчення їхніх праць приводить згодом Остроградського до власних відкриттів. Його роботи публікуються в журналі Паризької Академії наук. Чутки про неабиякі успіхи Остроградського дійшли до Батьківщини. У 1828 році Остроградський повернувся у царську Росію. У Петербурзі він викладав математику в Головному педагогічному інституті, Морському кадетському корпусі та в Михайлівському артилерійському училищі. Михайло Остроградський написав багато математичних праць, серед яких є праці з алгебри та теорії чисел, він є автором кількох підручників, а теореми, формули Остроградського вивчають студенти математичних спеціальностей усіх університетів світу.
У 1897 році Дмитро Граве захистив докторську дисертацію і переїхав до України. Спочатку він працював професором Харківського університету та Харківського технологічного інституту. 1902 року професор Граве очолив кафедру чистої математики Київського університету, де тривала вся його подальша науково-педагогічна діяльність. У 1905–1915 роках Дмитро Граве розробив кілька навчальних курсів, які належать здебільшого до алгебри та теорії чисел, найвагомішими з яких є «Елементарний курс теорії чисел» й «Елементи вищої алгебри». Він розвинув на математичному відділенні Київського університету семінарську форму занять зі студентами. Наприкінці 1933 року був організований Інститут математики Академії наук УРСР, першим директором якого став Граве. Неабиякою заслугою Дмитра Граве було створення першої в Україні всесвітньо визнаної алгебраїчної школи.
Михайло Кравчук народився 30 вересня 1892 року в селі Човниці (тепер Ківерцівський район Волинської області) в сім’ї землеміра. У 1910 році золотий медаліст Луцької гімназії стає студентом фізико-математичного факультету Київського університету ім. св. Володимира. У 1915–1917 роках Кравчук виїздить до Москви на спеціальні студії, де складає магістерські іспити. 1918 року його обирають приват-доцентом Київського університету. У 1924 році Михайло Кравчук захищає докторську дисертацію. Протягом 1927–1938 років працює у вищих навчальних закладах Києва. З часу створення у Києві Інституту математики (1933 р.) і до початку 1938 року очолює у ньому відділ математичної статистики. Михайло Кравчук був організатором першої в Україні математичної олімпіади школярів (1935 р.). У вересні 1938 року Кравчука заарештовано сталінським режимом, його звинувачено в українському буржуазному націоналізмі. Вирок — тюремне ув’язнення терміном на 20 років. Далі — Магадан, де у березні 1942 року Кравчук і помер.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 907; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

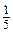 чашки і долила молоком. Потім знову відпила
чашки і долила молоком. Потім знову відпила  ділиться на 37.
ділиться на 37. ,
,  і
і  кратна 111.
кратна 111. .
. ділиться на 7 для будь-якого натурального значення n.
ділиться на 7 для будь-якого натурального значення n. ; б) 1 - x + x 2+ (x 3 - x 2)20 = x.
; б) 1 - x + x 2+ (x 3 - x 2)20 = x. ; б) | х |2 + 2| х | = 3.
; б) | х |2 + 2| х | = 3.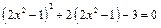 ; б) (х 2 + 4 х)2 – 4 х (х 2 + 4 х) + 3 х 2 = 0.
; б) (х 2 + 4 х)2 – 4 х (х 2 + 4 х) + 3 х 2 = 0. ; б) ах - 2 х = 2 а – 4.
; б) ах - 2 х = 2 а – 4. має хоча б один корінь.
має хоча б один корінь. Рис. 48
Рис. 48
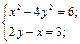 б)
б) 
 б)
б) 
 б)
б) 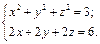
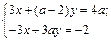 залежно від значень параметра а?
залежно від значень параметра а? має два розв’язки?
має два розв’язки? Феофан Прокопович (1681–1736)
Феофан Прокопович (1681–1736)
 Михайло Васильович Остроградський (1801–1861)
Михайло Васильович Остроградський (1801–1861)
 Дмитро Олександрович Граве (1863–1939)
Дмитро Олександрович Граве (1863–1939)
 Михайло Пилипович Кравчук (1892–1942)
Михайло Пилипович Кравчук (1892–1942)



