
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Різниця і сума кубів двох виразівСодержание книги
Поиск на нашем сайте
Різницю квадратів двох виразів можна розкласти на множники за формулою різниці квадратів. Розкладаючи на множники різницю кубів двох виразів, використовують формулу різниці кубів: a 3 - b 3 = (a - b)(a 2 + ab + b 2). Доведемо цю тотожність, перемноживши вирази a - b і a 2+ ab + b 2: (a - b)(a 2+ ab + b 2) = a 3 + а 2 b + ab 2 - a 2 b - ab 2 - b 3= a 3 - b 3. У формулі різниці кубів тричлен a 2+ ab + b 2 називають неповним квадратом суми виразів а і b (він нагадує тричлен a 2+ 2 ab + b 2, який є квадратом суми виразів а і b). Отже, формулу різниці кубів можна сформулювати так:
При розкладі на множники суми кубів двох виразів використовують формулу суми кубів: a 3 + b 3 = (a + b)(a 2 - ab + b 2). Доведемо цю тотожність: (a + b)(a 2- ab + b 2) = a 3 - а 2 b + ab 2 + a 2 b - ab 2 + b 3= a 3 + b 3. Тричлен a 2- ab + b 2 називають неповним квадратом різниці виразів а і b. Отже,
Приклад 1. Розкласти на множники: а) a 3 - 64; б) 27 a 3+ 125 b 3; в) - x 3- y 6. ● а) a 3 - 64 = a 3 - 43 = (a - 4)(a 2 + 4 a + 16); б) 27 a 3+ 125 b 3 = (3 a)3 + (5 b)3 = (3 a + 5 b)(9 a 2 - 15 ab + 25 b 2); в) - x 3- y 6 = -(x 3 + (y 2)3) = -(x + y 2)(x 2 - xy 2 + y 4). ● Усно 655. Назвіть неповний квадрат різниці виразів: a) x і y; б) c і d; в) p і 1; г) 2 і c. 656. Назвіть неповний квадрат суми виразів:
557. Розкладіть на множники: a) x 3 - y 3; б) m 3 + n 3. Рівень А Розкладіть на множники: 658. a) p 3 - q 3; б) b 3 - 1; в) x 3 - 27; г) 64 - y 3; д) b 3 + c 3; е) a 3 + 8; є) 1 + y 3; ж) 125 + b 3. 659. a) m 3 - n 3; б) b 3 - 8; в) 27 - a 3; г) 1 - z 3; д) x 3 + y 3; е) k 3 + 64; є) p 3 + 1; ж) 27 + c 3. 660. a) 27 x 3 - 1; б) 1 + 64 b 3; в) 8 а 3 - 27; г) 125 - 27 y 3; д) 64 m 3 - 27; е) b 3 + 661. a) m 6 - n 3; б) a 9 + b 6; в) а 6 + c 6; г) x 12 - y 9. 662. a) 8 z 3 + 1; б) 1 - 125 p 3; в) 27 x 3 + 64; г) 125 c 3 - 8; д)
663. Запишіть у вигляді добутку: a) - a 3 + 8; б) - b 3 - c 3; в) -27 + y 3; г) -64 - z 3. Розкладіть на множники: 664. а) 64 a 3 - 27 b 3; б) г) 0,001 a 6 - b 3 c 3; д) 8 x 9 + 125 y 6; е) 1000 - a 3 b 9 c 12. 665. а) 216 b 3 - 27 c 3; б) 125 m 3 + Доведіть, що значення виразу ділиться на дане число: 666. а) 9213 - 8213 на 100; б) 573 + 283 на 85. 667. а) 273 + 373 на 64; б) 753 - 463 на 29. Спростіть вираз: 668. а) (a - b)(a 2+ ab + b 2) + b 3; б) (x 2 - 1)(x 4+ x 2 + 1)+ 1; в) (a 2 + b 2)(a 4- a 2 b 2 + b 4)- а 6 - b 6; г) (a + 2)(a 2- 2 a + 4)- (a - 2)(a 2+ 2 a + 4). 669. а) (x + 3)(x 2- 3 x + 9)- 27;
б) (b - 1)(b 2+ b + 1)+ (b + 1)(b 2- b + 1). Розв’яжіть рівняння: 670. а) (x - 2)(x 2+ 2 x + 4) = x 3+ 4 x; б) (y 2 - 3 y + 9)(y + 3) = 6 y + y 3. 671. а) (1 - x)(1+ x + x 2) = x - x 3; б) -8 z + z 3 = (z - 4)(z 2 + 4 z + 16).
672. Доведіть тотожність: а) (a + b)(a 2 - ab + b 2+ 3 a - 3 b + 3) = (a + 1)3+ (b - 1)3; б) a 4- b 4 = (a - b)(a 3 + a 2 b + ab 2 + b 3); в) a 5- b 5 = (a - b)(a 4 + a 3 b + a 2 b 2 + ab 3 + b 4); г) a 5+ b 5 = (a + b)(a 4 - a 3 b + a 2 b 2 - ab 3 + b 4). Доведіть, що значення виразу ділиться на дане число: 673. а) 1245 - 745 на 50; б) 875 + 885 на 175. Вказівка. Використайте тотожності в) і г) задачі 670. 674. а) 610 + 810 на 100; б) 315 - 220 на 11. 675. Сума і добуток двох чисел відповідно дорівнюють 3,5 і 3. Знайдіть суму кубів цих чисел. Вправи для повторення 676. Спростіть вираз: а) (2 x - y)(x - 2 y)+ 5 xy; б) (3 a - b)(- a + 3 b)+ 3(a 2 + b 2); в) (a 2- a + 1)(a 2+ a + 1) - (а 2+ 1)2. 677. Обчисліть: а) 410 - (45 + 3)(45 - 3); б) 212 × 312 - 4 - (66 + 4)(66- 4). 678. Поїзд затримали на станції А на 10 хв, однак він надолужив згаяний час на перегоні між станціями А і В, пройшовши його зі швидкістю 105 км/год, замість запланованої швидкості 90 км/год. Знайдіть відстань між станціями А і В. 679*. Розв’яжіть рівняння: а) |2 х + 5| = |3 х - 2|; б) | х (х + 1)| = |2 х |. 21. Застосування кількох способів Часто, розкладаючи многочлен на множники, потрібно використати Розглянемо кілька прикладів. 1. Розкладемо на множники многочлен 7 a 2 b 2 - 7 b 4. 7 a 2 b 2 - 7 b 4 = 7 b 2(a 2 - b 2) = 7 b 2(a - b)(a + b). Спочатку винесли спільний множник 7 b 2 за дужки, а потім застосували формулу різниці квадратів. 2. Розкладемо на множники многочлен 6 aс - 9 с - 24 abc + 36 bc. Усі члени многочлена мають спільний множник 3 с. Винесемо його за дужки: 6 aс - 9 с - 24 abc + 36 bc = 3 с (2 a - 3- 8 ab + 12 b). Многочлен 2 a - 3- 8 ab + 12 b розкладемо на множники способом групування: 2 a - 3- 8 ab + 12 b = (2 a - 3)- 4 b (2 a - 3)= (2 a - 3)(1 - 4 b). Отже, 6 aс - 9 с - 24 abc + 36 bc = 3 с (2 a - 3)(1 - 4 b).
Приклад 1. Розкласти на множники тричлен: а) х 2- 6 х - 16; б) а 2+ 2 аb - 8 b 2. ● а) Якщо до виразу х 2- 6 х = х 2- 2×3× х додати 32, тобто 9, то одержимо вираз х 2- 6 х + 9, який є квадратом двочлена х - 3. Тому, виділивши квадрат цього двочлена, матимемо: х 2- 6 х - 16 = х 2- 6 х + 9 - 9 - 16=(х - 3)2- 25 = (х - 3)2- 52 = = (х - 3 - 5)(х - 3+ 5)= (х - 8)(х + 2); б) a 2 + 2 ab - 8 b 2 = a 2 + 2 ab + b 2 - b 2 - 8 b 2 = (a + b)2 - 9 b 2 = = (a + b - 3 b)(a + b + 3 b) =(a - 2 b)(a + 4 b). ●
Приклад 2. Розкласти на множники многочлен m 2 - 4 n 2 - mk - 2 nk. ● m 2 - 4 n 2 - mk - 2 nk = m 2 - (2 n)2 - (mk + 2 nk) = = (m - 2 n)(m + 2 n) - k (m + 2 n) = (m + 2 n)(m – 2 n - k). ● Приклад 3. Розв’язати рівняння 18 x 3- 2 х = 0. ● Розкладемо ліву частину рівняння на множники: 18 x 3- 2 х = 2 х (9 х 2 - 1) = 2 х (3 х - 1)(3 х + 1). Маємо рівняння 2 х (3 х - 1)(3 х + 1) = 0, звідки: х = 0, або 3 х - 1 = 0, або 3 х + 1 = 0; х = 0, або х = Відповідь. 0;
Розкладіть на множники: 680. a) 7 a 2 - 7 b 2; б) km 2 - kn 2; в) 9 x 2 - 36; 681. a) 5 p 2 - 5 q 2; б) 3 b 2 - 27; в) 24 - 6 a 2; г) 3 y 4 - 3 y 2; д) 18 xy 2 - 2 x; е) 4 k 3 + 32; є) 6 a - 6 ab 3; ж) a 3 - a 5. 682. а) 3 p 2 + 6 pq + 3 q 2; б) - b 2+ 2 bc - c 2; в) 81 - 54 b + 9 b 2; г) 2 xb 2 + 8 xb + 8 x; д) 9 a 3 + 6 a 2 + a; е) m - 10 m 2 + 25 m 3. 683. а) 4 x 2 + 8 x + 4; б) n - 14 nc + 49 nc 2; в) -6 a 2 + 24 ab - 24 b 2; г) x 3 - 12 x 2 + 36 х. Знайдіть значення виразу: 684. а) 4 x 2 - 4 у 2, якщо x = 51; у = 49; б) 5 a 2 - 10 ab + 5 b 2, якщо a = 7,3; b = 2,3. 685. а) 3 m 2 + 6 mn + 3 n 2, якщо m = 4,8; n = 5,2; б) 10 a 2 - 10 b 2, якщо a = 63; b = 37. Розв’яжіть рівняння: 686. а) 8 x 2- 72 = 0; б) 12 x 2 - 3 = 0. 687. а) 5 x 2- 125 = 0; б) 50 x 2 - 2 = 0.
Розкладіть на множники: 688. a) a 4 - n 4; б) k 4 - 16. 689. a) x 4 - 1; б) 81 - b 4. 690. а) 3 mn + 24 n - 9 m - 72; б) bx 4 - x 4 + bx 3 - x 3; в) -4 abc - 32 bc - 12 ac - 96 c; г) 2 y 4 - 2 y 3 a + 2 y 2 ab - 2 y 3 b; д) 1,5 a 2- 0,5 a 2 x + 1,5 ax - 0,5 ax 2; е) x 2 y 2 a - x 2 y 2 + 5 axy - 5 xy. 691. a) 4 ac + 2 bc + 4 xac + 2 xbc; б) m 2 a - m 2 b + 3 am - 3 bm; в) - a 3 b - a 2 b 2 - a 2 b - ab 2; г) 0,2 x 4 + 0,6 x 3 y - 0,4 x 3 - 1,2 x 2 y. 692. а) x 2 - 2 xy + y 2- z 2; б) в) c 2 + 9- 6 c - k 2; г) 4 x 2 - 4 y - y 2 - 4. 693. а) m 2 + 2 mn + n 2- k 2; б) в) a 2 - 8 a - b 2 + 16; г) p 2 - 25 + 10 q - q 2. 694. Розкладіть многочлен a 2 + 2 ab + b 2- c 2 + 2 c - 1 на множники. Доведіть, що коли a + b + с = 1, то значення цього многочлена дорівнює нулю. 695.Розкладіть на множники многочлен a 2 + 2 a + 1 - b 2- c 2 + 2 bc та знайдіть його значення, якщо a = -1 і b = с. Розкладіть на множники: 696. а) a 2 - b 2 + a + b; б) x 2 - a 2 + x - a; в) 4 x 2 + y - 2 x - y 2; г) 3,5 x 2 - 3,5 y 2 - x + y. 697. а) c 2 - b 2 + c - b; б) x + y + x 2 - y 2 ; в) a 2 + 4,8 ab - x 2 - 4,8 xb. Розкладіть на множники та знайдіть значення виразу: 698. а) x 2 - y 2+ (x + y)2, якщо х = б) a 2 + (a + 4)2 - 16, якщо а = 96. 699. а) a 2 - b 2+ (a - b)2, якщо а = б) (m - 2)2+ m 2 - 4, якщо m = 102. Розв’яжіть рівняння: 700. а) x 3- x = 0; б) 1,6 y 3 - 0,4 y = 0; в) x 3 - 4 x 2 - 4 x + 16 = 0; г) 2 z 3 - z 2 = 8 z - 4; д) x 4 - x 3 - x 2 + x = 0; е) x 3 - 2 x 2 + 4 x - 8 = 0. 701. а) x 3- 4 x = 0; б) 1,2 z 3 - 0,3 z = 0; в) x 3 - x 2 - 9 x + 9 = 0; г) 4 y 3 - y 2 = 4 y – 1.
Розкладіть на множники: 702. а) х 2+ 2 х - 8; б) а 2- 8 а + 12; в) 4 с 2- 4 с - 3; г) х 2- 6 ху + 5 y 2; д) а 2+ 12 аb + 11 b 2; е) 9 а 2- 6 аb - 8 b 2. 703. а) 2 a 2+ a - 4 ab - b + 2 b 2; б) a 3 - b 3- (a - b)3. 704. Розв’яжіть рівняння: а) х 2- 8 х + 7 = 0; б) у 2+ 12 у + 20 = 0; в) (x - 1)2- 6(x - 1) + 8 = 0; г) (x - 1)(x - 3)(x 2 - 3) = (x - 1)(x - 3). 705. Доведіть тотожність: a 6- b 6 = (a - b)(a + b)(a 2 - ab + b 2)(a 2 + ab + b 2). 706. Доведіть, що значення виразу 334 + 992 - 330- 990 ділиться на 80. 707. Доведіть, що значення виразу 1110 + 4 × 749 + 1111- 4 × 748 ділиться на 12. 708. Доведіть, що рівність a 3+ b 2 = ab (а + 1) є правильною тільки тоді, коли b = а або b = а 2. Вправи для повторення 709. Подайте у вигляді многочлена: а) (3 a + 2 b)(4 a - b)+ 2 b 2; б) 2 x (y + 15 x) + (x - 6 y)(5 y + 2 x). 710. Розв’яжіть рівняння: а) 711. Запишіть у вигляді виразу: а) подвоєний добуток змінної а та суми змінних m і n; б) різницю квадратів виразів а – 1 і bc. 712. Сплав срібла і міді, загальна маса якого дорівнює 2 кг, містить 80% міді. Знайдіть масу срібла у сплаві. 713. Сплав міді й цинку має масу 4,2 кг. Знайдіть масу міді, якщо її у сплаві на 10% більше, ніж цинку. 714. До сплаву міді й олова, загальна маса якого дорівнює 2 кг, додали 200 г міді й одержали новий сплав, у якому міді стало в 1,2 разу більше, ніж олова. Скільки відсотків міді містив перший сплав?
|
||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.180 (0.008 с.) |

 Приклади розв’язання вправ
Приклади розв’язання вправ a) m і n; б) p і q; в) a і 1; г) 3 і x.
a) m і n; б) p і q; в) a і 1; г) 3 і x.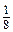 ; є)
; є)  y 3 - 1; ж)
y 3 - 1; ж)  Рівень Б
Рівень Б p 3 - 8 q 3; в) 27 а 6 - 125;
p 3 - 8 q 3; в) 27 а 6 - 125; n 6; в) 0,064 x 9 y 6 z 3 - 27.
n 6; в) 0,064 x 9 y 6 z 3 - 27. Рівень В
Рівень В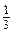 , або х = -
, або х = -  x 2 - a 2 - 2 ab - b 2;
x 2 - a 2 - 2 ab - b 2; а 2 - 4 x 2 - 4 xy - y 2;
а 2 - 4 x 2 - 4 xy - y 2;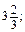 у =
у = 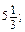
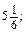 b =
b = 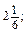
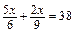 ; б)
; б) 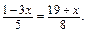
 Для тих, хто хоче знати більше
Для тих, хто хоче знати більше


