
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функція. Способи задання функціїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Функції та способи їх задання. Нехай сторона квадрата дорівнює а см, а його периметр — Р см. Знаючи сторону а, за формулою P = 4 а можна знайти відповідне їй значення периметра P. Наприклад, якщо а =6, то P = 4 · 6 = 24; якщо а = 0,1, то P = 4 · 0,1 = 0,4; якщо а = 2,5, то P = 4 · 2,5 = 10. Бачимо, що значення периметра залежать від того, яких значень ми надавали довжині сторони квадрата. Зауважимо також, що кожному значенню довжини сторони відповідає одне певне значення периметра. Так, значенню а =6 відповідає значення P = 24, значенню а = 0,1 — значення P = 0,4. У даному прикладі маємо дві залежні змінні а і P — довжину сторони квадрата і його периметр. Значення змінної а можна вибрати довільно, а значення змінної Р залежать від вибраних значень а. Тому а називають незалежною змінною, а Р ¾ залежною змінною. Розглянемо ще один приклад залежності між змінними. Водій вирішив простежити за лічильником, яку відстань він проїде за 1 год, 2 год, 3 год, 4 год, 4,5 год, 5 год. Результати спостережень він записав у вигляді таблиці:
У даному прикладі маємо дві залежні змінні: час t і шлях S, пройдений за цей час. Значення шляху залежать від значень часу. Так, часу t = 2 відповідає значення шляху S = 170, часу t = 4,5 — значення шляху S = 335. До того ж, кожному значенню часу відповідає одне певне значення шляху. Тому в даному випадку t є незалежною змінною, а S — залежною змінною. У математиці, як правило, незалежну змінну позначають буквою х, а залежну змінну — буквою у. У розглянутих прикладах кожному значенню незалежної змінної відповідає єдине значення залежної змінної. За таких умов для залежної змінної використовують термін «функція».
Для незалежної змінної теж є спеціальний термін: її називають аргументом. Кажуть: у є функцією від аргументу х. Отже, в розглянутих прикладах: периметр Р квадрата є функцією від довжини його сторони а; тут Р — функція, а — аргумент; шлях S є функцією від часу t; тут S — функція; t — аргумент. Перша функція задана формулою P = 4 а. Друга функція задана таблицею. 2. Область визначення та область значень функції. Усі значення, яких набуває незалежна змінна (аргумент), утворюють область визначення функції; усі значення, яких набуває залежна змінна (функція), утворюють область значень функції. Так, область визначення функції, що задається формулою P = 4 а, утворюють усі значення, яких може набувати змінна а. Оскільки ця змінна визначає довжину сторони квадрата, то а може набувати лише додатних значень. Отже, область визначення цієї функції утворюють усі додатні числа. Область значень функції, що задається формулою P = 4 а, утворюють усі значення, яких може набувати залежна змінна Р. Периметр Р не може дорівнювати від’ємному числу або нулю, однак може дорівнювати будь-якому додатному числу. Наприклад, Р може дорівнювати 2, бо 2 — це периметр квадрата зі стороною 0,5. Отже, область значень цієї функції утворюють усі додатні числа. Область визначення функції, заданої таблицею, утворюють числа Розглянемо функцію, задану формулою y = x 2 + 1, де 0 £ х £ 10. Такий запис означає, що областю визначення функції є всі значення х, які задовольняють нерівності 0 £ х £ 10. Якщо функція задана формулою y = x 2 + 1 і не вказано, яких значень можна надавати аргументу, то вважають, що область визначення функції утворюють усі числа.
Приклад 1. Автомобіль, рухаючись зі швидкістю 80 км / год,проходить за t год шлях S км. Задати формулою функцію S від t. Знайти значення функції, які відповідають значенням аргументу: 2; 2,5; 4. ● Функція задається формулою S = 80 t. Якщо t = 2,то S = 80 · 2 = 160; якщо t = 2,5,то S = 80 · 2,5 = 200; якщо t = 4,то S = 80 · 4 = 320. ● Приклад 2.Починаючи із третьої години, через кожну годину міряли атмосферний тиск і записували дані в таблицю:
Залежність між якими змінними задає ця таблиця? Чи задає таблиця функцію? Який тиск у мм ртутного стовпчика був о 4 год; о 8год? Яка область визначення функції; область значень? ● Таблиця задає залежність між годинами t доби й атмосферним тиском р. Змінна р єфункцією від змінної t, бо кожному значенню t відповідає єдине значення р. Якщо t = 4, то за таблицею знаходимо: р = 748. Отже, о 4 годині атмосферний тиск був 748 мм рт. ст. Аналогічно о 8 годині — 755 мм рт. ст. Область визначення функції утворюють числа 3, 4, 5, 6, 7, 8 і 9, а область значень — числа 746, 748, 751, 752, 755 і 756. ● Приклад 3.Функція задана формулою y = х 2 - 3. Скласти таблицю значень аргументу і відповідних значень функції, надавши аргументу таких значень: -6; -3; -2; 0; 2; 3; 6.
Приклад 4.Для яких значень аргументу значення функції дорівнює -3, якщо функція задана формулою: а) y = 2 x - 5; б) y = х 2 + x - 3; в) y = х 2 + 1? ● а) Щоб знайти значення х, для яких у = -3, розв’яжемо рівняння 2 x - 5 = -3: 2 x = 2; х = 1. Отже, функція набуває значення у = -3, якщо х = 1. б) х 2 + x - 3 = -3; х 2 + x = 0; х (х + 1) = 0; x = 0 або х + 1 = 0; x = 0 або х = –1. Функція набуває значення -3, якщо х = 0 або х = –1. в) х 2 + 1 = -3; х 2 = –4 — рівняння коренів не має. Значення -3 дана Усно 768. Нехай x ¾ довжина сторони квадрата, а S ¾ його площа. Чому S є 769. Функція задана формулою y = 5 x. а) Яка змінна є незалежною, а яка — залежною; яка є аргументом, а яка — функцією? б) Яке значення функції відповідає значенню аргументу х = 2; х = -1? в) Якому значенню аргументу відповідає значення функції у = 5; у = 0? 770. Залежності змінної у від змінної х задані таблицями:
(У таблиці б) числам 1, 3, 9 відповідають їхні дільники.) Яка з таблиць задає функцію? Для функції вкажіть область визначення та область значень. 771. Функція задана таблицею:
а) Чому дорівнює значення функції, якщо х = -2; х = 1; х = 4? б) Для яких значень аргументу значення функції дорівнює -1; 7; 3? в) Яка область визначення функції? г) Яка область значень функції?
772. Одна сторона прямокутника дорівнює 6 см, а суміжна — x см. За якою формулою можна обчислити площу S прямокутника? Чи задає ця формула функцію? 773. Густина сталі дорівнює 780 кг/м3. Запишіть формулу, за якою можна обчислити масу сталевого куба з ребром а м. Яка область визначення функції, що задається цією формулою? Знайдіть значення функції, якщо а = 0,2. 774.Автомобіль рухається зі швидкістю 75 км / год. За час t год він проходить шлях S км. Задайте формулою шлях S як функцію від часу t. Знайдіть значення функції, якщо t = 2,4. 775. Довжина прямокутного паралелепіпеда дорівнює 7,5 см, ширина — 4 см, а висота — x см. Задайте формулою об’єм V як функцію від висоти х. Знайдіть значення функції, якщо х = 2,5. 776. Знайдіть значення функції, заданої формулою y = 2 x 2 – x, якщо х = 2; х = 0; х = –1. 777. Знайдіть значення функції, заданої формулою y = 2 x + 1, якщо х = 5; х = 0,5; х = –2. 778. Функція задана формулою y = 18 - 3 x. Складіть таблицю значень функції для значень аргументу: -3; -2; 0; 1; 6. 779. Функція задана формулою y = 2 x 2 + 1. Складіть таблицю значень функції для значень аргументу: -4; -2; 0; 2; 4. 780. Функція задана формулою y = 4 x - 5. Для яких значень аргументу значення функції дорівнює 0; 3? 781. Функція задана формулою y = -2 x + 3. Для яких значень аргументу значення функції дорівнює 1; 5? 782.Функція задана таблицею:
а) Знайдіть значення функції, якщо х = -2; х = 2. б) Для яких значень х значення функції дорівнює -1; 1? в) Яка область визначення функції? г) Яка область значень функції?
783. Функція задана формулою y = 12 x. Заповніть таблицю:
784. Функція задана формулою y = x + 6. Заповніть таблицю:
785. Велосипедист має подолати шлях від села до автостанції завдовжки 7 км, рухаючись зі швидкістю 10км / год. Нехай S км — шлях, який залишилося проїхати велосипедистові через t год після початку руху. Задайте формулою шлях S як функцію від часу t. Знайдіть значення функції, якщо t = 0,5. Яка область визначення і область значень цієї функції? 786.Натуральне число m при діленні на 4 дає неповну частку n і остачу 1. Задайте формулою m як функцію від n. Знайдіть значення функції, якщо n = 50. Яка область визначення і область значень цієї функції? 787. Функція задана формулою y = х 2 - 4 x + 2. Для яких значень аргументу значення функції дорівнює: а) 2; б) -2? 788. Функція задана формулою y = х 2 + 2 x - 3. Для яких значень аргументу значення функції дорівнює: а) –3; б) -4? 789. Функція задана формулою y = 3 x - 1, де змінна х може набувати значень -6; -3; 0; 3; 6; 9. Задайте цю функцію таблицею.
790. Доведіть, що функція y = х 2 + 6 x + 10 не може набувати від’ємних значень. 791. Знайдіть найменше значення функції y = х 2 - 4 x + 2. 792. Для яких значень аргументу значення функції 793. Функція задана формулою y = x 2 + 2 ах, де а — деяке додатне число. Чи набуває ця функція від’ємного значення? Вправи для повторення 794. З міста A до міста B, відстань між якими дорівнює 40 км, виїхав велосипедист, а через 40 хв назустріч йому з міста B — мотоцикліст. Швидкісь велосипедиста дорівнює 15 км / год, а мотоцикліста — 45 км / год. Через скільки годин після виїзду велосипедиста вони зустрінуться? 795*. Скільки трицифрових чисел можна записати за допомогою цифр 0, 3, 6 і 9, якщо у запису чисел цифри можуть повторюватися? 796. На координатній площині позначте точки A (-4; 0), B (0; 1), C (4; -1) та точку D з абсцисою -3 й ординатою 2. 797. Через точку A (3; 0) проведіть пряму, перпендикулярну до осі х, а через точку В (0; 2) — пряму, перпендикулярну до осі у. Знайдіть координати точки перетину проведених прямих. 798. Знайдіть периметр і площу прямокутника ABCD, якщо А (–1; –1), 24. Графік функції. Функція як математична модель 1. Графік функції. Розглянемо функцію, задану формулою y = 0,5 x 2, де -3 £ x £ 2. Знайдемо значення цієї функції для цілих значень аргументу й занесемо результати в таблицю:
Значення х ми вибрали так, що кожне наступне на 1 більше від попереднього. Тому кажуть, що таблиця значень функції складена з кроком 1. Позначимо на координатній площині точки, абсциси яких дорівнюють вибраним значенням аргументу, а ординати ¾ відповідним значенням функції (рис. 4).
Добираючи інші значення x, що задовольняють нерівності -3 £ x £ 2, й обчислюючи відповідні значення y, отримаємо інші пари значень х та у. Графік функції утворюють точки координатної площини, абсциси яких дорівнюють усім значенням аргументу, а ординати ¾ відповідним значенням функції. 2. Графічний спосіб задання функції. Маючи графік функції, можна знаходити її значення за відомим значенням аргументу і навпаки: знаходити значення аргументу за відомим значенням функції. Розглянемо, наприклад, функцію, графік якої зображений на рисунку 6. (Про таку функцію кажуть, що вона задана графічно.)
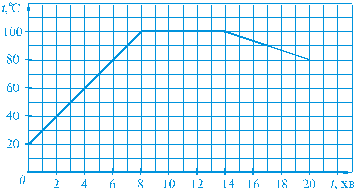
Знайдемо за допомогою графіка значення функції, якщо x = 4. Для цього через точку осі x з абсцисою 4 проведемо пряму, перпендикулярну до осі x. Точка її перетину із графіком функції має координати (4; 8). Отже, якщо x = 4, то значення функції дорівнює 8. Знайдемо за допомогою цього ж графіка значення аргументу, для яких значення функції дорівнює 6. Для цього через точку осі у з ординатою 6 проведемо пряму, перпендикулярну до осі у. Одержимо дві точки її перетину із графіком функції: (2; 6) і (8; 6). Отже, Дивлячись на графік, зображений на рисунку 6, можна відмітити деякі властивості функції, заданої цим графіком. 1) Область визначення функції утворюють усі значення х, що задовольняють нерівності -5 £ x £ 10. 2) Найбільше значення функції дорівнює 9 (цього значення функція набуває, якщо х = 6). 3) Найменше значення функції дорівнює -2 (цього значення функція набуває, якщо х = -5). 4) Область значень функції утворюють усі значення у, що задовольняють нерівності -2 £ у £ 9. 5) Значення функції дорівнює нулю, якщо х = -3. Ті значення аргументу, для яких значення функції дорівнюють нулю, називають нулями функції. Отже, значення х = -3 є нулем даної функції. 6) Функція набуває додатних значень, якщо -3 < x £ 10; від’ємних значень — якщо -5 £ x < –3. 3. Функції як математичні моделі реальних процесів. Розглянемо рисунок 7, на якому зображено графік зміни температури води протягом 20 хв.
Рис. 7 Із графіка видно, що: початкова температура води дорівнювала 20°С; протягом перших 8 хв температура води підвищилась до 100°С, потім протягом 6 хв (від 8 хв до 14 хв) температура води не змінювалась, а протягом наступних 6 хв температура води знизилась до 80°С. Функція, графік якої зображено на рисунку 7, описує реальний процес зміни температури води. Кажуть, що ця функція моделює даний процес, або що вона є математичною моделлю даного процесу. Якщо тіло рухається рівномірно зі швидкістю 15 м/с, то шлях S м, пройдений ним за час t с, можна обчислити за формулою S = 15 t. У цьому випадку функція, задана формулою S = 15 t, є математичною моделлю рівномірного руху. У сьомому та наступних класах ми ознайомимося з багатьма функціями, які можна використати для моделювання реальних процесів та залежностей між різними величинами.
Приклад 1.Побудувати графік функції, заданої формулою: а) y = 0,5 x + 1, де -4 £ x £ 4, склавши таблицю значень функції з кроком 1; б) y = 1 – x 2, де -2 £ x £ 2. ● а) Складемо таблицю значень функції:
Позначимо точки, координати яких подані в таблиці, на координатній площині. Якщо до цих точок прикласти лінійку, то побачимо, що всі вони лежать на одній прямій. Сполучимо відрізком крайні позначені точки. Цей відрізок і є графіком функції y = 0,5 x + 1, де -4 £ x £ 4 (рис. 8).
б) Складемо таблицю значень функції:
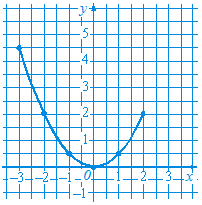
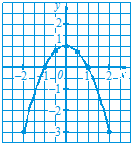
Позначимо точки, координати яких подані в таблиці, на координатній площині. Сполучимо їх плавною лінією. Маємо графік функції, заданої формулою y = 1 – x 2, де -2 £ x £ 2 (рис. 9). ● Приклад 2. Чи належить графіку функції y = 2 x 2 точка А (3; 9); В (2; 8)? ● Точка А (3; 9) належатиме графіку даної функції, якщо значення функції для x = 3 дорівнює 9. Знаходимо: якщо x = 3, то y = 2×32 = 18. Значення функції не дорівнює 9. Отже, точка А (3; 9) графіку функції не належить. Для точки В (2; 8) матимемо: якщо x = 2, то y = 2×22 = 8. Точка В (2; 8) належить графіку функції. ● Приклад 3. На рисунку 10 зображено графік функції. Користуючись графіком, заповнити таблицю:
Рис. 10 ● Заповнимо таблицю:
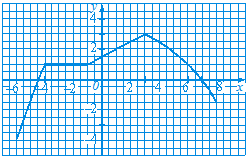
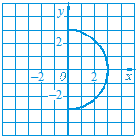
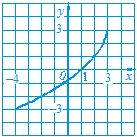
Усно 799. Функція задана графіком (рис. 11). Знайдіть значення функції, якщо х = -2. Якому значенню аргументу відповідає значення функції у = 2? Яка область визначення та область значень функції? 800. Чи є лінія, зображена на рисунку 12, графіком деякої функції? Відповідь обґрунтуйте. 801. Функція задана графіком (рис. 13). а) Знайдіть значення функції, якщо х = -4; х = –2; х = 2. б) Знайдіть значення аргументу, якому відповідає значення функції у = -2; у = 0; у = 3. в) Яка область визначення та область значень функції? г) Чому дорівнюють найбільше та найменше значення функції? д) Вкажіть нулі функції. е) Для яких значень х функція набуває додатних значень; від’ємних значень?
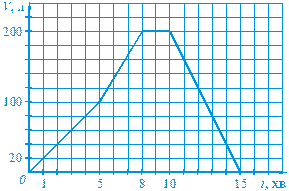
802. На рисунку 14 показано зміну об’єму води в баку залежно від часу.
Рис. 14 а) Скільки води було в баку у початковий момент часу? б) Скільки води поступило в бак протягом перших 5 хв; 8 хв; 10 хв? в) Скільки часу об’єм води в баку не змінювався? г) Протягом скількох хвилин спорожнився бак?
803. На рисунку 15 зображено графік функції. Користуючись цим графіком, заповніть таблицю:
Яка область визначення та область значень функції? Чому дорівнює найменше значення функції?Для яких значень х функція набуває додатних значень? 804. На рисунку 16 зображено графік функції. Користуючись цим графіком, заповніть таблицю:
Яка область визначення та область значень функції?Чому дорівнює найбільше значення функції? Вкажіть нулі функції. Для яких значень х функція набуває від’ємних значень?
805. Побудуйте графік функції, заданої формулою y = 2 x + 1, де -3 £ x £ 3, склавши таблицю значень функції з кроком 1. Чи належать графіку 806.Побудуйте графік функції, заданої формулою y = -3 x - 1, де -2 £ x £ 2, склавши таблицю значень функції з кроком 1. Чи належать графіку функції точки M (0; -1), N (2; 5)? Побудуйте графік функції, заданої формулою: 807. а) y = 808. а) y = 809. На рисунку 17 показано графік залежності висоти польоту літака від часу. а) На якій максимальній висоті летів літак? б) Скільки часу літак набирав висоту?
Рис. 17 Рис. 18
Рівень Б 811. На рисунку 19 зображено графік зміни температури повітря протягом доби.
а) Якою була температура повітря о 2 год; о 9 год; о 18 год; о 24 год? б) О котрій годині температура повітря дорівнювала -2°; 0°; 6°? в) О котрій годині температура повітря була найнижчою; найвищою? 812.На рисунку 20 зображено графік залежності швидкості тіла від часу. а) Яку швидкість мало тіло через 2 с після початку руху; через 5 с; через 10 с; через 20 с? б) У який момент часу швидкість тіла дорівнювала 4 м/с; 6 м/с; 8 м/с? в) У який момент часу швидкість тіла була найменшою? г) Вкажіть час, протягом якого тіло рухалось зі сталою швидкістю. Який шлях пройшло тіло за цей час?
813. На рисунку 21 зображено графік руху групи туристів від табору до автостанції.
814. Графіком функції є ламана ABCD (сукупність трьох відрізків AB, BC і CD), де A (-2; -3), B (0; 3), C (4; 3), D (6; 1). Накресліть графік функції та заповніть таблицю:
Яка область визначення та область значень функції? Вкажіть нулі функції. Для яких значень х функція набуває додатних значень; від’ємних значень? 815.Графіком функції є ламана KLMN, де K (-4; 4), L (-2; 2), M (2; 2), N (3; 3). Накресліть графік функції та заповніть таблицю:
Яка область визначення та область значень функції? Чому дорівнюють найбільше та найменше значення функції? Чи має функція нулі? Для яких значень х функція набуває додатних значень; від’ємних значень? Побудуйте графік функції, заданої формулою: 816. а) y = х (4 - х), де -1 £ x £ 5; б) y = х 2 + 4 х +3, де -3 £ x £ 1. 817. а) y = х 2 - 2 х, де -2 £ x £ 3; б) y = (1 – х)(3 + х), де -2 £ x £ 1.
818. Побудуйте графік функції, заданої формулою: а) б) Вправи для повторення 819. Для яких значень х значення виразу 15 х - 6 дорівнює 3? 820. Розв’яжіть рівняння: а) (2 х + 3)(4 – (2 х + 3)) = 0; б) 821. У першому сплаві є 40% міді, а в другому — 10%. Скільки кілограмів другого сплаву потрібно додати до 10 кг першого, щоб отримати 30-відсотковий сплав міді? 822. Відстань між містами A і B дорівнює 190 км. З міста A до міста B виїжджає автомобіль і рухається зі швидкістю 90 км / год.На якій відстані від міста B він буде через t год? Запишіть розв’язок у вигляді виразу зі змінною. Знайдіть значення цього виразу, якщо t =1,2. Лінійна функція 1. Що таке лінійна функція. Розглянемо кілька прикладів. Нехай тіло рухається рівномірно і прямолінійно зі швидкістю 20 м/с й напрям його руху збігається з напрямом осі х (рис. 22). Якщо в початковий момент руху тіло перебувало на відстані 35 м від початку відліку, то через t с тіло перебуватиме на відстані S = 20 t + 35метрів від нього.
Нехай у басейн через трубу щохвилини вливається 2,5 м3 води. Якщо в початковий момент часу в басейні було 70 м3 води, то об’єм V води (у м3), яка буде у басейні через t хв, можна обчислити за формулою V = 2,5 t + 70. Формулами S = 20 t + 35, V = 2,5 t + 70, де t — незалежна змінна, задаються функції, які називають лінійними.
У формулі y = kx + b змінній х можна надавати будь-яких значень, тому область визначення лінійної функції утворюють усі числа. 2. Графік лінійної функції. Побудуємо графік лінійної функції у = 0,5 х – 1. Для цього складемо таблицю кількох значень х та відповідних значень у:
Позначимо точки, координати яких подані в таблиці, на координатній площині (рис. 23). Приклавши лінійку, переконуємося, що усі позначені точки лежать на одній прямій. Якби для інших значень х обчислили відповідні значення у і позначили б точки з такими координатами на координатній площині, то й вони лежали б на цій прямій. Через позначені точки проведемо пряму. Вона є графіком лінійної функції у = 0,5 х – 1.
Взагалі, графіком лінійної функції є пряма. Щоб побудувати графік лінійної функції, досить знайти координати лише двох точок графіка, позначити ці точки на координатній площині й провести через них пряму. Так, щоб побудувати графік функції у = 0,5 х – 1, досить було взяти дві точки, наприклад, (0; –1) і (2; 0) та провести через них пряму.
Якщо k > 0, то пряма y = kx + b утворює з додатним напрямом осі х гострий кут, якщо k < 0, — тупий кут.
Щоб побудувати графік функції y = 2, досить було позначити на осі у точку з ординатою 2 і провести через неї пряму, паралельну осі х. 4. Властивості лінійної функції y = kx + b. 1) Область визначення функції утворюють усі числа. 2) Якщо k ¹ 0, то область значень функції утворюють усі числа; якщо k = 0, то функція набуває лише одного значення у = b. 3) Графіком функції є пряма. 4) Графік функції утворює з додатним напрямом осі х гострий кут, якщо k > 0, тупий кут, — якщо k < 0. Якщо k = 0, то графік паралельний осі х, зокрема, якщо k = 0 і b = 0, то він збігається з віссю х. 5. Функція у = kx. У формулі y = kx + b, якою задається лінійна функція, покладемо b = 0. Одержимо формулу y = kx, якою задається функція, яка є окремим але досить важливим випадком лінійної функції і служить моделлю багатьох реальних процесів. Розглянемо приклади. 1. Нехай тіло рухається зі швидкістю 20 м/с. Тоді шлях S м, пройдений ним за час t с, можна обчислити за формулою S = 20 t. Ця формула задає шлях S як функцію від часу t. 2. Густина заліза дорівнює 7,8 г/см3. Масу m г заліза, об’єм якого дорівнює V см3, можна обчислити за формулою m = 7,8 V. Ця формула задає масу m як функцію від об’єму V. Перейшовши у прикладах до прийнятих позначень аргументу і функції, матимемо функції, що задаються формулами у = 20 x та у = 7,8 x, тобто формулами виду y = kx, де k ¹ 0. Функцію, яку можна задати формулою виду у = kx, де х — незалежна змінна, k — деяке число, k ¹ 0, називають ще прямою пропорційністю. Оскільки пряма пропорційність є окремим випадком лінійної функції, то графіком прямої пропорційності є пряма. Ця пряма проходить через початок координат (бо якщо х = 0, то у = k × 0 = 0). Для побудови графіка прямої пропорційності досить знайти яку-небудь точку графіка, відмінну від початку координат, і провести через цю точку та початок координат пряму. Побудуємо графік функції На рисунку 27 зображено графіки функцій виду y = kx для різних значень k.
Якщо k > 0, то графік функції y = kx розміщений у першій і третій координатнихчвертях, а якщо k < 0, — у другій і четвертій чвертях.
7. Взаємне розміщення графіків лінійних функцій. Розглянемо дві лінійні функції у = 0,5 х – 2 і у = 0,6 х + 1, формули яких мають різні коефіцієнти біля х. З’ясуємо, чи перетинаються графіки цих функцій (рис. 29). Для цього перевіримо, чи існує значення х, для якого обидві функції набувають одного й того ж значення; іншими словами: чи існує значення х, для якого виконується рівність 0,5 х – 2 = 0,6 х + 1. Розв’яжемо дане рівняння: 0,5 х – 0,6 х = 2 + 1; –0,1 х = 3; х = –30. Якщо х = –30, то обидві функції набувають одного й того ж значення: у = 0,5 × (–30) – 2 = –15 – 2 = –17 і у = 0,6 × (–30) + 1 = –18 + 1 = –17. Отже, графіки функцій перетинаються в точці (–30; –17). Розглянемо дві лінійні функції у = 0,5 х – 2 і у = 0,5 х + 1, формули яких мають однакові коефіцієнти біля х. Рівняння 0,5 х – 2 = 0,5 х + 1 не має коренів. Тому прямі, що є графіками функцій у = 0,5 х – 2 і у = 0,5 х + 1 (рис. 30), не мають спільних точок (ці прямі паралельні).
Взагал
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.51.35 (0.013 с.) |

 Приклади розв’язання вправ
Приклади розв’язання вправ Рівень А
Рівень А Рівень Б
Рівень Б Рівень В
Рівень В дорівнюють нулю?
дорівнюють нулю?





 Рівень А
Рівень А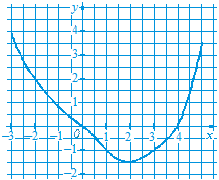

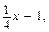 де -4 £ x £ 6; б) y = x 2 – 1, де -2 £ x £ 2.
де -4 £ x £ 6; б) y = x 2 – 1, де -2 £ x £ 2.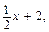 де -6 £ x £ 4; б) y = x 2, де –1 £ x £ 3.
де -6 £ x £ 4; б) y = x 2, де –1 £ x £ 3.
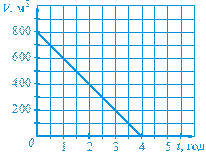
 810.На рисунку 18 показано графік зміни об’єму води в басейні. а) Який процес зображує цей графік: вода поступає в басейн чи витікає з басейну? б) Скільки води було в басейні в початковий момент часу; через 4 год?
810.На рисунку 18 показано графік зміни об’єму води в басейні. а) Який процес зображує цей графік: вода поступає в басейн чи витікає з басейну? б) Скільки води було в басейні в початковий момент часу; через 4 год?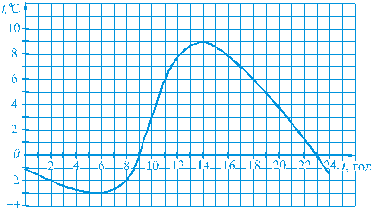

 Рис. 21
Рис. 21
 Рівень В
Рівень В де -3 £ x £ 3;
де -3 £ x £ 3; де -3 £ x £ 3.
де -3 £ x £ 3.
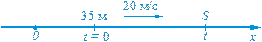

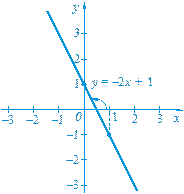 Рис. 24
Рис. 24
 Рис. 25
Рис. 25
 Знайдемо координати якої-небудь точки графіка, відмінної від початку координат: якщо х = 3, то у = 1. Позначимо на координатній площині точку (3; 1) і проведемо через неї та через початок координат пряму (рис. 26). Ця пряма є графіком функції
Знайдемо координати якої-небудь точки графіка, відмінної від початку координат: якщо х = 3, то у = 1. Позначимо на координатній площині точку (3; 1) і проведемо через неї та через початок координат пряму (рис. 26). Ця пряма є графіком функції 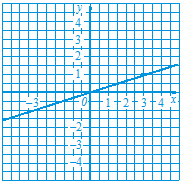

 Для тих, хто хоче знати більше
Для тих, хто хоче знати більше 6. Точки перетину графіків функцій. На рисунку 28 зображені графіки двох лінійних функцій у = –0,25 х + 4 та у = х – 1. Якщо х = 4, то функції набувають одного й того ж значення у = 3. Отже, графіки функцій мають спільну точку (4; 3). Ще кажуть, що графіки перетинаються в точці (4; 3). Взагалі, графіки двох функцій мають спільну точку, якщо існує значення х, для якого обидві функції набувають одного й того ж значення.
6. Точки перетину графіків функцій. На рисунку 28 зображені графіки двох лінійних функцій у = –0,25 х + 4 та у = х – 1. Якщо х = 4, то функції набувають одного й того ж значення у = 3. Отже, графіки функцій мають спільну точку (4; 3). Ще кажуть, що графіки перетинаються в точці (4; 3). Взагалі, графіки двох функцій мають спільну точку, якщо існує значення х, для якого обидві функції набувають одного й того ж значення.




