Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування задач за допомогою рівняньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо приклади. Задача 1.У двох цистернах зберігається 66 т бензину, до того ж, у першій
1,2 х + х = 66. Розв’яжемо це рівняння: 2,2 х = 66; х = 66: 2,2; х = 30. Отже, у другій цистерні є 30 т бензину, а в першій — 1,2 × 30 = 36 (т). Відповідь. 36 т, 30 т. ● Зауваження. Щоб розв’язати задачу 1, можна міркувати й так. Нехай у другій цистерні є х т бензину, тоді в першій ¾ (66 - х) т. У першій цистерні бензину в 1,2 разу більше, ніж у другій, тому 66 - х = 1,2 х. Далі залишається розв’язати це рівняння і записати відповідь до задачі. Задача 2.З міста А в місто В виїхав вантажний автомобіль. Через 30 хв назустріч йому з міста В виїхав легковий автомобіль, швидкість якого на 25 км/год більша, ніж вантажного. Автомобілі зустрілися через 1,3 год після виїзду вантажного автомобіля з міста А. Знайти відстань між ●Нехай швидкість вантажного автомобіля дорівнює х км/год, тоді швидкість легкового ¾ (х + 25) км/год. До моменту зустрічі вантажний автомобіль був у дорозі 1,3 год, а легковий на 30 хв = 0,5 год менше: 1,3 год - 0,5 год = 0,8 год. За 1,3 год вантажний автомобіль проїхав 1,3 х км, а легковий за 0,8 год.— 0,8(х + 25) км. Оскільки вантажний автомобіль проїхав на 10 км більше, ніж легковий, то різниця шляхів 1,3 х км і 0,8(х + 25) км дорівнює 10 км.
Маємо рівняння: 1,3 х - 0,8(х + 25) = 10. Розв’яжемо це рівняння: 1,3 х - 0,8 х - 20 = 10; 0,5 х = 30; х = 60. Отже, швидкість вантажного автомобіля дорівнює 60 км/год. Відстань між містами дорівнює сумі відстаней, які проїхали обидва автомобілі, тобто (1,3 х + 0,8(х + 25)) км. Знайшовши, що х = 60, матимемо: 1,3 х + 0,8(х + 25) = 1,3 × 60+ 0,8 × (60 + 25) = 78 + 68 = 146 (км). Відповідь. 146 км. ● Примітка. Спираючись на розв’язання задач 1 і 2, проаналізуємо перші два кроки наведеної вище схеми розв’язування задач за допомогою рівнянь. 1) Вибір невідомого, яке ми позначали буквою, у розв’язаннях цих задач був різний. У задачі 1 ми позначили через х т одну з шуканих величин (масу бензину в другій цистерні). У задачі 2 шуканою величиною є відстань між містами. Якщо цю величину позначити через х км, то при складанні рівняння доведеться провести доволі складні міркування. Ми ж через х км/год позначили невідому швидкість вантажного автомобіля, виразили через х шляхи, які проїхали автомобілі, й склали рівняння, знаючи, що різниця шляхів дорівнює 10 км. Отже, позначати через х (або якою-небудь іншою буквою) бажано ту невідому величину, через яку легше виражаються величини, значення яких можна прирівняти. 2) Щоб скласти рівняння, спочатку виражаємо через х ті величини, значення яких прирівнюватимемо. Після цього записуємо рівняння. Математична модель. Вам, мабуть, уже доводилося бачити моделі човна, літака, автомобіля, виготовляти моделі куба, прямокутного паралелепіпеда. Кожна модель, залежно від її призначення, відображає певні властивості оригіналу. Математична модель — це опис якогось реального об’єкта чи процесу мовою математики. Опишемо мовою математики задачу 2. Шукаючи швидкість вантажного автомобіля у цій задачі, ми позначили її через х км/год. Швидкість легкового автомобіля на 25 км/год більша, ніж швидкість вантажного, що мовою математики записується так: швидкість легкового автомобіля дорівнює (х + 25) км/год. Мовою математики шлях, який проїхав вантажний автомобіль, записується: 1,3 х км, а шлях, який проїхав легковий автомобіль, — 0,8(х + 25) км. За умовою задачі вантажний автомобіль проїхав на 10 км більше, ніж легковий, що мовою математики можна висловити так: різниця шляхів, які проїхали вантажний і легковий автомобілі, дорівнює 10 км і записати: Одержане рівняння і є математичною моделлю задачі на рух автомобіля. Побудувавши математичну модель, ми звели задачу на рух до математичної задачі — розв’язати рівняння. Крім рівнянь, є й інші види математичних моделей, з якими ми ознайомимося при подальшому вивченні алгебри. Історія науки знає чимало прикладів, коли в межах вдало побудованої математичної моделі за допомогою обчислень, як кажуть, «на кінчику пера», вдавалося передбачити існування нових фізичних об’єктів та явищ. Так, спираючись на математичні моделі, астрономи Дж. Адамс (Англія) у 1845 році й У. Левер’є (Франція) у 1846 році незалежно один від одного дійшли висновку про існування невідомої тоді ще планети і вказали її розміщення. За розрахунками Левер’є астроном Г. Галле (Німеччина) знайшов цю планету. Її назвали Нептуном.
70. У двох мішках є 68 кг картоплі, до того ж, у першому мішку на 12 кг картоплі більше, ніж у другому. Скільки картоплі в кожному мішку? 71.У двох комп’ютерних класах є разом 33 комп’ютери, до того ж, в одному класі їх у 1,2 разу більше, ніж в іншому. Скільки комп’ютерів у кожному класі? 72. Агрофірма відвела під цукровий буряк землі у 3,5 разу більше, або на 560 га більше, ніж під картоплю. Скільки землі відвела агрофірма під цукровий буряк і скільки — під картоплю? 73. Батько утричі старший від сина. Відомо також, що він на 24 роки старший від сина. Скільки років батькові та скільки синові? 74. Два робітники виготовили 36 деталей, до того ж, кількість деталей, які виготовив перший робітник, становить 0,8 кількості деталей, які виготовив другий. Скільки деталей виготовив кожен робітник? 75. Оператор набрав на комп’ютері половину рукопису за 15 год. Другу половину рукопису він набрав на 2,5 год швидше, бо набирав за годину на 2 сторінки більше. Скільки сторінок має рукопис? 76.Перший автомобіль долає шлях між двома містами за 1,5 год, а другий за 1,2 год. Швидкість другого автомобіля більша від швидкості першого на 15 км/год. Знайдіть відстань між містами. 77. Периметр трикутника дорівнює 25 см. Знайдіть довжину кожної сторони трикутника, якщо: а) перша сторона в 1,5 разу довша від другої, а друга ¾ на 4 см коротша від третьої; б) довжина першої сторони на 5 см більша від довжини другої, а довжина третьої ¾ на 7 см менша від суми довжин перших двох. 78.Олег, Сергій та Віталій купили футбольний м’яч, ціна якого дорівнює 12 грн., до того ж, Олег витратив грошей на 2 грн. менше, а Сергій ¾ в 1,5 разу більше, ніж Віталій. Скільки грошей витратив на купівлю м’яча кожен хлопець? 79. Магазин продав за 3 дні 460 кг овочів. За другий день було продано овочів на 20 кг більше, ніж за перший, а за третій ¾ в 1,2 разу більше, ніж за другий. Скільки овочів продав магазин за кожний день окремо? 80.У трьох мішках є 135 кг цукру, до того ж, у першому на 15 кг більше, ніж у третьому, а в третьому в 1,2 разу менше, ніж у другому. Скільки цукру в кожному мішку?
81. Перший велосипедист долає шлях між двома селами за 36 хв, а другий ¾ за 45 хв. Швидкість першого велосипедиста більша від швидкості другого на 4 км/год. Знайдіть швидкість кожного велосипедиста і відстань між селами.
82. У першій корзині було на 12 яблук більше, ніж у другій. Після того як мама взяла з першої корзини 18 яблук, а з другої ¾ 14, у першій корзині яблук стало в 1,2 разу більше, ніж у другій. Скільки яблук було в кожній корзині спочатку? 83. З Чернівців одночасно виїхали два автомобілі й одночасно приїхали до Житомира. Перший автомобіль їхав зі сталою швидкістю. Другий же автомобіль перші 2 год їхав зі швидкістю на 12 км/год меншою, а решту 3 год ¾ зі швидкістю, в 1,1 разу більшою від швидкості першого автомобіля. Знайдіть відстань між містами. 84.З міста А до міста В одночасно виїхали автомобіль і мотоцикліст. Коли через 2,5 год автомобіль прибув до міста В, мотоциклісту до цього міста залишалося проїхати ще 75 км. Знайдіть відстань між містами, якщо швидкість автомобіля в 1,6 разу більша від швидкості мотоцикліста. 85. Човен проплив шлях між двома пристанями за течією річки за 1,2 год, а на зворотний шлях затратив 1,5 год. Знайдіть відстань між пристанями, якщо швидкість човна у стоячій воді дорівнює 22,5 км/год.
87. Автомобіль мав подолати шлях завдовжки 140 км за 2 год. Деяку частину шляху він проїхав зі швидкістю 60 км/год, а решту шляху ¾ зі швидкістю 75 км/год. Скільки кілометрів проїхав автомобіль зі швидкістю 60 км/год, якщо відомо, що до місця призначення він прибув вчасно? 88.Зі Львова до Києва, відстань між якими 520 км, вийшов поїзд, а через годину назустріч йому з Києва вийшов другий поїзд, який проходить за годину на 4 км більше, ніж перший. Поїзди зустрілися через 4 год після відходу другого поїзда з Києва. Знайдіть швидкість кожного поїзда. Вказівка. Розв’язуючи задачу, використайте схему:
89. Дідусь старший від свого внука в 4 рази. Якби дідусь був на рік молодший, то був би старшим від своєї внучки у 5 разів. Скільки років дідусеві, внукові й онучці, якщо внучка на 3 роки молодша від онука? 90.На двох полицях стояло 95 книжок. Коли четверту частину книжок, що були на першій полиці, переставили на другу, то на другій полиці книжок стало на 5 більше, ніж на першій. Скільки книжок стояло на кожній полиці спочатку? 91. У школі є три сьомих класи. Кількість учнів 7-А класу становить 35% від кількості всіх семикласників, а у 7-Б класі на 2 учні менше, ніж у 7-А. Скільки семикласників є у школі, якщо у 7-В класі навчається 26 учнів? 92.За зміну 3 робітники виготовили партію деталей. Перший робітник виготовив 30% усіх деталей, другий ¾ на 5 деталей менше, ніж третій, і на 2 деталі більше, ніж перший. Скільки всього деталей виготовили робітники? 93. Вранці вкладник зняв з рахунку в банку
94. Біля будинку стоять дві бочки, місткість кожної з яких дорівнює 100 л. У першій бочці є 20 л дощової води, а в другій ¾ 15 л. Пішов дощ, і щохвилини в першу бочку вливається 2 л води, а в другу ¾ 2,5 л. Через скільки хвилин води в бочках буде порівну? Знайдіть два варіанти відповіді.
95. За легендою, Піфагор на запитання про число учнів, що відвідують його школу, відповів так: «Половина учнів вивчає математику, чверть ¾ музику, сьома частина перебуває в мовчанні і, крім того, є ще три жінки». Скільки учнів було в Піфагора? 96. Зелена маса для силосу повинна мати певну вологість. Щоб вийшла така маса, змішують у певному співвідношенні рослини з різним вмістом води. Скільки потрібно взяти зеленої маси з вологістю 85% і маси з вологістю 35%, щоб одержати 1 т маси з вологістю 75%? 97. У двох бідонах є 70 л молока. Коли 12,5% молока, що було в першому бідоні, перелили у другий, то в обох бідонах молока стало порівну. Скільки літрів молока було в кожному бідоні спочатку? 98. Сплав міді, цинку й олова містить 32% олова, а міді ¾ на 40 г менше, ніж олова. Відомо також, що цинку в сплаві на 100 г більше, ніж міді. Знайдіть масу сплаву. 99. У процесі очищення руди кількість домішок у ній зменшується від 20% у добутій руді до 5% в очищеній. Скільки потрібно взяти добутої руди, щоб одержати 32 т очищеної? Вправи для повторення 100. Запишіть: а) суму числа m і числа, протилежного числу n; б) різницю числа s і числа, протилежного числу - t; в) добуток найбільшого від’ємного цілого числа і суми чисел а та b. 101. До частки чисел -1,8 і –1,3 додайте добуток чисел 4,8 і –1,05. 102. Знайдіть значення виразу 2 x 2 - 4 y 2, якщо х дорівнює найменшому цілому числу, яке задовольняє нерівність -5,4 < x < -2,7, а y ¾ найбільшому цілому числу, яке задовольняє нерівність -15,4 £ у £ -2. 103. Поставте замість зірочок такі цифри, щоб число: а) 1* 48 ділилося на 9; б) 3* 4* ділилося на 3 і на 5. 104. Розкрийте дужки і зведіть подібні доданки: а) х - (х - 1) + (х + 1); б) 2(1,5 а - 2(а - 1,5)); в) 2(a + 2 b + 3 c) - (a + 3 b + 5 c) – (a + b + c). 105. Оленка має фломастери шести кольорів. Скількома способами вона може написати число 2002 так, щоб різні цифри мали різний колір, а однакові цифри — однаковий колір?
Протягом багатьох століть алгебра була наукою про рівняння та способи їх розв’язування. Лінійні рівняння вміли розв’язувати ще давні єгиптяни й вавилоняни (І тис. до н.е.). Про стан математики в Давньому Єгипті можна дізнатися з математичних текстів, написаних на особливому папері — папірусі, виготовленому зі стебел рослини, яка має таку ж назву. Написання деяких папірусів відносять до XVIII ст. до н. е., хоча описані в них математичні факти були відомі давнім єгиптянам задовго до їх написання. Один з таких папірусів був знайдений у 1872 році в одній з єгипетських пірамід. Його придбав англійський колекціонер предметів старовини Райнд і зараз цей папірус — папірус Райнда — зберігається в Лондоні. У папірусі Райнда особливе місце посідають задачі на «аха» («хау»).
Починаючи із VII ст. до н. е., давні греки, ознайомившись з досягненнями єгиптян і вавилонян в галузі математики, продовжили їх науку. Проте доволі мало грецьких вчених для розв’язання задач використовували рівняння. Одним із тих, хто використовував рівняння, був давньогрецький математик Діофант. Про Діофанта відомо небагато, навіть точно не встановлено роки його життя. Дещо про його життя і про те, скільки він прожив років, можна судити з напису на його могильній плиті.
Грецьку науку в середні віки перейняли вчені Сходу — індійці та араби. Саме на Сході в IX ст. алгебра стає самостійною математичною наукою. Походження слова «алгебра» також пов’язане зі Сходом. Місто Багдад у VII–IX ст. було столицею могутнього Арабського халіфату. Багдадські халіфи сприяли розвитку природничих і математичних наук. За панування халіфа Гаруна ал-Рашида в Багдаді була заснована велика бібліотека, а халіф ал-Мамун організував своєрідну академію — «Будинок мудрості» й побудував добре обладнану обсерваторію.
У XII ст. твір ал-Хорезмі переклали латинською мовою, зберігши в його назві лише слово «ал-джебр», яке згодом стали вимовляти як алгебра. Поступово сформувалася сучасна алгебра, яка охоплює не тільки теорію розв’язування рівнянь, а й способи проведення операцій (дій) з різноманітними об’єктами (зокрема, із числами). Запитання і вправи для повторення § 1 1. Наведіть приклади рівнянь. 2. Що називають коренем рівняння? Чи є число 4 коренем рівняння 3 х - 2 = х + 6? 3. Що означає розв’язати рівняння? 4. Сформулюйте властивості рівнянь. 5. Дайте означення лінійного рівняння. Наведіть приклад лінійного 6. Скільки коренів може мати лінійне рівняння? 106. Доведіть, що число 2,5 є коренем рівняння: а) 3 x - 5 = x; б) х (х - 0,5) = 4 х - 5. 107. Яке з чисел -2; -1,2; 1,8 є коренем рівняння 5 x - 3 = 10 x + 3? 108. Скільки коренів має рівняння: а) Розв’яжіть рівняння: 109. а) 2 х - 3 = 5(x - 3); б) 12(х - 1) = 24(x + 1); в) 0,6(2 х - 3) - 1,5(х + 4) = -4,2 x; г) 2(3 - 2(x + 1)) = 6(2 - х); д) є) 110*. а) 2| х | + 0,2 = в) | х - 2| = 2; г) 3|2 х + 1| - 7 = 2. 111 *. а) 5 x – 2| х | = 21; б) 2(| х | - 5) = 3 x – 7. 112. Периметр прямокутника дорівнює 48 см, до того ж, його довжина втричі більша від ширини. Знайдіть площу прямокутника. 113. Периметр трикутника дорівнює 30 см. Знайдіть довжину кожної сторони трикутника, якщо перша його сторона на 4 см коротша від другої, а друга ¾ в 1,2 разу довша від третьої. 114. Трактор зорав поле за 3 дні. За перший день було зорано 35% площі поля, за другий ¾ на 4 га менше, ніж за перший, а за третій день ¾ 25 га. Знайдіть площу поля. 115. Теплохід пройшов шлях завдовжки 90 км. Деяку частину цього шляху теплохід йшов зі швидкістю 30 км/год, а решту ¾ зі швидкістю 25 км/год. Який шлях пройшов теплохід зі швидкістю 30 км/год, якщо на весь шлях він затратив 3,5 год? 116*. Туристу треба пройти шлях від села до станції завдовжки 10 км. Коли він вийшов із села, до відходу поїзда, на який він поспішав, залишалося 3 год. Долаючи 3 км за годину, турист зрозумів, що запізнюється на поїзд, і пішов зі швидкістю 4 км/год. На станцію він прийшов за 12 хв до відходу поїзда. Скільки часу рухався турист зі швидкістю 3 км/год? 117*. Є два сплави міді й олова; перший містить 40% міді, а другий ¾ 60%. Скільки потрібно взяти кожного сплаву, щоб одержати 10 кг нового сплаву, який містив би 54% міді? 118*. За першу поїздку автомобіль витратив 25% бензину, що був у баку, за другу ¾ на 40% менше, ніж за першу. Після цього в баку залишилося бензину на 8 л більше, ніж було витрачено за обидві поїздки. Скільки літрів бензину було в баку спочатку? Завдання для самоперевірки № 1 Рівень 1. Яке з чисел є коренем рівняння 4 x + 2 = 10? а) 1; б) -2; в) 2; г) 3. 2. Скільки коренів має рівняння (x - 2)(x + 2) = 0? а) Один; б) два; в) безліч; г) коренів немає. 3. Які з даних рівнянь є лінійними рівняннями? а) 4. Розв’яжіть рівняння 7 y – 3 = 3 y + 5 та вкажіть правильну відповідь: а) -2; б) 2; в) 0,8; г) 0,5. 5. Книжка й альбом коштують 6 грн., до того ж, книжка в 4 рази дорожча від альбому. Яке з рівнянь треба скласти, щоб знайти ціну альбому (х ¾ ціна альбому в гривнях)? а) x + 6 х = 4; б) 6 x - х = 4; в) x + 4 х = 6; г) 4 x - х = 6. Рівень 1. Складіть лінійне рівняння, коренем якого є число 3. 2. Скільки коренів має рівняння: а) 7 x = 1; б) 0 × x = –2; в) 2 x = 0; г) 0 × x = 0? 3. Розв’яжіть рівняння: а) 2(x - 3) = 5 x - 9; б) 4 - 5(1 - 2 х) = 1 - 6 х. 4. Швидкість велосипедиста на 10 км/год більша від швидкості пішохода. Відомо, що за 2 год велосипедист долає таку ж відстань, яку пішохід проходить за 6 год. Знайдіть швидкість пішохода. Рівень 1. Чи мають рівняння (x - 1)(x + 2) = 0 і x + 2 = 0 одні й ті ж корені? 2. Розв’яжіть рівняння: а) 160 х + 560 = -160(3 x - 1); б) 3. У двох сувоях є 81 м тканини, до того ж, у першому — на 70% більше, ніж у другому. Скільки метрів тканини у кожному сувої? 4. У першому резервуарі є 420 м3 води, а у другому ¾ 750 м3. З обох резервуарів почали одночасно випускати воду. З першого резервуара щогодини витікає 28 м3 води, а з другого ¾ 38 м3. Через скільки годин у першому резервуарі стане вдвічі менше води, ніж у другому? Рівень 1. Доведіть, що рівняння 2. Розв’яжіть рівняння: а) 3. Екскаватор мав вирити траншею певної довжини. За перший день він вирив 30% довжини всієї траншеї, за другий ¾ на 10% більше, ніж за перший, а за третій ¾ решту 111 м. Знайдіть довжину траншеї. 4. Сплав міді й олова має масу 12 кг і містить 45% міді. Скільки кілограмів олова потрібно додати до цього сплаву, щоб одержати новий сплав, який містив би 40% міді?
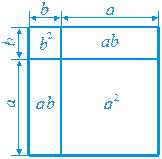
(a + b)2 = a 2 + 2 ab + b 2
ЦІЛІ ВИРАЗИ
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.117 (0.266 с.) |


 Рівень А
Рівень А Рівень Б
Рівень Б
 86. Від пристані А до пристані В за течією річки катер плив 3 год, а від В до А ¾ 4 год. Знайдіть швидкість катера у стоячій воді, якщо швидкість течії дорівнює 3 км/год.
86. Від пристані А до пристані В за течією річки катер плив 3 год, а від В до А ¾ 4 год. Знайдіть швидкість катера у стоячій воді, якщо швидкість течії дорівнює 3 км/год.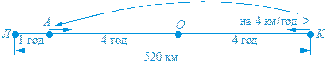
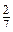 усіх грошей, а після обіду — 30% залишку. Після цього на його рахунку залишилося 175 грн. Який був початковий вклад?
усіх грошей, а після обіду — 30% залишку. Після цього на його рахунку залишилося 175 грн. Який був початковий вклад? Рівень В
Рівень В

 , її
, її  , її
, її  і її ціле. Це 33». Якщо позначити «купу» — невідому величину — через x, то за цією задачею одержимо рівняння:
і її ціле. Це 33». Якщо позначити «купу» — невідому величину — через x, то за цією задачею одержимо рівняння:  .
. Діофант (ІІІ ст.),
давньогрецький математик
з Александрії
Діофант (ІІІ ст.),
давньогрецький математик
з Александрії



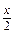
 Мухаммед бен Муса ал-Хорезмі (IX ст.),
арабський математик,
астроном і географ.
Уперше розглядає алгебру
як самостійний розділ
математики
Мухаммед бен Муса ал-Хорезмі (IX ст.),
арабський математик,
астроном і географ.
Уперше розглядає алгебру
як самостійний розділ
математики
 x = 12; б)
x = 12; б)  = 1; в) 0(x + 3) = 0?
= 1; в) 0(x + 3) = 0? (2 х + 5) + 0,25(х + 3) =
(2 х + 5) + 0,25(х + 3) =  е) 24(х - 3) + 18(x - 2) = 30(3 х - 10);
е) 24(х - 3) + 18(x - 2) = 30(3 х - 10); ж)
ж) 
 б) 3 - 2(1- 2| х |) = 11 - | х |;
б) 3 - 2(1- 2| х |) = 11 - | х |;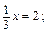 б) y 2 = 4; в) 2: х = 3; г) –2 y = 0.
б) y 2 = 4; в) 2: х = 3; г) –2 y = 0.
 і
і  мають одні й ті ж корені.
мають одні й ті ж корені. б) 2(| х | - 3) = 4| х | - 10.
б) 2(| х | - 3) = 4| х | - 10.