
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі за курс алгебри 7 класуСодержание книги
Поиск на нашем сайте
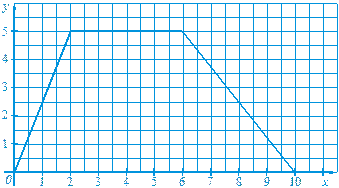
1047. Купили 2 кг огірків по а грн. за кілограм і 5 кг помідорів по b грн. за кілограм. Запишіть у вигляді виразу вартість покупки. 1048. Автомобіль протягом t год рухався зі швидкістю 80 км/год і протягом 2 год — зі швидкістю 70 км/год. Запишіть у вигляді виразу шлях, який проїхав автомобіль за весь час руху. Знайдіть значення цього виразу, якщо t = 1,2. 1049. Через першу трубу до басейну щохвилини поступає а л води, а через другу — b л. Скільки літрів води поступить до басейну через обидві труби за 3 год? 1050. Знайдіть значення степеня: а) 94; б) (-3)5; в) (-2,5)3; г) 1051. Подайте у вигляді степеня з основою а: a) а 2 а 4; б) а 7: а; в) (а 3)5; г) (а 5 × а)4. 1052. Обчисліть: а) 0,45 × 2,55; б) (22 × 0,52)7 × 0,254 × 44; в) 1053. Подайте одночлен у стандартному вигляді та вкажіть його степінь: a) 8 х 2 ху; б) -3 а 2 b × 2(а 5)2; в) - m 3 × 3 m 2 n × 5 n 4; г) 0,5 ас × (-4 а 3 с)2 × а 2 с; д) 1054. Подайте одночлен 12 a 4 b 5 у вигляді добутку двох одночленів стандартного вигляду, одним з яких є: 2 a 2 b 2; -4 a 3 b; -0,5 b. 1055. Подайте одночлен 9 a 6 b 2 у вигляді квадрата одночлена. 1056. Подайте одночлен 27 х 6 у 9 у вигляді куба одночлена. 1057. Знайдіть значення одночлена: а) -4 а 3 b, якщо а = 1058*. Спростіть вираз, де n — натуральне число: а) (х 3)3 n × (х 5 хn + 1)2; б) (- аn)17 × (- a 2)9. 1059. Запишіть многочлен у стандартному вигляді та знайдіть його степінь: а) 3 x 2- 6 х + х 2 - 3 + x; б) 3 а × 2 ab + a 5 - a 3 - 7 a 2 b ; в) 0,6 a 2 b - 1,4 b 2 a + 2,8 а 2 b + 3,3 аb 2; г) 5 x 3+ 1060. Спростіть вираз: а) 8 а 2 + 4 а - 3 - (7 - 8 а + 3 а 2); б) х - 3 х 2 у - ху + (х 2 - 3 х 2 у + ху); в) Виконайте множення: 1061. а) 4 а (а 2 - 4 а + 3); б) (2 х 2 - 4 х + 8)(-0,5 х 2); в) (4 ab 2+ 9 а 2)(2 b 2 - 3 a); г) (a - 7)(b + 1)(c - 2). 1062.а) (b + 2 c)(b - 2 c); б) (5 x - 2 y)(5 x + 2 y); в) (1,4 a - 0,3 b)(0,3 b + 1,4 a); г) 1063. Піднесіть до квадрата: а) (2 х + 3)2; б) (3 с - 1)2; в) (0,4 b - 5 а)2; г) Спростіть вираз: 1064. а) (х - 3)(х 2 + х + 3) - х 3; б) 3 с - (с - 2)(2 с 2 - с + 1) - 5 с 2; в) (5 + х)(5 - х) + х 2; г) (2 b - 9)(2 b + 9) - 4 b 2; д) (n - 1)(n 2 + n + 1)- n 3; е) (а + 3)(а 2 - 3 а + 9)- 27. 1065. а) (10 - 3 m)(2 + 3 m) + (5 m - 4)(5 - 2 m); б) (4 a + 9)(a 2 - 2 a + 2) - (4 a - 7)(а + 1)2; в) (n 2 - 3 n)(1 + 3 n)(-1 + n) - 3 n (n 3 + 1); г) (4 y - 5 y 2)2 + (2 y + 5 y 2)2 - 20 y 2. Запишіть у вигляді многочлена стандартного вигляду: 1066. а) (b + 2)(b - 2)(b 2+ 4); б) 15 х 3(х 2+ 10)(10 - х 2); в) а 5(а 4 - (2 а 3 + а 2(а 2 - 2 а + 3))) + 4 а 7. 1067*. а) (а 2 + 2 а - 2)2; б) (5 x - 2)3; в) (с - 3)4. 1068. Доведіть тотожність: а) у (b - x) + x (b + y)= b (x + y); б) (- m + n)(m - n) = -(n - m)2; в) (a + b + c + d)2 – (a + b)2 - (c + d)2 = 2(a + b)(c + d); г) (n + 1)(n + 3)(n + 5)(n + 7) + 7 = (n 2 + 8 n + 8)(n 2 + 8 n + 14). Розкладіть на множники: 1069. а) 2 x + 2 ху; б) а 2- 2 а; в) 12 xу 3+ 8 ху 2 - 16 х 2 у. 1070. а) ах - ay + 3 x - 3 y; б) x 2 у – 2 х + xy - 2; в) 9 уа - 6 yа 2 + 2 axy - 3 xy; г) 8 x 2 a – 15 y 3 - 10 x 2 y + 12 ay 2. 1071. а) 9 n 2 - 4 m 2; б) 120 – 30 a 4; в) 27 х 3 + 0,008 у 3; г) х 3 - (m - n)3; д) a 2 + 8 а + 16; е) 6 х 2- 24 ху + 24 у 2. 1072. a) 1073*. а) x 2- 2 x – 3; б) а 2+ 3 а – 4; в) х 2- 8 ху + 7 у 2. 1074. Доведіть, що значення виразу: а) 97 - 312 ділиться на 8; б) 498 + 3 × 715 ділиться на 10. 1075. Обчисліть: а) 97 × 103; б) 1,8 × 2,2; в) 522 – 482; г) 7,352 – 6,352. 1076. Знайдіть значення виразу: а) а 3 - 0,5 а 2, якщо а = 1,5; б) х 2 – 2 xy + y 2, якщо x = -0,3; y = 10,3. 1077. Доведіть, що значення виразу (х + 1)2 - (х - 1)(х + 3) не залежать від значень х. 1078. Доведіть, що для будь-якого цілого значення n значення виразу: а) (2 n + 3)2 - (2 n - 1)2 ділиться на 8; б) (8 n - 4)2 - 8(4 n - 3) не ділиться на 32. 1079. Для якого значення х значення виразу х 2 + 2 х + 9 є найменшим? 1080. Для якого значення х значення виразу 2 - х 2 + 4 х є найбільшим? 1081*. Доведіть, що сума кубів двох послідовних цілих чисел, які не діляться на 3, кратна 9. 1082*. Чи може різниця четвертих степенів двох натуральних чисел бути 1083*. Знайдіть найменше значення виразу х 2+ у 2 - 4 у - 2 x. 1084*. Доведіть, що коли деякі два цілі числа не діляться на 3, то їх сума або різниця діляться на 3. 1085*. Два велосипедисти проїхали шлях від пункту А до пункту В. Перший велосипедист першу половину шляху їхав зі швидкістю 20 км/год, а другу половину ¾ зі швидкістю 16 км/год. Другий же велосипедист першу половину шляху їхав зі швидкістю 19 км/год, а другу половину ¾ зі швидкістю 17 км/год. Хто з них затратив більше часу на шлях від А до В? Розв’яжіть рівняння: 1086. а) 3 х - 18 = 57- 2 х; б) 3(x – 2) – 4(х - 4) = 5; в) 250(х + 8) = 125 х – 500; г) 0,3(1 – x) = 0,4(х - 1) – 0,7; д) є) 1087. а) х (х + 5) – х 2 = 2; б) (2 х + 3)(х – 1) = 2 х 2; в) х (х + 0,1) = (х – 0,1)(х + 0,2); г) д) (х – 3)(х + 3) = (х + 1)2; е) 2 х (х – 1,5)2 = 2 х 3 – 6 х 2 + 3. 1088. a) у 3 - 3 у 2 = 0; б) х 3 - в) х 2 – 6 х + 9 = 0; г) х 3 – 2 х 2 – 4 х + 8 = 0; д) у 2 + 2 у – 48 = 0; е) 1089*. а) |3 - 2 x | = 5; б) || х | - 2| = 6. 1090*. а) (| х | + 5)(3| х | - 9) = 0; б) | x (х - 2)| + х 2 = 0; в) х 2 + 2| х | + 1 = 0. 1091*. Доведіть, що рівняння x 4+ 1 + (x - 2)4 = 2 х 2не має коренів. 1092*. Розв’яжіть рівняння Розв’яжіть задачі 1093–1098, склавши рівняння. 1093. Периметр прямокутника дорівнює 68,4 см. Знайдіть сторони прямокутника, якщо одна з них на 3,6 см коротша від іншої. 1094. Сума двох чисел дорівнює 52,7, одне з них у 2,4 разу більше від другого. Знайдіть більше із цих чисел. 1095. У першій цистерні втричі більше бензину, ніж у другій. Коли з першої цистерни забрали 400 л бензину, а з другої — 800 л, виявилося, що в перший цистерні бензину стало у 8 разів більше, ніж у другій. Скільки бензину було в кожній цистерні спочатку? 1096. З міста виїхав мотоцикліст і рухався зі швидкістю 40 км/год. Через півгодини услід за ним виїхав автомобіль, швидкість якого дорівнює 60 км/год. Через скільки годин після свого виїзду з міста автомобіль наздожене мотоцикліста? 1097. Нержавіюча сталь є сплавом заліза, хрому й нікелю. Лист з такої сталі містить 15% хрому, 0,5% нікелю, а заліза — на 2,78 кг більше, ніж хрому. Знайдіть масу листа. 1098*. Автобус рухався до міста N зі швидкістю 60 км/год. Дорогою його обігнав легковий автомобіль, що їхав зі швидкістю 80 км/год. Автомобіль прибув до міста N і через 15 хв вирушив у зворотний шлях. На відстані 10 км від міста N він знову зустрів автобус. На якій відстані від міста N були автобус і автомобіль при першій зустрічі? 1099. Функція задана формулою у = –2 х + 3. а) Знайдіть значення функції, які відповідають таким значенням аргументу: –2; 0; 6. б) Знайдіть значення аргументу, якому відповідає значення функції: 3; 1. в) Для якого значення х значення функції дорівнює значенню аргументу? 1100. Побудуйте графік функції у = 2 х – 0,5. За допомогою графіка знайдіть: а) значення функції, якщо х = –0,5; х = 1,5; б) значення х, для якого у = 1,5. 1101. Побудуйте графік функції у = 0,5 х + 1, де -4 £ x £ 3. Яка область визначення та область значень функції? Чому дорівнюють найбільше та найменше значення функції? Вкажіть нулі функції. Для яких значень х функція набуває додатних значень; від’ємних значень? 1102. Побудуйте графік функції: а) у = – х + 1, де -3 £ x £ 2; б) y = 2 х 2 – 2, де -2 £ x £ 2. в) у = 1,5 х; г) у = –1,5 х; д) у = 3 х + 1; е) у = –1,5 х – 1. 1103. Графік прямої пропорційності проходить через точку A (2; 7). Чи проходить цей графік через точку B (-4; -14)? 1104. На рисунку 47 зображено графік функції. Знайдіть область визначення та область значень цієї функції. Задайте функцію формулою, якщо: а) 0 £ х £ 2; б) 2 £ х £ 6.
1105. Знайдіть координати точок перетину графіків функцій: а) у = 1,5 х і у = – х + 5; б) у = –2 х і y = х 2. 1106. Для якого значення b графіки функцій у = 3 х + b і у = 2 х + 4 перетинаються в точці, що лежить на осі абсцис? 1107. Чи є пара чисел (2; –1) розв’язком рівняння 2 х + 5 у = -3? 1108. Побудуйте графік рівняння: а) х + 3 у = 3; б) 2 х - 3 у = 6; в) 2 х = 5; г) -3 у = 6. 1109. Розв’яжіть графічно систему рівнянь Розв’яжіть систему рівнянь: 1110. а) 1111. а) 1112. а) 1113. Знайдіть точку перетину графіків рівнянь 2 х + 3 у = -2 і 4 х - 5 у = 7. 1114. Чи належить точка перетину графіків рівнянь 2 х + 4 у = -6 і 10 х - у = 12 графіку рівняння 3 х + у = 1? 1115. Графік лінійної функції проходить через точки A (-1; 1) і B (3; -7). Задайте цю функцію формулою. 1116*. Для якого значення k система рівнянь Розв’яжіть задачі 1117–1121, склавши систему рівнянь. 1117. Сума двох чисел дорівнює 20,5, одне з них на 2,3 більше від іншого. Знайдіть ці числа. 1118. Два автоматичні станки за 8 год спільної роботи виготовляють 2000 деталей. Перший станок за 2 год і другий за 3 год разом виготовляють 630 деталей. Скільки деталей виготовляє за годину кожний станок? 1119. З пунктів А і В, відстань між якими дорівнює 17 км, вийшли назустріч один одному два туристи і зустрілися через 2 год. Знайдіть швидкості туристів, якщо швидкість одного з них на 0,5 км/год менша від швидкості іншого. 1120. Братові й сестрі разом 10 років. Скільки років кожному з них, якщо через рік брат буде вдвічі старший від сестри? 1121*. Молоко однієї корови містить 5% жиру, а іншої — 3,5%. Змішавши молоко обох корів, одержали 10 л молока, жирність якого дорівнює 4%. Скільки для цього використали літрів молока від кожної корови?
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.89.130 (0.007 с.) |



 е)
е) 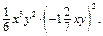
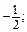 b =
b =  б) (2 х 3 у)2 × у 4, якщо х = 0,25; у = 4.
б) (2 х 3 у)2 × у 4, якщо х = 0,25; у = 4. x 2-
x 2-  x 3-
x 3-  x 2.
x 2.


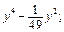 б) а 2- 4 b 2 + 2 b + a; в) х 2- 4 ху + 4 у 2 - 4 у 4.
б) а 2- 4 b 2 + 2 b + a; в) х 2- 4 ху + 4 у 2 - 4 у 4.  е)
е) 
 ж)
ж) 

 х = 0;
х = 0;
 .
.

 б)
б)  в)
в) 
 б)
б) 
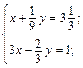 б)
б) 
 має безліч розв’язків?
має безліч розв’язків?


