
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тотожно рівні вирази. ТотожностіСодержание книги
Поиск на нашем сайте
1. Тотожно рівні вирази. Знайдемо значення виразів 5 a - 5 b і 5(a - b), якщо a = 4, b = 2: 5 a - 5 b = 5 × 4- 5 × 2 = 20 - 10 = 10; 5(a - b) = 5 × (4- 2) = 5 × 2 = 10. Значення цих виразів для даних значень змінних дорівнюють одне
Розглянемо тепер вирази 5 a + b і a + 5 b. Якщо a = 1 і b = 1, то відповідні значення цих виразів дорівнюють одне одному: 5 a + b = 5 × 1+ 1 = 6; a + 5 b = 1 + 5 × 1 = 6. Якщо ж a = 2, b = 1, то відповідні значення цих виразів різні: 5 a + b = 5 × 2+ 1 = 11; a + 5 b = 2 + 5 × 1 = 7. Отже, значення виразів 5 a + b і a + 5 b для одних значень змінних дорівнюють одне одному, а для інших — ні. Такі вирази не є тотожно рівними. 2. Тотожності. Якщо два тотожно рівні вирази 5 a - 5 b і 5(a - b) сполучити знаком «=», то одержимо рівність 5 a - 5 b = 5(a - b), яка є правильною для будь-яких значень змінних. Таку рівність називають тотожністю.
Прикладами тотожностей є рівності, які виражають основні властивості додавання і множення чисел:
Тотожностями є також рівності, які виражають правила розкриття дужок:
Тотожностями є й такі рівності:
3. Тотожні перетворення виразів. У виразі 4 a + 3 а - 1 зведемо подібні доданки 4 a і 3 а: 4 a + 3 а - 1 = (4 + 3) а - 1 = 7 a - 1. Вираз 4 a + 3 а - 1 замінили тотожно рівним йому виразом 7 a - 1. Заміну одного виразу тотожно рівним йому виразом називають тотожним перетворенням виразу. У математиці часто доводиться спрощувати вираз, тобто замінювати його тотожно рівним виразом, який має коротший запис або, як кажуть, є «більш компактним». Розглянемо приклади. Приклад 1.Спростити вираз ● Приклад 2.Спростити вираз а + (2 а - 3 b) - (2 - 4 b). ● а + (2 а - 3 b) - (2 - 4 b) = а + 2 а - Підсумок.
Розглянемо приклади. Приклад 3.Довести тотожність а - 3 - (4 а + 7) = -3 а - 10. ● Перетворюватимемо ліву частину рівності: а - 3 - (4 а + 7) = а - 3 - 4 а - 7 = -3 а - 10. Шляхом тотожних перетворень ліву частину рівності звели до правої частини. Тому ця рівність є тотожністю. ● Приклад 4.Довести тотожність 15 = (27 - 5 а) - (12 - 3 а - 2 а). ● Перетворюватимемо праву частину рівності: (27 - 5 а) - (12 - 3 а - 2 а) = 27 - 5 а - 12 + 3 а + 2 а = 15. Шляхом тотожних перетворень праву частину рівності звели до лівої частини. Тому ця рівність є тотожністю. ● Приклад 5.Довести тотожність 2 с + 3 - 2(3 - 2 с) = 3(2 с - 3) + 6. ● Перетворюватимемо ліву і праву частини рівності: 2 с + 3 - 2(3 - 2 с) = 2 с + 3 - 6 + 4 с = 6 с - 3; 3(2 с - 3) + 6 = 6 с - 9 + 6 = 6 с - 3. Шляхом тотожних перетворень ліву і праву частини рівності звели до одного й того ж виразу 6 с - 3. Тому ця рівність є тотожністю. ● Приклад 6.Довести тотожність 3 х - 2(2 х - 3 у) = 2 х + 3(2 у - х). ● Утворимо різницю лівої та правої частин і спростимо її: 3 х - 2(2 х - 3 у) - (2 х + 3(2 у - х)) = 3 х - 2(2 х - 3 у) - 2 х – 3(2 у - х) = = Різниця лівої і правої частин рівності дорівнює нулю, тому дана рівність є тотожністю. ● Усно 172. Чи є тотожно рівними вирази: а) 5 + 6 х і 6 х + 5; б) а × 5 b і 5 ab; в) а - b і b - a? Відповіді обґрунтуйте. 173. Чи є тотожністю рівність: а) аb + 2 = 2 + ab; б) а - 1 = -1 + а; в) 2(а - 3) = 2 а - 3? Відповіді обґрунтуйте. 174. Назвіть кілька виразів, які тотожно рівні виразу х + 4 х. 175. Поясніть, на основі яких правил та яких властивостей дій здійснено такі тотожні перетворення: -2 b - (а - 3 b) + 5 a = -2 b - а + 3 b + 5 a = -2 b + 3 b - а + 5 a = =(-2 + 3) × b + (-1 + 5) × a = b + 4 а. 176. Спростіть вираз: а) -7 + 4 а - 3 а; б) 4 а × 5 b; в) 5 х + (2 - х).
Зведіть подібні доданки: 177. а) 7 а - 3 а + 6; б) -4 + 3 z - 8 z; 178. а) 5 а - 6 + 3 a; б) -3 b + 4 b - 2 b; в) 2 c - 1 + 6 c - 6; г) 1,5 a - 2,5 b + 3,5 a; д) –2 x + 3 y - 6 x - 5 y; е) 3 b - a + 0,6 a + 1,2 a. Розкрийте дужки і зведіть подібні доданки: 179. а) 5(8 a + 9) + (4 a - 5); б) 2(5 b - 3 a) - (1,5 b - 2 a); в) -4(1,2 x + 1,5 y) + 4(1,2 х + 1); г) 2(2 х - 4 y) -3(2 х + 5 y + 2). 180. а) 3(4 х – 2 z) - (5 z + 10 x); б) –3(3 a + 1) - 5(a – 3 b). Спростіть вираз і знайдіть його значення: 181. а) 0,7(a - 10) + a - 5, якщо а = 3; б) -2,5 b - (11 - 1,5 b) + b, якщо b = 0,2; в) 2 x - 3(1 - y) + 4 y, якщо x = -2; y = 5. 182. а) 6 + 3(2 a - 4) – 8 a, якщо а = –1; б) 3(a + 6) - (a – 3 b) - 4 b, якщо а = 3, b = -3. Доведіть тотожність: 183. а) (a + b) - (a - b) = 2 b; б) 2 b × (-4) + 8 b - 4 = -4; в) 2 х - 1 - 5(1 - 2 х) = 12 х – 6; г) 2(3 а - 4) + 14 - 6 а = 6; д) a - (4 а - 3 b) = 3(b - a); е) 2 с = 12 с – 5(2 с + 3) + 15. 184. а) 2 b + 2(1 - b) = 2; б) 2 a - (1 + 2 a) + 1 = 0; в) 3 а - 6(3 - 2 а) = 3(5 а - 6); г) 2 х - 6 = - х - (7 - 3 х) + 1. 185. Ширина прямокутника дорівнює а см, а довжина на 3 см більша від ширини. Запишіть у вигляді виразу периметр прямокутника. 186.Довжина прямокутника дорівнює b см, а ширина на 5 см менша від довжини. Запишіть у вигляді виразу площу прямокутника. 187. На одній полиці стоїть n книжок, а на іншій ¾ у 1,5 разу більше. Скільки книжок на обох полицях? 188.На одній полиці стоїть k книжок, а на іншій ¾ на 12 книжок менше. Скільки книжок на обох полицях? 189. Один робітник виготовляє за годину с деталей, а інший ¾ на 2 деталі менше. Запишіть у вигляді виразу кількість деталей, які виготовлять за 8 год обидва робітники.
Запишіть у вигляді тотожності твердження: 190. а) Сума числа і протилежного йому числа дорівнює нулю; б) сума числа а й числа, протилежного числу b, дорівнює різниці чисел а та b; в) квадрат числа дорівнює квадрату модуля цього числа. 191. а) Добуток довільного числа і нуля дорівнює нулю; б) добуток двох чисел дорівнює добутку протилежних їм чисел; в) квадрат числа дорівнює квадрату протилежного йому числа. Спростіть вираз: 192. а) 2(3 с + 5) + 4(3 + 5 с) + 4 + 2 с; б) 0,2(х - 1) - 0,4(5 - 2 х) – 2,3; в) -(4 х + y + 3 z) + 3 y - 2(х - 3 z); г) д) 4(2(х + 2) - 4 х) + 2(х + 1); е) 5(m + 3(n - 1) - 1) - 5 m. 193. а) -(3 a - 6) + 3(2 - 2 a) + 15 a; б) 0,9(a - 3 b) - 0,2(5 b - 3 a) - 1,7 b; в) 4(5 n - 2(n - 1)) + 10; г) Доведіть тотожність: 194. а) 2(a + b + c) - (a + b - c) - (a - b + c) = 2(b + c); б) 28 + 2(2(2(b - 2) - 2) - 2) = 8 b. 195. а) 2(a - b - 1) - (a + b - 1) - (a - b + 1) = -2(b + 1); б) 1 - x - (1 - (1 - (1 - x))) = 0. Розв’яжіть рівняння: 196. а) 2(3 х –1) – 3(2 – х) = 1; б) 0,2(у - 2(у – 1) + 5) – 2 у + 3 = 0. 197. а) –3(1 – у) + 3(1 – 2 у) = 9; б) 2((х - 2) – 2(х – 1)) + 4 х = 1. 198. Перший лижник пробіг а м, другий ¾ на b м менше, ніж перший, а третій ¾ 1200 м. На скільки метрів менше пробіг другий лижник, ніж перший і третій разом? Запишіть результат у вигляді виразу. 199. На першій полиці є х книжок, а на другій ¾ удвічі більше, ніж на першій. З першої полиці забрали 10 книжок, а на другу поставили 3 книжки. Якою стала загальна кількість книжок на полицях? Запишіть результат у вигляді виразу.
200. Нехай m і n ¾ деякі натуральні числа. Доведіть, що: а) різниця чисел 11 m + 3 n і 7 m + 7 n ділиться на 4; б) сума чисел 10 m + 3 n + 2 і 2 m - 7 n + 6 ділиться на 4. 201. Доведіть, що сума трьох послідовних цілих чисел ділиться на 3. 202. Доведіть, щосума чотирьох послідовних цілих чисел не ділиться на 4. 203. Доведіть, що коли два цілі числа при діленні на 4 дають в остачі 2, то сума і різниця цих чисел діляться на 4. 204. Двоцифрове число, яке має а десятків і b одиниць, позначають через 205. Доведіть, що різниця числа 206. Доведіть, що коли два цілі числа при діленні на 3 дають рівні остачі, то різниця цих чисел ділиться на 3. Вправи для повторення 207. Обчисліть: а) 152 – 63; б) (1,22 – 1,84)3; в) Розв’яжіть рівняння: 208. а) (x -7)(х + 9) = 0; б) (2 х + 7)(3 x - 2) = 0; в) (7 - 3 х)(0,5 x - 1) = 0. 209. а) | х | = 5; б) | х + 5| = 2; в) |3 х + 9| = 0. 210. Сума трьох чисел дорівнює 10, до того ж, перше число на 20 менше, а третє ¾ на 15 більше, ніж друге. Знайдіть ці числа. 211*. Чоловік приїхав поїздом на станцію о 7 год 20 хв і пішки вирушив у село, розташоване у кількох кілометрах від станції. Йдучи зі сталою 212. З урни, в якій є чотири кулі, пронумерованих числами 1, 2, 3 і 4, навмання беруть дві кулі. Знайдіть імовірність того, що серед вибраних куль є куля з номером 1. 213. Використовуючи тричі цифру 3, знаки дій і за потреби дужки, складіть числовий вираз, значення якого дорівнює: а) 18; б) 9; в) 4; г) 81; д) 0.
Записуючи вирази, рівняння, нерівності, ми користуємося математичними символами «+», «–», «=», «<», «а 2» та багатьма іншими. Така єдина система умовних знаків, якою ми користуємося зараз, складалася в алгебрі поступово. Ще у ІІІ ст. давньогрецький математик Діофант замість слова «рівний» використовував окремий знак — букву і — першу букву слова isos, тобто рівний. Подібні скорочення використовували й інші математики, проте запропоновані ними символи не були загальновживаними. Створення сучасної символіки відбулось у XIV–XVIII ст. Значну роль у цьому процесі відіграв французький математик Франсуа Вієт, який уперше за допомогою символів почав записувати рівняння.
Найважливішим результатом наукової діяльності Ф. Вієта було те, що завдяки його працям алгебра стала наукою про алгебраїчні рівняння, яка ґрунтується на використанні символів (букв). Запитання і вправи для повторення § 2
214. Запишіть у вигляді виразу: а) різницю чисел 2,5 і а; б) куб числа с; в) подвоєну суму чисел а і b; г) суму квадратів чисел m і n; д) різницю числа а і добутку чисел b та с. 215. Автомобіль проїхав S км зі швидкістю 75 км/год. Скільки часу автомобіль був у дорозі? Запишіть результат у вигляді виразу. 216. Олівець коштує а к., а ручка ¾ b к. Запишіть у вигляді виразу вартість 2 олівців і 3 ручок. 217. Є дві ділянки прямокутної форми. Довжина і ширина першої ділянки відповідно дорівнюють m м і n м. Довжина другої ділянки на 5 м більша від довжини першої, а ширина на 2 м менша від ширини першої. Запишіть у вигляді виразу площу другої ділянки. Знайдіть значення цього виразу, якщо m = 50, n = 14. 218. Спростіть вираз: а) 6 а + 5(7 - 12 а); б) -3 х - 5(3 - 2 х) + 5 – 2 х; в) -4 + (5 х - y) - 4 х - (3 у + 5); г) 3 b + 7 - 2(3 - 2(b + 1)); д) 0,3(х - 4) - 0,4(х - у) + 1,6 у; е) 2,5(а - 2(b - 1) + 4) + 5 b. 219. Спростіть вираз і знайдіть його значення: а) 24(a - 2) - 4 a, якщо а = 0,05; б) 0,3(2 b - 3) + 3 - 4,6 b, якщо b = 0,5. 220. Знайдіть значення виразу2(x + 8) - 3(5 + х - y) + 7 y, якщо x = -6; y = 0,6. 221. Для яких значень х значення виразу 5 х – 8 дорівнює 1? 222. Доведіть, що значення виразу 2(1 – 3 х) – 3(1 – 2 х) не залежать від значень х. Доведіть тотожність: 223. а) 7(4 - а) - 3(-3 a + 1) - 25 = 2 a; б) 9,8 b - 5 = 9 b - 1,2 b - 2(2,5 - b); в) 4(n - 2) - 5(n - 1) = 3(n - 3) - 4(n - 1,5). 224. а) б) в) 225. Доведіть, що вираз 4(a + b + 2 c) - 3(a - b + c) - 2(- a + 2 b + c) тотожно рівний виразу 3(а + b + c). 226. За перший день магазин продав b кг цукру, за другий ¾ на 58 кг більше, ніж за перший, а за третій ¾ на 12 кг менше, ніж за другий. Запишіть у вигляді виразу кількість кілограмів цукру, проданого магазином за 3 дні. 227. У 7-А класі навчається n учнів, що на 5 учнів більше, ніж у 7-Б, і на 3 учні менше, ніж у 7-В. Запишіть у вигляді виразу кількість учнів у цих трьох класах разом. 228. З міста А в місто В виїхав мотоцикліст і рухався зі швидкістю 54 км/год. Через 0,5 год назустріч йому з міста В виїхав автомобіль і за t год зустрів мотоцикліста. Запишіть у вигляді виразу відстань між містами, якщо швидкість автомобіля дорівнює 72 км/год.
230. Запишіть формулу цілих чисел, які при діленні на 4 дають в остачі: 1; 3. 231*. Деякі три цілих числа при діленні на 3 дають різні остачі. Доведіть, що сума цих чисел ділиться на 3. 232. Знайдіть усі цифри а і b, для яких число Завдання для самоперевірки № 2 Рівень 1. Який із записів є виразом зі змінними? а) 2,5: 5; б) 3 х = 9; в) у > 3; г) 2 а + 3 аb. 2. Книжка коштує а грн., а зошит ¾ b грн. Запишіть у вигляді виразу вартість книжки і зошита разом. а) аb грн.; б) (а + b) грн.; в) (а - b) грн.; г) (b - а) грн. 3. Чому дорівнює значення виразу 2 x - 4, якщо x = -3? а) 10; б) -10; в) 2; г) -2. 4. Вкажіть вираз, тотожно рівний виразу 3 y + 5 - 7 y: а) у; б) 5 + 4 у; в) 5 - 4 у; г) 3 у - 2 у. 5. Спростіть вираз 4(5 а - 3 b) - (- b + 2 a) і вкажіть правильну відповідь: а) 18 a + 11 b; б) 22 a + 11 b; в) 18 a - 11 b; г) 22 a - 13 b. Рівень 1. Кілограм цукерок коштує а грн., а кілограм печива ¾ на b грн. менше. Запишіть у вигляді виразу вартість 1 кг печива й 1 кг цукерок разом. 2. Спростіть вираз 15 а - 0,4(5 а - 3) + 7. 3. Спростіть вираз 5(-4 х + 0,6) + 17,5 х - 4. Доведіть тотожність 3 с -(5 - 11 с) - 6 с + 5 = 8 с. Рівень 1. Розкрийте дужки і зведіть подібні доданки: 1,5(2 а - 4 b) - (2 - 3(2 b + a)). 2. Знайдіть значення виразу 25 х - 4(5 х - 3 у) - 2(5 + 3 х - y), якщо x = -7,6; y = 0,76. 3. У першій книжці є а сторінок, у другій ¾ на b сторінок менше, ніж у першій, а у третій ¾ удвічі більше сторінок, ніж у другій. Запишіть у вигляді виразу кількість сторінок у трьох книжках разом. 4. Доведіть, що вирази 0,3(а - 3) - 0,5(а - 1) і 0,2(а - 6) - 0,4(а - 2) є тотожно рівними. Рівень 1. Знайдіть значення виразу 2. На першій полиці стоїть а книжок, на другій — утричі більше, ніж на першій, а на третій — на 17 книжок менше, ніж на першій і другій полицях разом. Запишіть у вигляді виразу кількість книжок на трьох полицях разом. 3. Натуральне число а при діленні на 5 дає в остачі 4, а натуральне число b при діленні на 4 дає в остачі 2. Доведіть, що число 4 а + 5 b не кратне 10. 4. Доведіть, щосума трицифрового числа і подвоєної суми його цифр ділиться на 3.
ОДНОЧЛЕНИ
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 3530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.17.137 (0.011 с.) |

 .
. = - a + 25. ●
= - a + 25. ● - 2 +
- 2 +  = 3 a + b - 2. ●
= 3 a + b - 2. ● = 0.
= 0. Рівень А
Рівень А Рівень Б
Рівень Б (2 a - 7 b) -
(2 a - 7 b) - 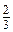 (3 b + a) + 2 a;
(3 b + a) + 2 a;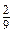 +
+  Рівень В
Рівень В . Отже,
. Отже,  ділиться на 11.
ділиться на 11. і суми його цифр ділиться на 9.
і суми його цифр ділиться на 9.
 Франсуа Вієт (1540–1603),
французький математик.
Першим увів єдину, послідовно проведену систему алгебраїчних символів
Франсуа Вієт (1540–1603),
французький математик.
Першим увів єдину, послідовно проведену систему алгебраїчних символів



 229. Три екскаватори вирили траншею. Перший екскаватор вирив х м траншеї, або
229. Три екскаватори вирили траншею. Перший екскаватор вирив х м траншеї, або  ділиться на 25.
ділиться на 25. і знайдіть його значення, якщо x = 0,8.
і знайдіть його значення, якщо x = 0,8. якщо а = 5.
якщо а = 5.


